7.2. Расчет параметров модели по методу наименьших квадратов (мнк)

Наибольшее распространение при решении задач оценивания параметров экспериментально-статистических моделей получил МНК (Гаусс, 1809г.).

В рамках МНК а ищется из условия минимизации функции:

(7.7)

Для моделей общего вида (7.3) МНК не имеет преимуществ перед другими методами типа (7.6). Вместе с тем, огромная популярность МНК определяется простотой нахождения оценок для весьма широкого класса моделей линейных по параметрам

, (7.8)

где

Для таких моделей приходим к задаче нахождения

(7.9)

Её решение получается из условий .

Чтобы записать решение в компактном виде, введём обозначения:

– вектор измерений выходной переменной у;

– матрица измерений входных переменных.

Тогда задача (4.9) запишется в виде

(7.10)

Из условия минимума можно получить систему уравнений

– т.н. информационная матрица Фишера), (7.11) решением которой находится вектор МНК – оценок параметров а.

(7.12)

Т.о., по МНК параметры модели (4.8) определяются путём решения системы алгебраических уравнений

(7.13)

где ,

причём

,

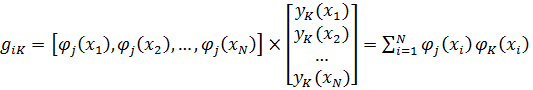(7.14)

7.3. Рекуррентная форма мнк

Из соотношений (7.12) – (7.14) следует, что для определения параметров моделей по МНК необходимо одновременно использовать все N замеров входных переменных . При организации расчётов на ЭВМ с ограниченной памятью такая вычислительная процедура оказывается неудобной для больших N, т.е. при обработке значительных массивов экспериментальной информации. В этом случае разумнее использовать рекуррентную вычислительную процедуру МНК, при которой уточнение оценки искомого вектора параметров модели происходит всякий раз после введения в память ЭВМ очередной экспериментальной информации о значении входных и выходных переменных . При этом очередная уточнённая оценка параметров формируется в соответствии и соотношениями

(7.15)

т.е. поправка к полученной на предшествующих i-1 шагах оценке пропорциональна ошибке прогноза выхода модели y, полученного на основе этой оценки.

В

(7.16)

ектор коррекции определяется по формуле:

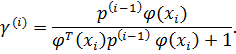
Здесь (7.17)

Где – обозначение единичной матрицы.

Исходными значениями для рекуррентного алгоритма служат и , где С – произвольное достаточно большое число.

В качестве положительной особенности рассмотренной вычислительной процедуры следует отметить отсутствие громоздкой операции обращения матриц

,

необходимой при использовании соотношения (7.13).

7.4. Экспериментально-статистические модели квазистационарных тп

Характерной чертой ТП в условиях реального производства является их квазистационарный характер. Будучи стабильными на достаточно длительных интервалах времени, технологические зависимости могут претерпевать существенные постепенные или внезапные изменения, причём, естественно, должны изменяться и параметры соответствующих экспериментально-статистических моделей. Например, параметры регрессионных моделей, определяющих зависимость подвижности бетонной смеси и прочность получаемого из неё бетона от рецептуры, могут скачкообразно изменяться при смене поставщика сырьевых материалов (цемента, гравия, песка) или даже при поступлении новой партии сырья от того же поставщика. Параметры аналогичных моделей прочности цемента могут медленно «дрейфовать» при изменениях свойств исходного сырья, происходящих вследствие постепенного перемещения фронта добычных работ на карьере.

Недостаток процедуры текущего оценивания параметров (7.15) – (7.17) для квазистационарных процессов заключается в медленной реакции на изменение их свойств. Минимизируя в каждый момент i сумму квадратичных невязок схема МНК придаёт равный вес как новым, так и старым измерениям. Если же требуется отслеживать меняющиеся параметры квазистационарного процесса, то новым измерениям необходимо придавать больше веса, нежели тем, что были получены ранее. Механизм «забывания прошлого» может быть введён различным образом. Используется, в частности, алгоритм текущего регрессионного анализа, в котором сумма квадратов ошибок оценивания минимизируется на текущем интервале, т.е.

(7.18)

Недостатком такого алгоритма оценивания является невозможность его записи в рекуррентной форме, подобной (7.15) – (7.17). Близок по смыслу, но лишен этого недостатка алгоритм МНК «с постепенным забыванием», минимизирующий взвешенную сумму квадратичных невязок:

(7.19)

причём (7.20)

При использовании данного алгоритма в рекуррентной форме оценки параметров рассчитывается по обычной формуле (7.15), однако вектор коррекции определяется с помощью модифицированных соотношений

(7.21)

где (7.22)

В модифицированном МНК «с постепенным забыванием» благодаря введению в правую часть (7.22) множителя , который всегда больше единицы, не происходит, как в обычном МНК, уменьшения с ростом i, а поэтому не стремятся к нулю и элементы вектора . Следовательно, возрастание невязки , вызванное изменением параметров , сразу же отразится не текущей оценке , что является достоинством модифицированного МНК.

Параметры рассмотренных алгоритмов «с забыванием» , определяющие «глубину памяти» или, другими словами, темп «забывания прошлого», выбираются исходя из априорных представлений о средней скорости дрейфа оцениваемых параметров модели ТП. Чем больше изменчивость параметров, тем выше темп «забывания» и тем меньше должны быть значения . С другой стороны, при выборе необходимо учитывать уровень случайных погрешностей контроля. Чем выше уровень измерительных шумов, тем осторожнее следует реагировать на текущую информацию, а следовательно, тем больше должны быть значения .