47

5. Методы оптимизации систем регулирования режима тп

В разделе 2.4 была рассмотрена схема двухуровневой оптимизации ТП. Она предусматривает оптимизацию режима ТП на верхнем уровне управления и стабилизацию «спущенного» сверху режима на нижнем уровне. В предыдущем разделе 4 была рассмотрена задача оптимизации режима. В данном разделе рассматривается задача стабилизации режима.

5.1. Типовые законы регулирования для управления многомерными объектами с перекрестными связями.

Методы пространства состояний, на основе которых решаются задачи среднеквадратичной оптимизации (а именно к таким задачам может быть, как было показано в разделе 2.4, сведена задача стабилизации ТП) плохо приспособлены для моделей технологических процессов с запаздыванием и, кроме того, они обычно приводят к алгоритмам, оценка которых с приемлемой точностью затруднена в условиях характерных для технологических процессов сильно зашумленных измерений. В этом плане более удобными нередко оказываются типовые законы регулирования, представляющие собой те ил иные частные случаи ПИД-регулятора. Вместе с тем, оптимальная настройка параметров регулятора с заданной структурой и, в частности, ПИД-регуляторов для многомерных систем с перекрестными связями представляет собой одну из трудных задач теории управления. И здесь вновь на помощь может прийти эвристика.

Рассмотрим задачу настройки многомерного регулятора, предназначенного для стабилизации многосвязного объекта с выходными переменными и управляющими воздействиями. Полагая, что каждое управляющее воздействие оказывает влияние на каждую выходную переменную, будем рассматривать линейную динамическую модель объекта управления

, , . (5.1)

Смысл задачи управления состоит в поддержании выходной переменной на заданном уровне в условиях неконтролируемых возмущающих воздействий . Будем также считать, что каждое управляющее воздействие формируется с учетом отклонений от задания каждой из выходных переменных по правилу

, , . (5.2)

Тогда уравнение «объект-регулятор», записанные в векторно-матричной форме, приобретут вид

, (5.3)

что соответствует блок-схеме, приведенной на рис. 5.1

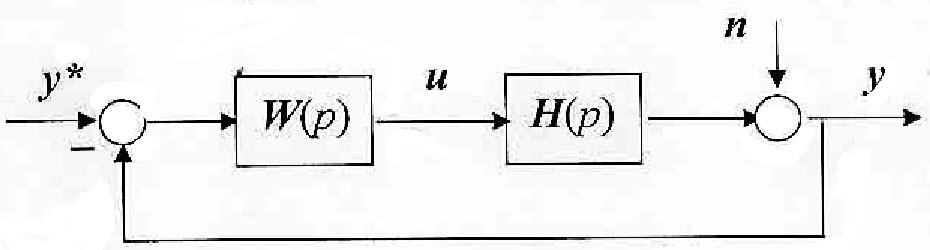
Рис. 5.1. Блок-схема системы управления.

Далее конкретизируем задачу, приняв, что динамика по каналам передачи управляющих воздействий описывается наиболее распространенной в промышленной автоматике моделью с запаздыванием

, , , , (5.4)

где и – соответственно устойчивые передаточные функции и запаздывания, определяющие динамическую модель управляемого процесса (см. рис. 5.2).

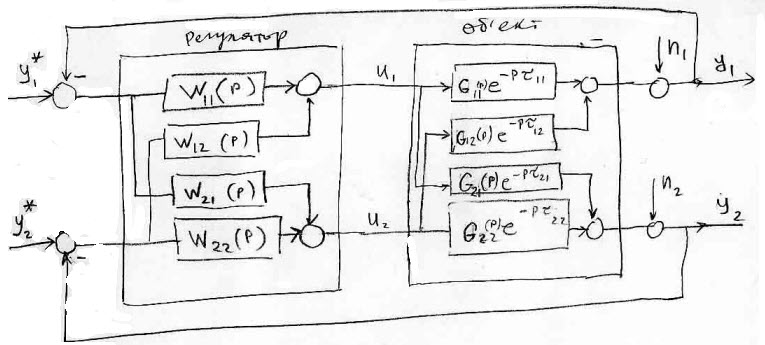
Рис. 5.2. Блок-схема многомерной системы управления (2 х 2)

Будем полагать, что для управления по отклонению используются ПИД-регуляторы

, , , (5.5)

и задача состоит в настройке их параметров , , . Если же интересует применение ПИ-регуляторов, то настройке подлежат параметры и , а параметры полагаются равными нулю. Заметим, что передаточная матрица многомерного типового регулятора может быть представлена в виде

, (5.6)

где , , – матрицы фигурирующих в (3.16) параметров П, И, и Д-составляющих, причем для ПИ-регулятора .

Рассмотрим наиболее важный в практическом отношении вариант, когда число управляющих воздействий равно числу стабилизируемых показателей, т.е. . Суть метода состоит в том, что вектор управляющих воздействий формируется в каждый момент времени в виде линейной комбинации двух составляющих, каждая из которых представляет собой выход “порождающего” (то есть соответствующего в той или иной мере упрощенной структуре объекта) многомерного типового регулятора. Подобная комбинированная структура позволяет сочетать быстроту реакции автономного по каналам управления регулятора первого типа с возможностью учета перекрестных связей более “осторожным” регулятором второго типа.

Сформируем закон управления в виде

, (5.7)

где и – передаточные матрицы вспомогательных типовых регуляторов, имеющих такую же структуру, что и передаточная матрица (5.5), а – подлежащий выбору весовой коэффициент, причем .

Диагональная передаточная матрица призвана стабилизировать объект , полученный из исходного пренебрежением перекрестными связями. Она составляется из передаточных функций автономных типовых регуляторов, причем их параметры могут быть, вообще говоря, определены по любой из известных схем расчета автономно работающих типовых регуляторов.

Передаточная матрица предназначена для стабилизации объекта, имеющего такую же матрицу статистических коэффициентов усиления, что исходный объект (5.5), но единую динамику по всем каналам управления, т.е.

. (5.8)

Запаздывание в (5.8) определяется по правилу

. (5.9)

Обозначим длительность переходного процесса при подаче ступенчатого управляющего воздействия . Выберем такую пару ( ), для которой

, . (5.10)

Тогда

, ( ) (5.11)

Формирование динамических характеристик вспомогательного объекта (5.8) по правилам (5.9) – (5.11) способствует (в духе робастного управления) повышению “осторожности” при формировании управляющих воздействий, так как объекты с большим запаздыванием и малой инерционностью требуют для стабилизации “слабых” настроек регуляторов.

Расчет параметров многомерного типового регулятора для объекта по методу динамической компенсации приводит к соотношениям

, (5.12)

где скалярные параметры , , для ПИД-регулятора или параметры , для ПИ-регулятора могут быть определены по любой из известных методик расчета типовых регуляторов применительно к одномерному объекту с единичным коэффициентом усиления (см. рис. 5.3).

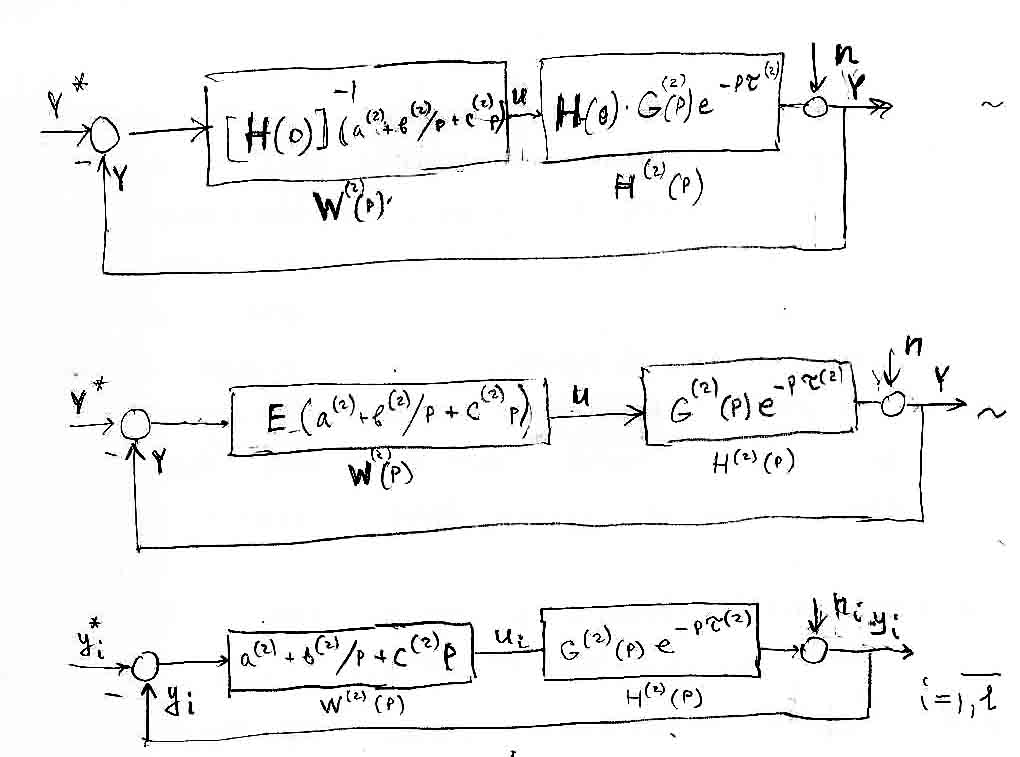
Рис. 5.3. Приведение многомерной задачи к одномерной для вспомогательного объекта

Конкретизируем намеченную схему расчета вспомогательных типовых регуляторов применительно к наиболее употребительной динамической модели инерционного звена с запаздыванием. В этом случае в (5.4)

, (5.13)

и для расчета одномерных типовых регуляторов можно использовать любой из известных методов расчета параметров одномерных типовых регуляторов для инерционных объектов первого порядка с запаздыванием. Матричная передаточная функция второго вспомогательного объекта в этом случае запишется в виде

. (5.14)

Динамические показатели в (5.14) определяются по правилу

, , , (5.15)

а параметры регулятора (5.12) рассчитываются по формулам любого из известных методов настройки одномерных типовых регуляторов.

Выбор и по правилу (5.15) соответствует минимизации коэффициентов усиления регулятора , и , что в свою очередь ведет к повышению “осторожности” при формировании управляющих воздействий.

Расчет весового коэффициента в комбинированном регуляторе (5.7) может быть выполнен с помощью так называемой матрицы Бристоля

, где , (5.16)

которая характеризует степень связности многомерного объекта. Руководствуясь тем, что данная матрица имеет тем большую диагональную доминантность, чем меньше влияние перекрестных связей, можно принять для расчета правило

, (5.17)

где , , .

В соответствии с этим правилом доля автономного регулятора во взвешенной сумме (5.7) тем выше, чем слабее перекрестные связи в объекте управления.

Рассчитав по предлагаемой схеме параметры вспомогательных регуляторов и , а также весовой коэффициент , можно полностью аналитическим способом найти все настройки многомерного типового регулятора.