7 Пример решения задач

Пример. Определить максимальные напряжения и перемещения консоли: стального равнобокого уголка. Левая полка нагружена равномерно распределенной по нормали нагрузкой, остальные грани свободны от механических нагрузок, как показано на рис. 1.

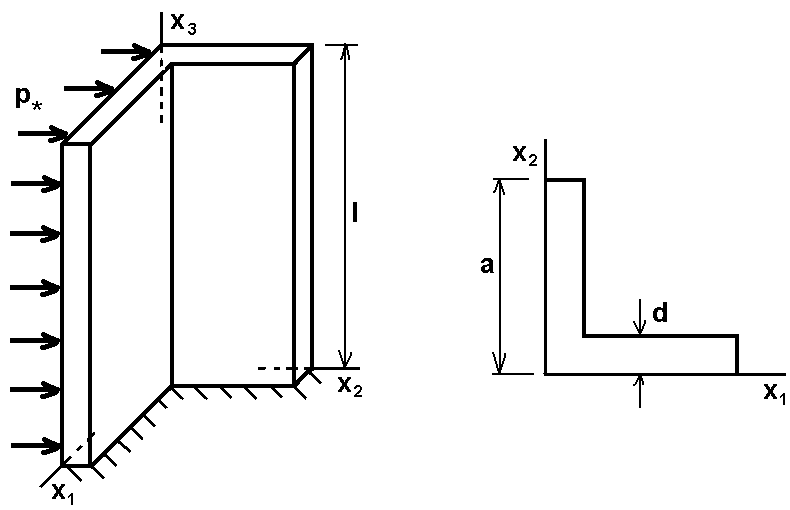
Рис. 1.

Постановка включает в себя уравнения равновесия (массовыми силами пренебрегаем)

,

закон Гука

,

геометрические соотношения Коши

.

Граничные условия формулируются для каждой грани. На нижней грани вектор перемещения равен нулю. На левой грани задан вектор напряжений

.

На остальных гранях вектор напряжения равен нулю.

Для решения задачи воспользуемся конечно-элементной программой FlexPDE.

Текст программы.

title 'Corner'

coordinates

cartesian3

select

painted { show color-filled contours }

variables

U { X displacement }

V { Y displacement }

W { Z displacement }

definitions

a = 5E-2

d = 1E-2

l = 2E-1

p_0=0.5E6

k=1E2

E=2.1E11 { Youngs modulus }

nu=0.31 { Poisson's Ratio }

{ define the constitutive relations }

lam=E*nu/(1-2*nu)/(1+nu)

mu=E/2/(1+nu)

{ Strains }

S11 = dx(U)

S22 = dy(V)

S33 = dz(W)

S12 =( dy(U) + dx(V))/2

S23 = (dz(V) + dy(W))/2

S13 = (dx(W) + dz(U))/2

{ Stresses }

T11 = lam*(S11+S22+S33)+2*mu*S11

T22 = lam*(S11+S22+S33)+2*mu*S22

T33 = lam*(S11+S22+S33)+2*mu*S33

T12=2*mu*S12

T13=2*mu*S13

T23=2*mu*S23

initial values

U = 1.e-5

V = 1.e-5

W = 1.e-5

equations

U: dx(T11) + dy(T12) + dz(T13) = 0 { the U-displacement equation }

V: dx(T12) + dy(T22) + dz(T23) = 0 { the V-displacement equation }

W: dx(T13) + dy(T23) + dz(T33) = 0 { the W-displacement equation }

extrusion z = 0,l

boundaries

surface 1 value(U)=0 value(V)=0 value(W)=0

surface 2 load(U)=0 load(V)=0 load(W)=0

Region 1

start(0,0)

load(U)=0 load(V)=p_0 load(W)=0

line to (a,0)

load(U)=0 load(V)=0 load(W)=0

line to (a,d)

to (d,d)

to (d,a)

to (0,a)

to close

monitors

grid(x+k*U,y+k*V,z+k*W) as "Shape"

plots

grid(x+k*U,y+k*V,z+k*W) as "Shape"

grid(x+k*U,y+k*V) on z=l as "Shape"

contour(U) on z=l as "X-displacement"

contour(V) on z=l as "Y-displacement"

contour(T11) on z=0 as "X-stress"

contour(T22) on z=0 as "Y-stress"

contour(T33) on z=0 as "Z-stress"

contour(T12) on z=0 as "XY-stress"

contour(T13) on z=0 as "XZ-stress"

contour(T23) on z=0 as "YZ-stress"

end

Анализ расчетов показывает, что наибольшие нормальные напряжения возникают в области заделки. На рис. 2 приводится поле нормальных напряжений . Уголок испытывает косой изгиб, что отчетливо видно из трехмерной картины деформированного состояния уголка, представленной на рис. 3. На рис. 4. показан верхний торец уголка в деформированном состоянии. Видно, что сечение мало деформируется (в силу достаточно толстых стенок), а только поворачивается.

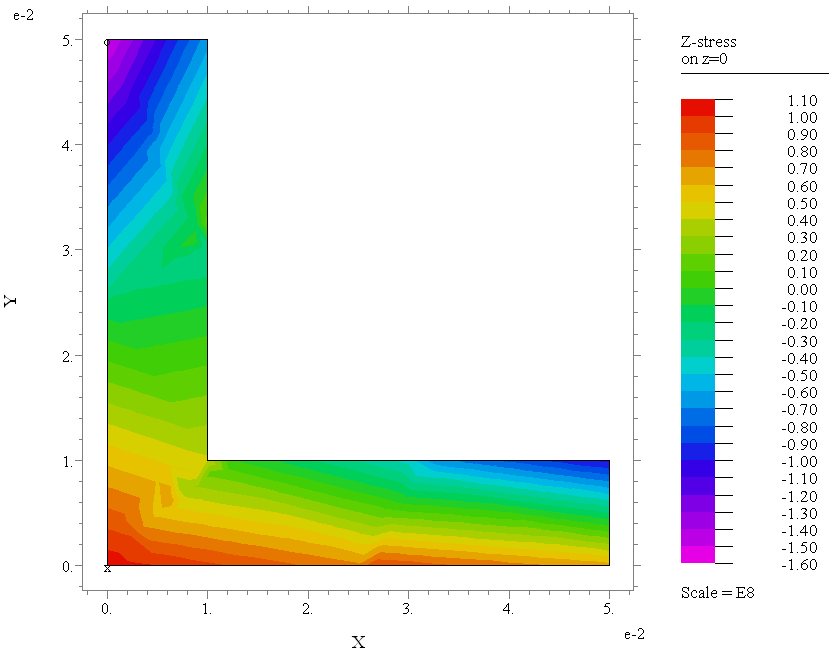
Рис. 2.

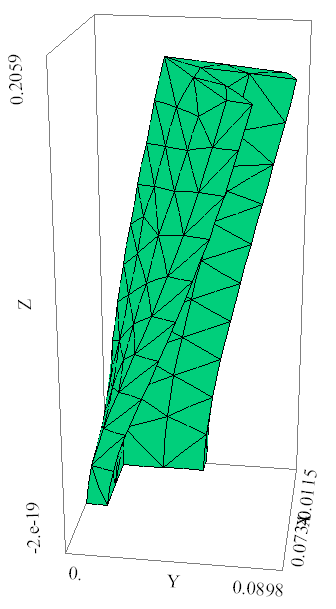
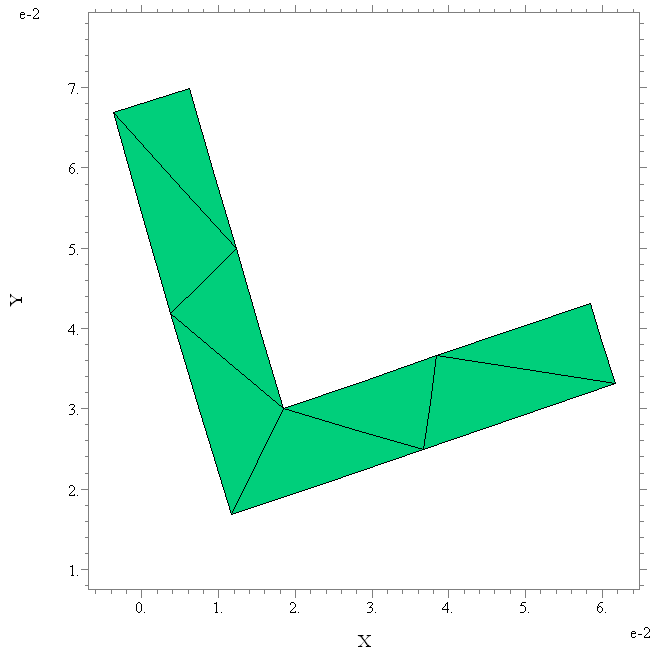
Рис. 3. Рис. 4.

ЗАКЛЮЧЕНИЕ

В учебном пособии приведены основные формула механики сплошной среды. Приводятся основы термодинамики. На основании положений термодинамики необратимых процессов дается систематический подход вывода определяющих соотношений для жидких, твердых и газообразных сред. Подробно разбираются постановки задач в этих средах. Приведено численное решение с помощью конечно-элементной программы (текст программного кода приводится) одной трехмерной задачи теории упругости. Такой подход служит базовым при решении подобных проблем. Анализ решений поможет в тренировке инженерной интуиции.

СПИСОК ЛИТЕРАТУРЫ

1. Победря Б.Е., Георгиевский Д.В. Основы механики сплошной среды. Курс лекций. М., ФИЗМАТЛИТ, 2006. – 272 с.

2. Можен М. Механика электромагнитных сплошных сред. М., Мир, 1991. – 560 с.

3. Пригожин И. Введение в термодинамику необратимых процессов. Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. – 160 с.

4. Дьярмати И. Неравновесная термодинамика. М., Мир, 1974. – 304 с.

5. Полторак О.М. Термодинамика в физической химии. М., Высш. шк. 1991. – 319 с.

6. Базаров И.П. Термодинамика. М., Высш. шк. 1991. – 376 с.

7. Румер Ю.Б., Рывкин М.Ш. Термодинамика, статистическая физика и кинетика. М., Москва, 1977. – 552 с.

8. Амензаде Ю.А. Теория упругости. М., Высшая школа, 1976. - 272 с.

9. Снеддон И.Н., Бери Д.С. Классическая теория упругости. М., Гос. изд. физ.-мат. литературы, 1961. - 220 с.

10. Тимошенко С.П., Гудьер Дж. Теория упругости. М., Наука, 1875. – 576 с.

11. Новацкий В. Теория упругости. М., Мир, 1975. - 872 с.

12. Хан Х. Теория упругости. М., Мир, 1988. – 344 с.

13. Голубева О.В. Курс механики сплошных сред. М., высшая школа, 1972. – 368 с.

38