3 Модель идеальной жидкости
Получим дифференциальную форму уравнения сохранения энергии (2.8). Перепишем это уравнение в виде
Применим теорему Гаусса – Остроградского, и перейдем к интегрированию по объему
.
Группа слагаемых, стоящих в круглых скобках обращается в нуль в силу выполнения уравнения движения сплошной среды. Далее из условия произвольности объема следует
. (3.1)
Это уравнение закона сохранения энергии в дифференциальной форме будет использоваться для построения определяющих соотношений. Основой дальнейших исследований является правило задания выражения внутренней энергии. А это выражение тесно связано с конкретной средой. Так, если рассматривается упругое тело, то энергия, которая может накапливаться в теле, зависит от внешнего параметра деформации. Если рассматривается жидкость, то энергия, накапливаемая в теле, будет связана со сжатием среды, внешним параметром такого сжатия является объем. Однако вместо объема удобно ввести относительную величину – объем, отнесенный к массе. Такой величиной является величина, обратная плотности. Тогда можем рассматривать термодинамическую функцию внутренней энергии как функцию энтропии и обратной величины плотности
.
Найдем производную по времени
.
Подставляя это соотношение в (3.1), получим
,
где
- тензор скоростей деформации.
Пусть рассматривается изоэнтропический и адиабатический процесс. Для них выполняются следующие соотношения
.
Тогда предыдущее равенство принимает вид
. (3.2)
Продифференцируем
по времени и воспользуемся уравнением
неразрывности (1.1), тогда эту производную
можно записать в следующем виде
.
Подставляя это соотношение в (3.2), получаем
,
В силу произвольности тензора скоростей деформации, получаем, что оба выражения должны быть одного вида. Это возможно в случае, когда
. (3.3)
- называется
термодинамическим
давлением.
Тогда
и предыдущее соотношение приобретает вид
.
А в силу произвольности тензора скоростей деформаций
. (3.4)
Соотношения (3.3) являются определяющими соот6ношениями для идеальной жидкости в предположении адиабатического и изэнтропического процесса. Термодинамическое давление находится по (3.4) при условии, что задана термодинамическая функция внутренней энергии.
4 Модель вязкой жидкости
Термодинамическую функцию внутренней энергии, как и в предыдущем случае, представляем в виде
.
Используем также дифференциальную форму закона сохранения энергии (3.1), который в предположении характера рассматриваемого процесса можно записать в виде
. (4.1)
Т.к. для вязких жидкостей имеют место необратимые процессы, то наравне с законом сохранения энергии будем использовать неравенство Клаузиуса-Дюгема (2.12)
,
которое преобразуем к дифференциальной форме
. (4.2)
Выразим из (4.1) функцию мощности внутреннего источника тепла и подставим полученное в (4.2)
.
Откуда после очевидных упрощений и представления напряжений в виде суммы обратимой и необратимой частей
,
получаем
.
Далее находим производную по времени от внутренней энергии
,
используем уравнение неразрывности и подставляем в предыдущее неравенство
.
Левая часть этого
неравенства определяет количество
энергии, рассеиваемой в единице объема
в единицу времени в жидкой среде, в
которой происходят неравновесные
процессы. С другой стороны рассеянная
энергия в точности равна производству
энтропии, т.е. возникновению энтропии
за единицу времени в единице объема,
причем из неравенства Клаузиуса-Дюгема
следует, что производство энтропии
всегда является положительно определенной
величиной. Обозначая производство
энтропии
,
предыдущее неравенство перепишем в
виде
.
Производство энтропии носит также название функции скорости диссипации и характеризует в данной системе источники энтропии, которые могут иметь различную природу. Фактически они представляют собой механизмы потерь или, другими словами, описывают физическую сущность путей рассеивания или отвода энергии из системы. В итоге, так или иначе, они связаны с передачей тепла в окружающую среду. Поэтому при изучении необратимых процессов в жидкости наиболее полная постановка задачи включает в себя формулировку основных факторов механических или иных механизмов потерь, которые неизбежно связаны с изменением температуры. Все это, как легко видеть, напрямую связано с заданием функции . При построении этой функции следует руководствоваться некоторых правил, основным из которых является малое отклонение системы от равновесного состояния. Так при термодинамическом равновесии производство энтропии равно нулю. В неравновесных термодинамических процессах, когда имеются малые отклонения от равновесного состояния, производство энтропии можно представить в виде линейного приближения по скоростям независимых параметров и градиенту температуры в виде следующих кинематических линейных комбинаций
.
Функции
называются диссипативными потоками
или обобщенными диссипативными силами
и должны обеспечивать выполнение
неравенства скорости диссипации. Функции
могут зависеть от параметров
термодинамической системы, их скоростей
и градиента температуры, т.е. от параметров
.
Сравнивая это представление с предыдущим
соотношением, получаем
Учитывая независимость скоростей внешних и внутренних параметров, получаем систему равенств
,
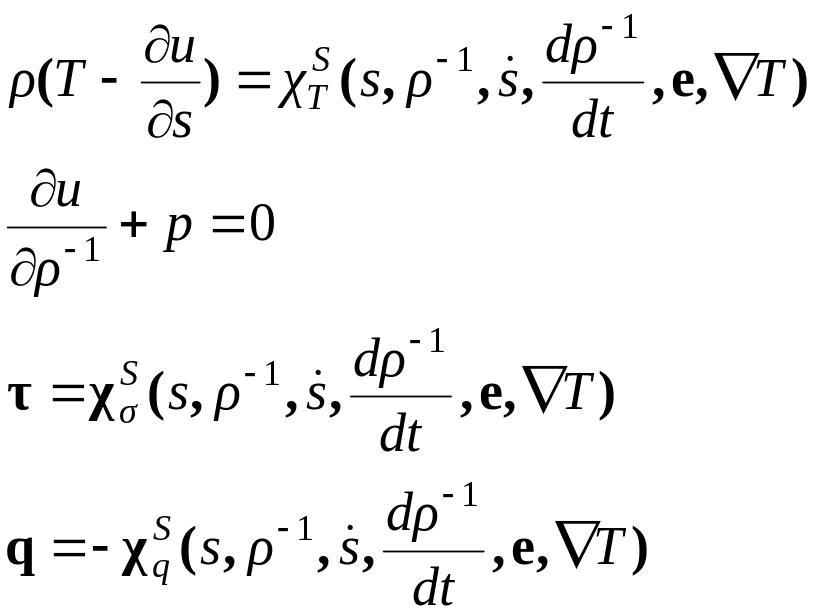которые можно переписать в виде
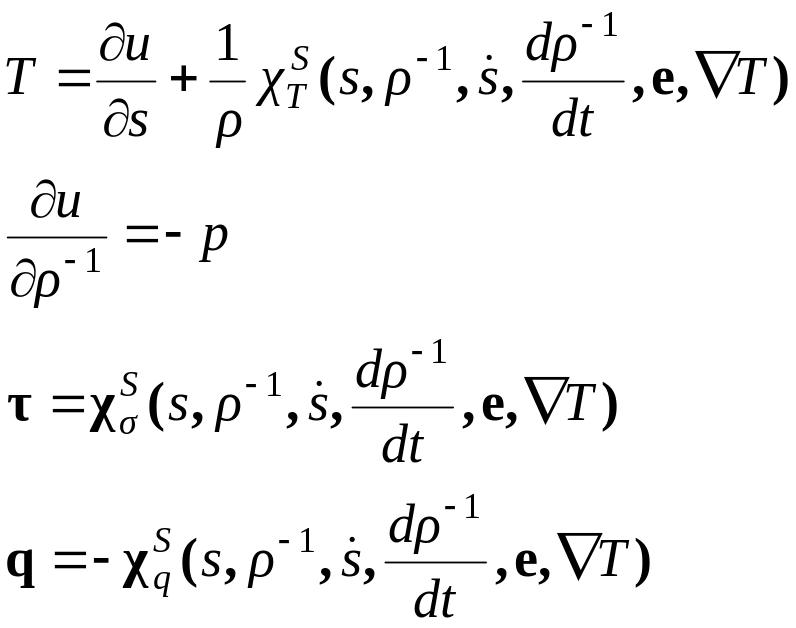, (4.3)
которые носят название определяющих соотношений. Таким образом, для получения определяющих соотношений вязкой жидкости необходимо конкретизировать набор параметров состояния и построить две функции: функцию внутренней энергии и функцию скорости диссипации , руководствуясь при этом физическими представлениями о свойствах рассматриваемой среды.
Для модели вязкой жидкости возьмем функцию диссипации в виде
, (4.4)
где положили
.
Остальные потоки будем считать зависящими
только от тензора скоростей деформации
и градиента температуры соответственно.
Считая, как это отмечалось ранее, что
система мало отклоняется от положения
термодинамического равновесия, можем
представить эти функции в виде линейной
комбинации от их параметров, т.е. записать
в виде
,
которые носят название соотношений Онзагера. Подставим эти разложения в (4.4), получим квадратичную форму относительно компонент тензора скорости деформации и вектора градиента температуры
,
которая должна быть положительно определенной. Условия положительной определенности критерия Сильвестра позволяют сделать заключения о независимом количестве компонент этих тензоров.
Обращаясь к определяющим соотношениям (4.3), можем их записать в виде
.
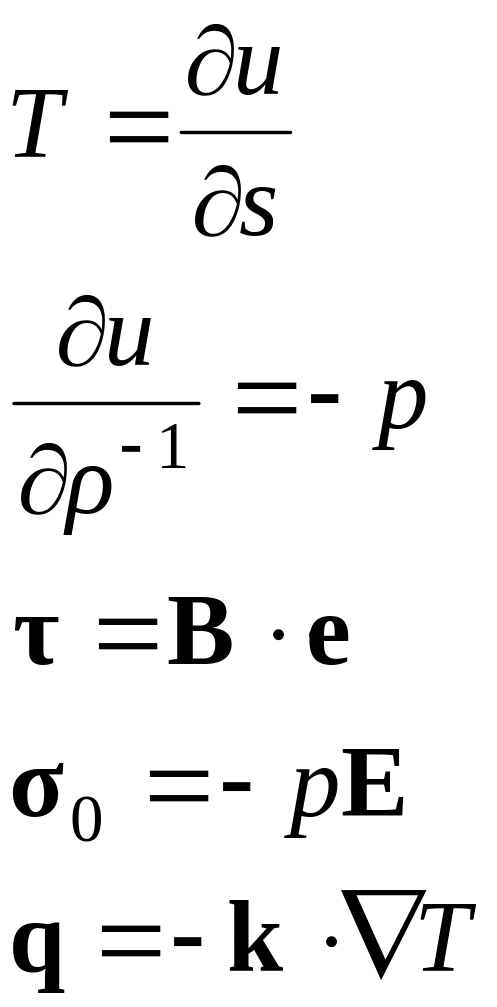Тензор
носит названия тензора вязких напряжений.
В частном случае изоэнтропического и
адиабатического процесса определяющие
соотношения принимают вид
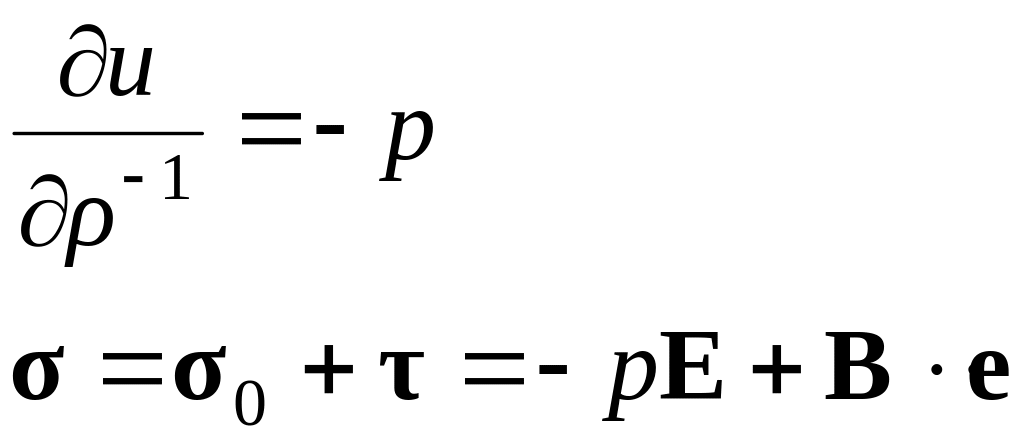. (4.5)