2.2 Термические и калорические уравнения

Для равновесных внутренних параметров , в силу их зависимости от внешних параметров и от температуры , должно выполняться соотношение

. (2.1)

Если внутренним параметром является внутренняя энергия , то

. (2.2)

Если эти уравнения известны, то (2.1) называется термическим уравнением, а (2.2) калорическим.

Пример 1. Калорическое уравнение идеального газа. Рассматривается идеальный газ. Одним внешним параметром является его объем. Тогда калорическое уравнение принимает вид

Выберем некоторое состояние и разложим функцию, стоящую справа, в ряд Тейлора, ограничиваясь только первыми слагаемыми

По закону Джоуля о независимости внутренней энергии газа от его объема при постоянной температуре, получаем, что

.

Вводя удельную теплоемкость при постоянном объеме

,

получаем приращение внутренней энергии за счет повышения температуры

. (2.3)

Пример 2 термического уравнения идеального газа. Уравнение Клайперона-Менделеева является примером термического уравнения идеального газа

,

где - число молей газа массой , - молярная масса, Дж/(К моль). Это уравнение можно переписать в другой форме

, (2.4)

которое часто используется в гидродинамике.

В настоящее время известно более 150 термических уравнений состояния реальных газов, среди которых можно упомянуть уравнение Ван-дер-Ваальса

,

первое и второе уравнения Дейтеричи,

,

второе уравнение Дейтеричи

,

уравнение Бертло

,

вириальную форму уравнения состояния

,

уравнение Майера-Боголюбова и другие.

2.3 Первое начало термодинамики применительно к сплошным средам

Первое начало термодинамики и основанный на нем способ определения внутренней энергии системы были открыты при попытках описать явления, сопровождающие совместное протекание процессов теплообмена и совершение работы различного рода. Внутренняя энергия системы является однозначной функцией ее состояния и изменяется под влиянием внешних воздействий. Для элементарного процесса перехода системы из одного равновесного состояния в другое всегда выполняется соотношение

. (2.5)

Закон сохранения, записанный в виде (2.5), - это новый закон физики, отличающийся от своих частных формулировок в механике и теории электричества. Он основан на опытных данных о сохранении алгебраической суммы при различных способах перехода от одного состояния макроскопической системы к другой. Величины имеют одинаковую размерность – размерность энергии, но обладают существенно различными физическими и математическими свойствами. Из уравнения (2.5) легко получить частные случаи, когда изменение энергии системы проявляется в виде работы только одного рода или в форме теплоты. Впервые он был установлен в механике для систем, для которых можно не учитывать теплообмен и обобщенные формы работы и достаточно рассмотреть только механическую энергию – кинетическую и потенциальную. Закон сохранения энергии был сформулирован также в макроскопической теории электричества, когда ни теплообмен, ни механическая энергия не играют роли, но учитываются электрическая и магнитная составляющие. Появление исследований о переходах одних видов энергии в другие позволило взять в качестве универсальной меры протекающих процессов энергию и сформулировать наиболее общую форму закона сохранения энергии для взаимосвязанных процессов механической, тепловой и электромагнитной природы.

Заметим, что первое начало термодинамики относится к равновесным процессам, так как описывает баланс между приращением внутренней энергии, с одной стороны, и тем количеством энергии, которым обменивается система с окружающей средой в виде работы и теплоты. Легко видеть, время нигде в выражение этого закона не входит. Однако в механике сплошных сред рассматриваются движения частиц, и говорить о равновесии уже не приходится. Поэтому закон сохранения энергии обобщается на термодинамику неравновесных процессов, при условии, что эти процессы протекают так, что их параметры мало отклоняются от некоторого равновесного состояния. Математически это означает, что разложения термодинамических функций в окрестности некоторого равновесного состояния осуществляется только до членов первого порядка малости.

Получим интегральную форму закона сохранения энергии применительно к такой термодинамической системе, какой является сплошная среда.

Пусть рассматриваемая система может обмениваться с окружающей средой энергией в виде работы. Выделим в СС в текущей конфигурации произвольный объем , ограниченный поверхностью . Рассмотрим баланс кинетической энергии, для чего следим за движущимся объемом, содержащем одни и те же частицы среды. Умножим скалярно уравнение (1.2) на поле скоростей

.

Преобразуем выражения, стоящие под знаком интеграла, получим теорему об изменении кинетической энергии

.

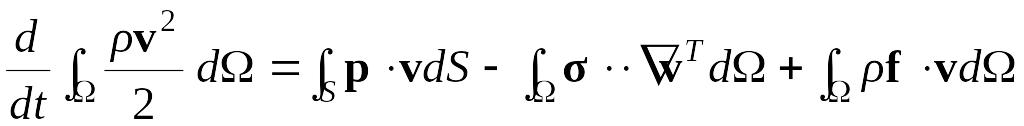Скорость изменения кинетической энергии равна сумме полных мощностей внутренних, массовых и поверхностных сил.

Здесь - кинетическая энергия системы; - полная мощность внутренних сил; - полная мощность массовых сил; -полная мощность поверхностных сил.

Рассмотрим работу, совершаемую поверхностными и массовыми силами над данной системой

.

Тогда, работа, которую совершает система над окружающими телами

.

А приток тепла в рассматриваемый объем

.

Эксперименты показывают, что для всех термодинамических процессов, связывающих некоторое начальное состояние при и некоторое конечное состояние при , интеграл

(2.6)

имеет одно и то же значение, хотя интегралы и по отдельности зависят не только от состояний системы при и , но также и от конкретного процесса, связывающего эти два состояния. Кроме того, интеграл (2.6) пропорционален массе системы. эти экспериментальные наблюдения позволяют заключить, что существует экстенсивный параметр состояния , называемый полной энергией системы, такой что

. (2.7)

Это соотношение есть математическое выражение первого начала термодинамики. Разность

.

Подставляя в (2.7) интегральные выражения мощностей и энергий, получаем

. (2.8)

Скорость изменения полной энергии равна сумме мощностей внешних сил плюс скорость притока тепла через поверхность и плюс мощность внутренних источников тепла.