4.2.3 Нестационарная теплопроводность плоской стенки

Процессы переноса тепла являются одним из основных разделов современной науки и имеют большой практическое значение в стационарной и промышленной энергетике, в технологических процессах, химической, строительной, лёгкой и других отраслей промышленности. Например, расчёт тепловых аппаратов, работающих при нестандартном режиме, расчёт теплоизоляции зданий, печей, трубопроводов, нагревание машин и др. Исследование кинетики процессов сорбции, сушки, горения и других химико-технологичеких процессов связано с решением задач диффузии, которые аналогичны задачам нестандартной теплопроводимости.

Если температуре поле меняется во времени, то тепловые процессы, протекающие в таких условиях, называют нестандартными.

Нестационарные процессы теплопроводимости встречаются при охлаждении металлических заготовок, прокаливании твёрдых тел, в производстве стекла, общие кирпича, нагревании дерева, вулканизации резины и т.п.

Теплоту при нестационарном режиме можно определить, если найти закон изменения температуры и теплового потока во времени и в пространстве; т.е.

и

где x, y,z – координаты точки;

τ – время.

Указанные зависимости могут быть найдены из решения дифференциального уравнения теплопроводимости Фурье:

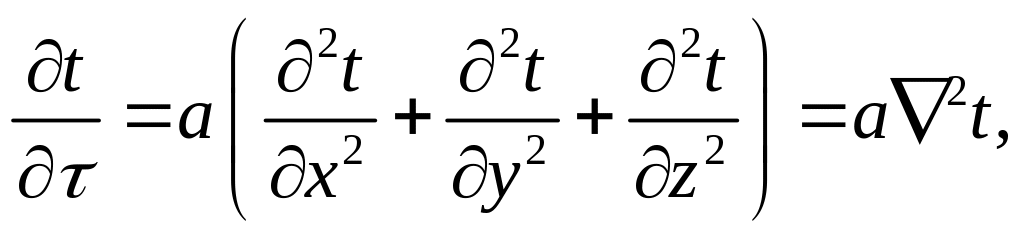(4.24)

где а – коэффициент температуропроводимости, определяемый по формуле

(4.25)

(Здесь – удельная теплоёмкость твёрдого тела; ρ – плотность материала стенки; - оператор Лапласа; - температура).

При решении уравнения (4.24) необходимо задавать граничные условия и начальное распределение температуры в теле (краевые условия).

Граничные условия задаются уравнением вида

(4.26)

где - температурный градиент на поверхности;

α – коэффициент теплоотдачи между жидкой средой и поверхностью твёрдого тела;

λ_ст – коэффициент теплопроводности стенки;

t_ст - температура поверхности стенки;

t_ср – температура окружающей среды.

Физические параметры λ, с, ρ считаются постоянными. Температура рассматриваемого тела в начальный момент времени при τ=0 распределена равномерно, т.е. . Это может быть температура газов, жидкости, омывающих стенку плоской пластины, цилиндра или шара.

Решение уравнений (4.24) и (4.26) с учётом граничных и временных условий даёт уравнение температурного поля вида

(4.27)

Из уравнения (4.27) видно, что температура зависит от большого числа переменных и постоянных параметров и решение его представляет сложную математическую задачу.

Используя теорию подобия и метод размерностей, можно переменные величины сгруппировать в три безразмерных комплекса:

- критерий Био;

- критерий Фурье; (4.28)

- безразмерная координата,

– характерный размер тела.

Тогда искомая температура в виде безразмерного комплекса может быть представлена следующим уравнением

(4.29)

где – избыточная температура пластины (стенки), равная

(t – текущее значение температуры стенки;

– начальная температура окружающей среды);

(4.30)

разница между начальной температурой стенки и температурой окружающей среды.

Таким образом, температура поверхности стенки цилиндра определяется из соотношения (4.29)

, (4.31)

где – температура в центре пластины, цилиндра, шара.

Количество теплоты, которое отдаёт (или воспринимает) пластина за время τ, должно равняться изменению её внутренней энергии за период полного её охлаждения (нагревания).

Начальная внутренняя энергия пластины, отсчитанная от внутренней энергии при температуре среды, окружающей стенку, как от нуля, равна

(4.32)

При использовании безразмерных комплексов (критериев Bi и F₀) количество теплоты, выделившейся при охлаждении пластины, равно

(4.33)

или

(4.34)

где Q_τ – количество теплоты, переданное в окружающую среду за время τ;

t_cp.ст. – средняя температура стенки по истечении периода времени τ.

Зависимости (4.31), (4.32), (4.33) даются в виде таблиц или в виде графиков (рисунки 4.4, 4.5, 4.6, 4.7, 4.8).

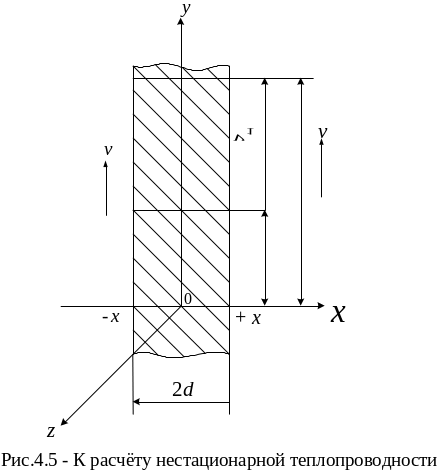
Порядок определения температуры на поверхности тела и в его центре.

Рассмотрим охлаждение плоскопараллельной пластины толщиной 2 δ ( ). Размер пластины в направлении осей O_y и O_z бесконечно велики. Пластина омывается с обеих сторон жидкостью или газом с постоянной температурой t_cp, причём коэффициент теплопередачи α, для обеих поверхностей имеет одинаковое и постоянное значение.

В начальный момент времени пластина имеет во всех своих точках постоянную температуру t₀, поэтому и избыточная температура v₁=t₀-t_cp будет также постоянной для всех точек тела. Кроме того, заданы коэффициент теплопроводности λ_ст, плотность тела ρ_ст и теплоёмкость его с_ст , величины которых полагаются постоянными.

Порядок определения температуры на поверхности тела и в центре его следующий.

1. Определяют критерий Bi и F₀ по формулам (4.28).

2. По специальным таблицам (табл. 4.3, 4.4, 4.5) определяют относительные (безразмерные) температуры 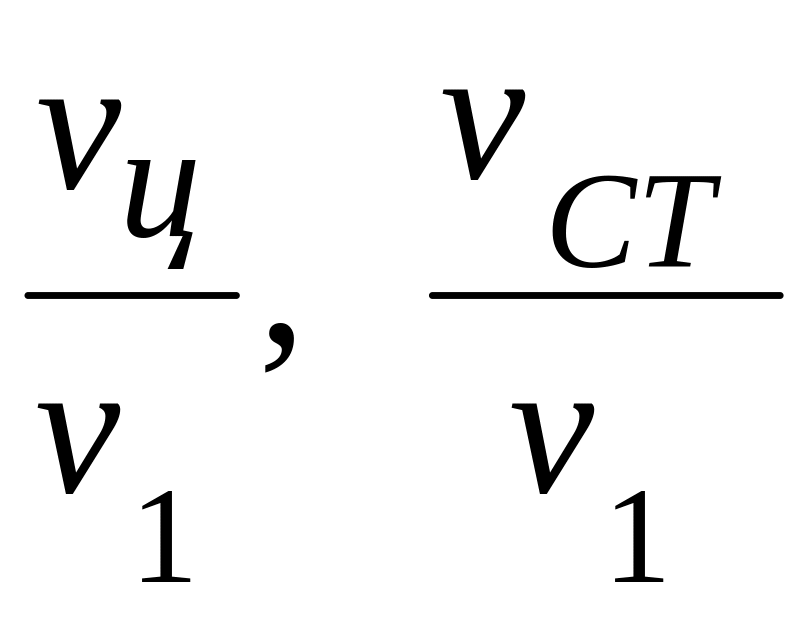и безразмерную теплоту Q_τ/Q₀.

3. Поскольку начальные значения t₁, t_cp и начальная теплота Q₀ известны, то по формулам 4.30, 4.31 и 4.33 определяют значения температур:

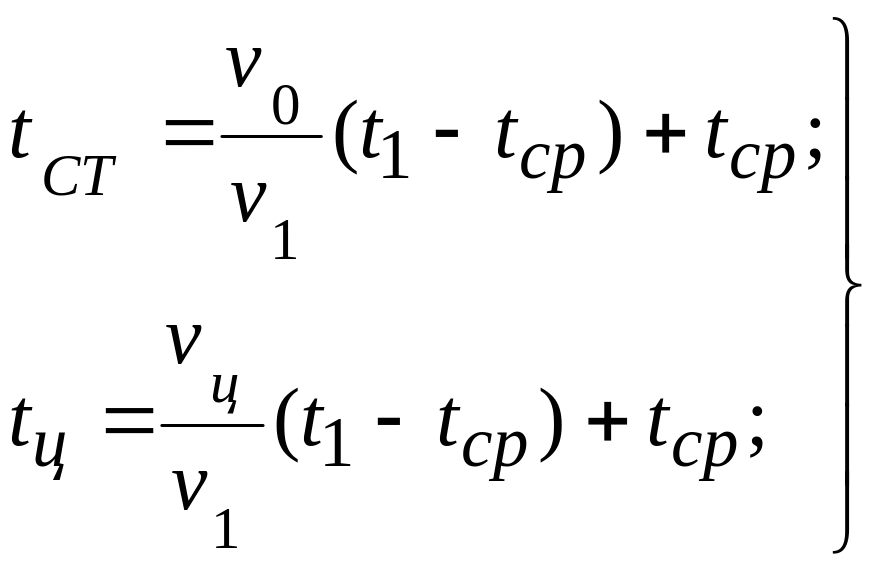(4.35)

и величину тепла Q_τ.

Аналогично определяются температура t_ст, t_ц, Q_τ для бесконечного цилиндра и шара. Однако в качестве характерного размера в системе уравнений (4.28) принимается радиус цилиндра (шара), т.е.

и (4.36)

Безразмерные температуры и безразмерные величины тепла цилиндра и шара даны в табл. 4.6, 4.7, 4.8.

Пример 4.2. Определить температуру на поверхности и в центре равномерно нагретого до t₁=927°C длинного стального цилиндра диаметром d_ц равным 400 мм через 0,5 часа и через 1,0 час после помещения его на воздухе с температурой 27°C. Коэффициент теплоотдачи от стенки, цилиндра к воздуху α=50 Вт/м²∙К, коэффициент теплопроводимости стали λ_ст=50 Вт/м∙К, плотность стали ρ_ст=7900 кг/м³.

Решение

1. Определим температуры поверхности t_ст и центра t_ц, спустя 0,5 ч после пребывания цилиндра на воздухе:

   1. коэффициент температуропроводимости

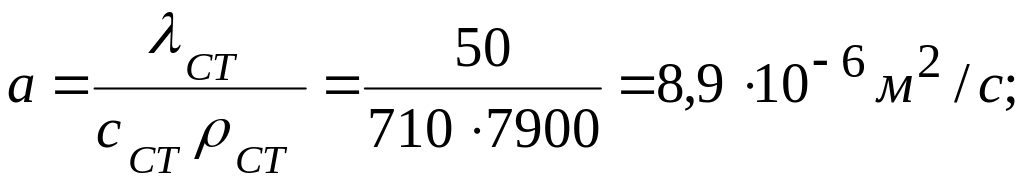
2. критерий Фурье

3. критерий Био

4. По табл. 4.7, 4.6 находим безразмерные температуры при известных критериях Био и Фурье

5. температура поверхности цилиндра определяется по формуле (4.35)

;

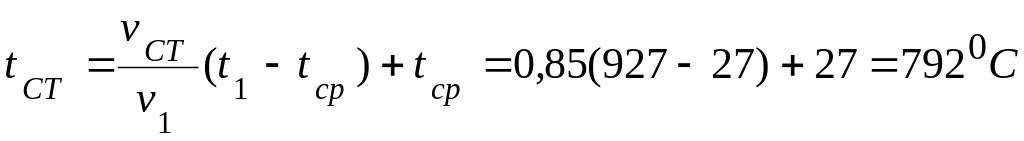6. температура в центре цилиндра

;

7. потери тепла цилиндра за 0,5 ч по табл. 4.8.

т.е. цилиндр потерял 13% от своей начальной внутренней энергии.

2. Определим температуры поверхности t_ст и центра t_ц спустя 1,0 ч после пребывания цилиндра на воздухе:

   1. критерий Фурье

Критерий Био остаётся неизменным.

2. по значениям критериев Bi и F₀ из табл. 4.7 и 4.6 находим безразмерные температуры

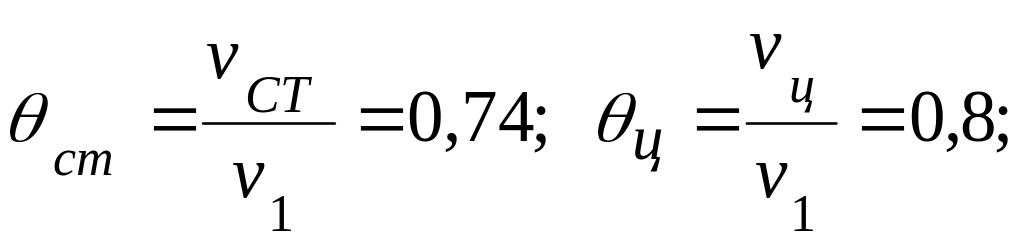
3. температура поверхности цилиндра

4. температура в центре цилиндра

;

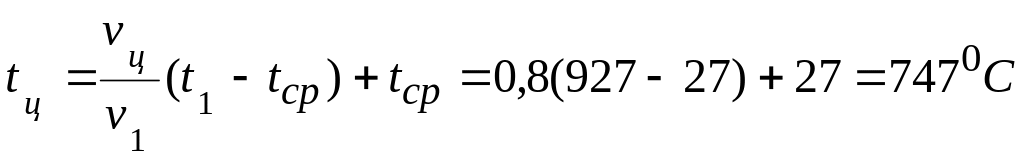5. потери тепла цилиндра за 1 ч. по табл. 4.8

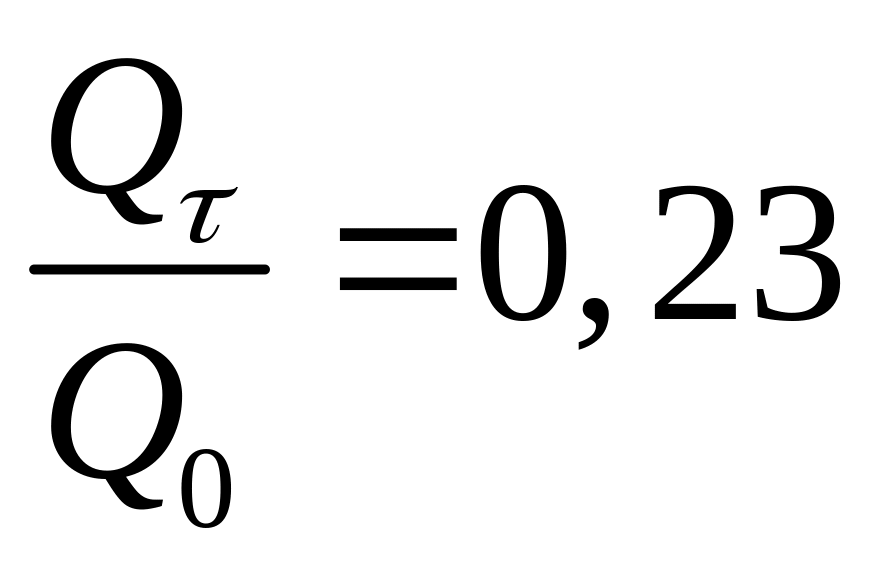6. , т.е. цилиндр потерял 23% тепла от своей начальной внутренней энергии.

На основании расчётных данных можно построить поле распределения температур по времени и пространству, как показано на рис. 4.6.

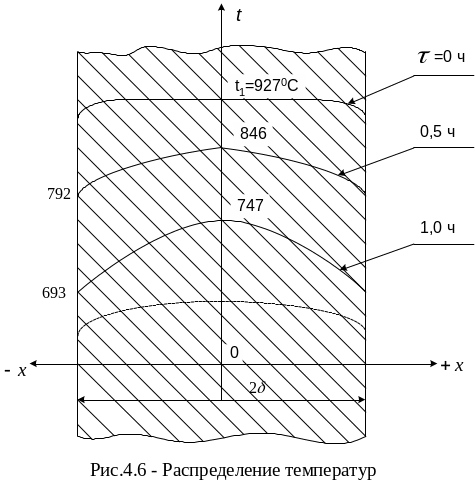
Данная задача может быть решена с использованием графиков (номограмм). На рис. 4.4, 4.5, 4.6 представлены номограммы для определения температуры в телах (пластине, цилиндре, шаре).

Недостатком номограмм, как и таблиц, является то, что они пригодны только для определения температуры в центре тела и на его поверхности.

Рассмотрим задачу, взятую с исходными данными из примера 4.2.

1. При известных значениях критериев Bi=0,2 и F₀=0,4 (для τ=0,5 ч) из номограмм (рис. 4.4, 4.5) получается 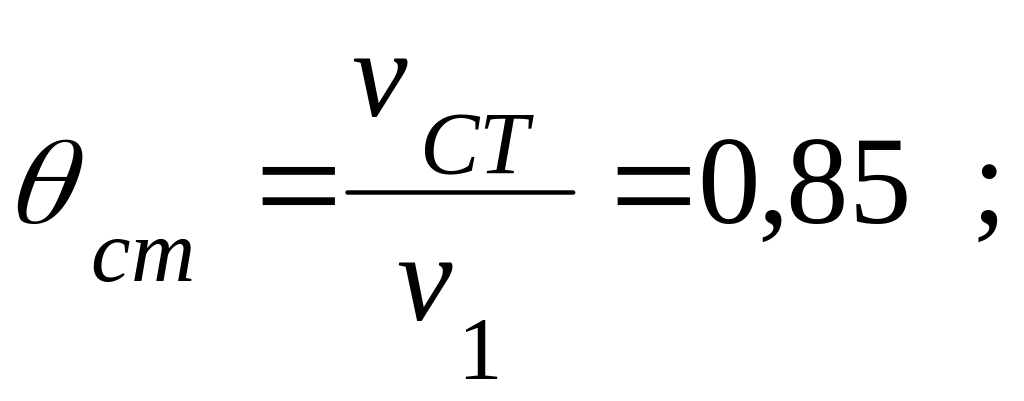и .

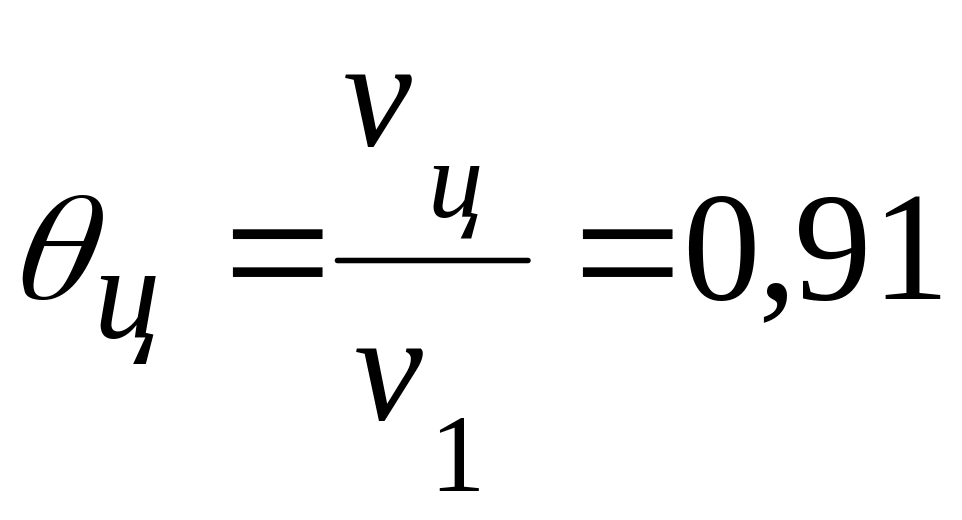2. Используя формулу 4.35, получим:

а) температуру на поверхности цилиндра

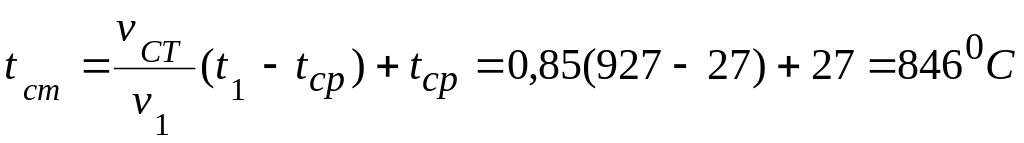
б) температура в центре цилиндра

.

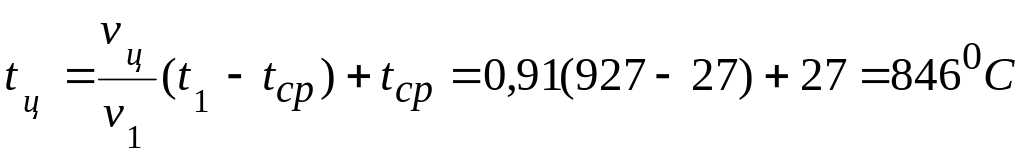3. При известных значениях критериев

Bi=0,2 и F₀=0,8 (τ=1,0 ч) из номограмм (рис. 4.4, 4.5) получаем

.

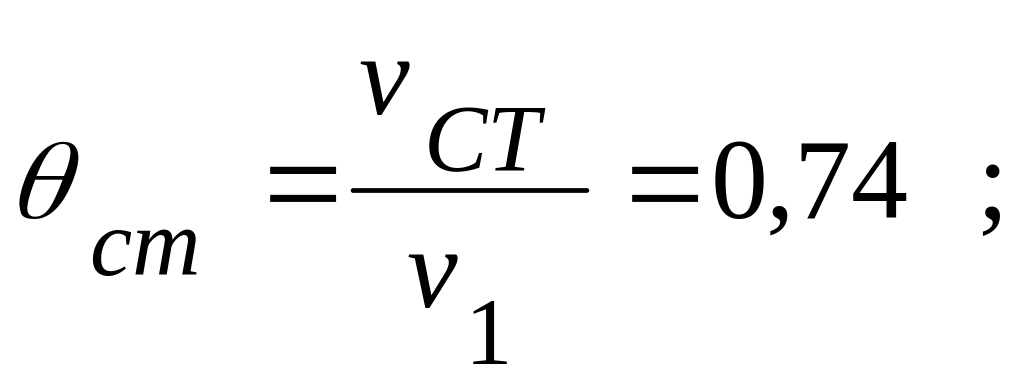
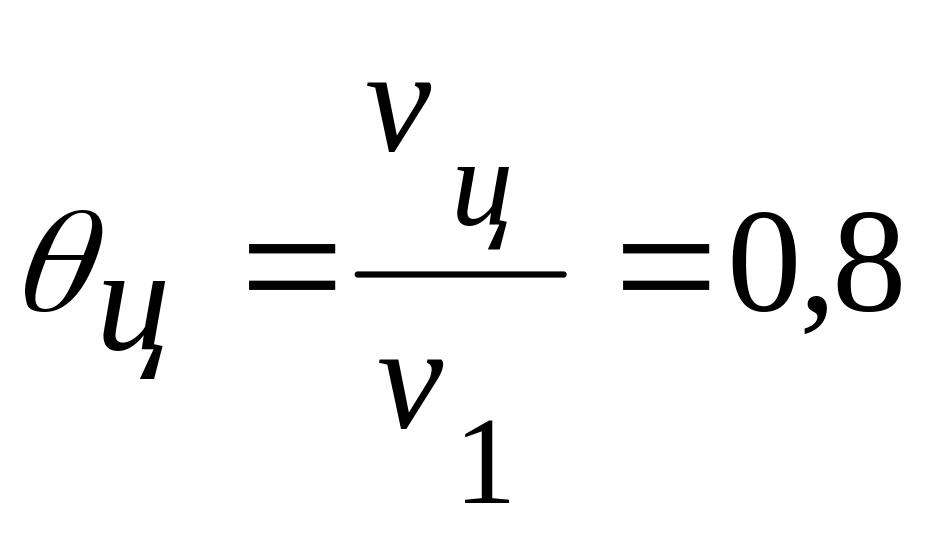Следовательно,

;

Таким образом, с увеличением времени охлаждения температуры поверхности и центра цилиндра уменьшаются.

Для решения аналогичной задачи при отсутствии таблиц и монограмм используется характеристическое уравнение вида [7]

(4.37)

или по формулам, приведённым к таблице.

(при B_i<0,1; F₀≥0,3)

где

t – температура пластины на расстоянии к от средней плоскости в момент времени τ; считая от начала охлаждения (нагревания)

t₀ – начальная температура тела;

t_ж – постоянная температура жидкости (газа).

4.3 Конвективный теплообмен

4.3.1 Основные понятия теории конвективного теплообмена

Понятие конвективного теплообмена охватывает процесс теплообмена при движении жидкости или газа. При этом процесс переноса тепла осуществляется одновременно конвекцией и теплопроводностью.

Эксперименты и теоретические исследования показали, что конвективный теплообмен определяется многими факторами. Главными из них являются:

- характер и режим движения (вынужденное или свободное движение, ламинарный или турбулентный режим);

- скорость движения теплоносителя;

- физические свойства и состояние теплоносителя (газа или жидкости, передающих тепло стенкам сосудов или трубопроводов);

- форма, состояние и размеры поверхности твердого тела (стенки сосудов, труб);

- направление и величина теплового потока.

Решение задачи конвективного теплообмена сводится к определению теплового потока, идущего от теплоносителя в стенку и обратно.

При движении теплоносителя на поверхности стенки возникает пограничный слой, состоящий из двух частей:

а) турбулентной части пограничного слоя – переходной зоны от турбулентного течения к ламинарному;

б) ламинарного слоя (ламинарного подслоя).

В турбулентной части основное количество тепла переносится за счет тепловой конвекции, путем интенсификации перемешивания частиц.

В ламинарной части перенос тепла в направлении нормали к стенке осуществляется в основном теплопроводностью.

Согласно закону сохранения энергии, количество теплоты, отдаваемой единицей поверхности тела окружающей среде в единицу времени вследствие теплоотдачи, должно быть равно теплоте, которая путем теплопроводности подводится к единице поверхности в единицу времени со стороны внутренних частей тела, т.е.

(4.23)

или - дифференциальное уравнение теплоотдачи.

Для определения теплового потока q необходимо знать температурный градиент _ст, что очень трудно осуществить.

Количество тепла, передаваемого стенке путем конвекции, определяется по формуле Ньютона – Рихмана

, (4.24)

где - толщина пограничного слоя;

- средняя температура в ядре потока газа (жидкости);

- средняя температура у стенки.

Обозначив - коэффициент теплоотдачи, формулу (4.24) можно выразить в виде

(4.25)

В инженерной практике часто используют уравнение Ньютона-Рихмана в виде

, (4.26)

где - площадь поверхности теплообмена, ;

- время, с.

Сложность расчета заключается в определении коэффициента . Коэффициент определяет интенсивность теплообмена между поверхностью стенки и окружающей средой и численно равен удельному тепловому потоку при температурном напоре, равном 1С.

Коэффициент зависит от многих факторов, но при решении задач теплоотдачи его в большинстве случаев принимают величиной постоянной.

Для определения коэффициента используют теоретико-экспериментальный путь (метод).