1) . Тогда интеграл вычисляется так:

поскольку при имеем и

2) . Тогда

то есть интеграл расходится, поскольку при .

3) . Тогда

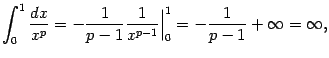
и интеграл снова расходится, поскольку при , если показатель .

Заметим также, что при интеграл не является несобственным: это обычный (то есть собственный) интеграл от непрерывной ограниченной функции. Единственная неприятность получается при , поскольку тогда подынтегральная функция не определена при (и тождественно равна 1 при ). Но мы знаем, согласно одному из свойств определённого интеграла, что значение подынтегральной функции в одной точке можно изменить без изменения значения интеграла. Так что достаточно переопределить значение в 0, положив и получив собственный интеграл

Пример 4.10   Как частные случаи предыдущего примера, получаем, что

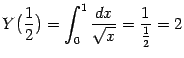
(интеграл сходится), а

(интеграл расходится).

Пример 4.11   Согласно замечанию 4.5, из примера 4.9 следует, что интеграл

(с особенностью функции в правом конце) сходится при и расходится при .

Билет 15: Сравнение бесконечно малых величин.

Сравнение бесконечно малых величин

Зададимся вопросом, как можно сравнить две бесконечно малые величины или две бесконечно большие величины?

Определения. Пусть при функции f(x) и g(x) являются бесконечно малыми. Тогда:

2. Если , то f(x) называется бесконечно малой высшего порядка относительно g(x).

2. Если (конечен и отличен от 0), то f(x) называется бесконечно малой n-го порядка относительно g(x).

3. Если , то f(x) и g(x) называются эквивалентными бесконечно малыми. Эквивалентность записывается так: .

Свойства эквивалентных бесконечно малых:

1. Разность двух эквивалентных бесконечно малых есть бесконечно малая высшего порядка относительно каждой из них.

2. Если из суммы нескольких бесконечно малых разных порядков отбросить бесконечно малые высших порядков, то оставшаяся часть, называемая главной, эквивалентна всей сумме.

Из первого свойства следует, что эквивалентные бесконечно малые могут сделаться приближенно равными со сколь угодно малой относительной погрешностью. Поэтому знак мы применяем как для обозначения эквивалентности бесконечно малых, так и для записи приближенного равенства их достаточно малых значений.

Билет 16: Непрерывность и точки разрыва функции (http://edu.Dvgups.Ru/metdoc/enf/vmatem/semestr1/1-13.Htm - куча примеров http://www.Math24.Ru/continuity-of-functions.Html - непрерывность)

Дадим теперь определение точек разрыва функции.

        Определение 3.2   Точка называется точкой разрыва функции , если она определена в некоторой проколотой окрестности точки (то есть определена на некотором интервале, для которого служит внутренней точкой, но в самой точке , возможно, не определена) и выполняется хотя бы одно из следующих условий:

1) не существует предела слева ;

2) не существует предела справа ;

3) пределы слева и справа существуют, но не равны друг другу: ;

4) пределы слева и справа существуют и равны друг другу: , но не совпадают со значением функции в точке : , или функция не определена в точке .

Если имеет место либо случай 3, либо случай 4, то точка разрыва называется точкой разрыва первого рода, а поведение функции в окрестности точки называется разрывом первого рода в точке ; в случае 4 точка разрыва первого рода называется устранимой точкой разрыва, а разрыв функции в этой точке -- устранимым разрывом.

Если же имеет место либо случай 1, либо случай 2 (либо и тот и другой сразу), то точка разрыва называется точкой разрыва второго рода, а поведение функции в окрестности этой точки -- разрывом второго рода в точке .     

Итак, если функция имеет разрыв первого рода в точке , то существуют, как часто говорят, значения функции "на берегах разрыва": и , но точка не является точкой непрерывности.

Рис.3.2.  -- точка разрыва первого рода

Если значения на берегах разрыва разные, то значение функции в точке может быть любым (или вообще отсутствовать), всё равно будет давать разрыв первого рода. Если же значения на берегах разрыва совпадают, то для наличия разрыва нужно, чтобы либо эти совпадающие значения были отличны от значения функции в точке , либо функция в этой точке была вовсе не определена. Если в этом случае переопределить (или доопределить) функцию в точке , положив , то полученная изменённая функция будет уже непрерывна в точке и разрыв в точке исчезнет; отсюда и название такого разрыва -- устранимый.

Рис.3.3.  -- точка устранимого разрыва

Наконец, к разрывам второго рода, как видно из определения, относятся все разрывы, которые не принадлежат к разрывам первого рода; некоторые из возможных способов поведения функции в окрестности точки , где происходит разрыв второго рода, представлены на следующем рисунке.

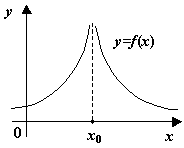
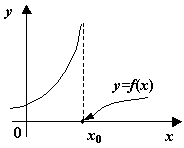
Рис.3.4.  -- точка разрыва второго рода. Некоторые возможные варианты

        Пример 3.3   Рассмотрим функцию 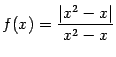, для которой

Функция имеет разрывы при и при . Нетрудно видеть, что при В точках и функция имеет неустранимые разрывы первого рода. В точке имеем:

(значения на краях разыва существуют, но не совпадают); в точке  --

(снова пределы слева и справа существуют, но не совпадают).     

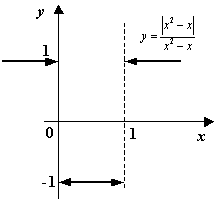
Рис.3.5.График функции

        Пример 3.4   Функция имеет при разрыв второго рода, так как при и при .     

Рис.3.6.График функции

Непрерывная функция — функция без «скачков», то есть такая, у которой малые изменения аргумента приводят к малым изменениям значения функции.

Непрерывная функция, вообще говоря, синоним понятия непрерывное отображение, тем не менее чаще всего этот термин используется в более узком смысле — для отображений между числовыми пространствами, например, на вещественной прямой. Эта статья посвящена именно непрерывным функциям, определённым на подмножестве вещественных чисел и принимающим вещественные значения.