Билет 14: Несобственный интеграл второго рода. (http://webmath.Exponenta.Ru/s/kiselev2/node27.Htm )

Пусть на полуинтервале задана функция , интегрируемая на любом отрезке , где , однако не интегрируемая на отрезке . В точке эта функция может быть вовсе не определена и стремиться к при , любо вовсе не иметь никакого предела при этой базе. Рассмотрим функцию

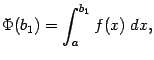
она определена при . Эта функция может иметь предел при (левосторонний предел). Этот предел мы будем называть значением интеграла от по всему полуинтервалу и обозначать в точности как обычный интеграл:

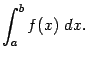
Итак, дадим такое определение:

Определение 4.6   Пусть функция удовлетворяет указанным выше условиям на . Несобственным интегралом второго рода назовём тогда интеграл

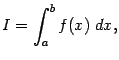
значение которого равняется левостороннему пределу

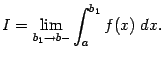
Если этот предел существует, то несобственный интеграл называется сходящимся, а если предела не существует, то расходящимся. Расходящемуся интегралу не приписывается никакого числового значения; в этом случае будем условно писать

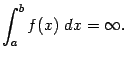
Геометрически вычисление несобственного интеграла второго рода представляет собою (при ) исчерпание плошади неограниченной фигуры под графиком функции над с помощью вычисления плошадей ограниченных фигур, получающихся над отрезком , а затем приближением правого конца к точке (см. рис.).

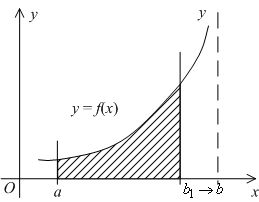
Рис.4.7.

Итак, площадь неограниченной фигуры, изображённой на рисунке, по определению равна значению несобственного интеграла .

Пример 4.8   Найдём площадь фигуры, расположенной под графиком функции над промежутком . (Заметим, что функция не определена при и стремится к при , так что указанная фигура -- неограниченная и площадь задаётся несобственным интегралом второго рода (см. рис.):

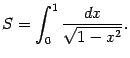
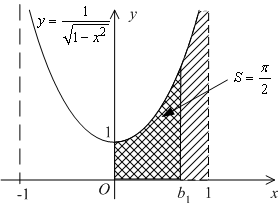
Рис.4.8.

Возьмём и вычислим обычный (собственный) определённый интеграл

Имеем по теореме Ньютона - Лейбница:

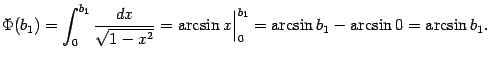
Далее вычисляем предел:

Поскольку оказалось, что предел существует, то несобственный интеграл сходится, а искомая площадь равна его значению:

Замечание 4.4   Как и в случае несобственных интегралов первого рода, часто понимают вычисление предела подстановки 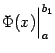как подстановку с верхним предельным значением :

имея в виду, что подстановка верхнего предела интегрирования означает переход к левостороннему пределу при .

При таком обозначении запись вычисления в предыдущем при=мере выглядит так:

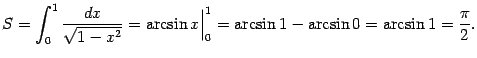
Заметим, что здесь мы, глядя на эти вычисления, могли и не заметить, что вычисляемый интеграл -- несобственный. Это произошло потому, что первообразная , которую мы использовали для вычисления подстановки, непрерывна слева в точке .

Определение 4.7   Аналогично интегралу по полуинтервалу от функции с особенностью в точке , определяется несобственный интеграл второго рода от функции , имеющей особенность в точке полуинтервала :

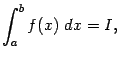
если существует предел

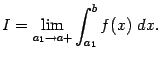
В случае существования указанного предела интеграл называется сходящимся, а в случае, когда предел не существует, -- расходящимся.

Замечание 4.5   Если сделать замену , то несобственный интеграл от функции, имеющей особенность в правом конце промежутка интегрирования, переходит в несобственный интеграл от функции с особенностью в левом конце промежутка, и наоборот (проверьте это утверждение, сделав замену в интеграле , где при ). Поэтому свойства несобственных интегралов второго рода достаточно устанавливать лишь в каком-нибудь одном случае, например, в случае особенности в правом конце промежутка, а свойства интегралов с особенностью функции в левом конце будут получаться очевидными переформулировками.

Пример 4.9   Рассмотрим интеграл

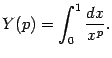
Если , то подынтегральная функция стремится к при , так что получается несобственный интеграл второго рода.

Рассмотрим такие случаи: