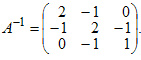Билет 4:Векторное произведение двух векторов и его основные свойства.

Определение. Векторным произведением двух векторов и называется новый вектор , модуль которого равен площади параллелограмма, построенного на векторах и , приведенных к общему началу, и который перпендикулярен к перемножаемым векторам (иначе говоря, перпендикулярен к плоскости построенного на них параллелограмма) и направлен в такую сторону, чтобы кратчайший поворот от к вокруг полученного вектора представлялся происходящим против часовой стрелки, если смотреть из конца вектора (рис. 40).

Если векторы и коллинеарны, то их векторное произведение считается равным нулевому вектору. Из этого определения следует, что

| | = | | | | sin ,

где - угол между векторами и (0 ). Векторное произведение векторов и обозначается символом

х или [ ] или [ , ].

Выясним физический смысл векторного произведения. Если вектор изображает приложенную в некоторой точке М силу, а вектор идет из некоторой точки О в точку М, то вектор =[ ] представляет собой момент силы относительно точки О.

Свойства векторного произведения

1 . При перестановке сомножителей векторное произведение меняет знак, т.е.

х = -( x ).

2.

( )х = х( )= ( х ), где - скаляр.

3. Векторное произведение подчиняется распределительному закону, т.е.

( + ) x = x + x .

4. Если векторное произведение двух векторов равно нулевому вектору, то либо равен нулевому вектору хотя бы один из перемножаемых векторов (тривиальный случай), либо равен нулю синус угла между ними, т.е. векторы коллинеарны.

Обратно, если два ненулевых вектора коллинеарны, то их векторное произведение равно нулевому вектору.

Таким образом, для того чтобы два ненулевых вектора и были коллинеарны, необходимо и достаточно, чтобы их векторное произведение равнялось нулевому вектору.

Отсюда, в частности, следует, что векторное произведение вектора на самого себя равно нулевому вектору:

х =0

( х еще называют векторным квадратом вектора .

Билет 5: Смешанное произведение трех векторов. Свойства смешанного произведения. Условие компланарности трех векторов.

Определение смешанного произведения.

Смешанное произведение определяется для трех векторов, заданных в трехмерном пространстве.

Определение.

Смешанным произведением трех векторов и называется действительное число, равное скалярному произведению векторов и , где - векторное произведение векторов и .

Из определения понятно, почему смешанное произведение часто называют векторно-скалярным произведением.

Смешанное произведение векторов и обычно обозначают . В таких обозначениях по определению смешанного произведения .

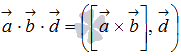Смешанное произведение в координатной форме.

Покажем, как находится смешанное произведение, если известны координаты умножаемых векторов в прямоугольной системе координат. Пусть - координатные векторы.

Векторное произведение в координатах имеет вид а скалярное произведение векторов в прямоугольной системе координат равно сумме произведений соответствующих координат, поэтому,

Таким образом, смешанное произведение векторов равно определителю матрицы третьего порядка, строками которой являются координаты умножаемых векторов, то есть, .

Свойства смешанного произведения.

Из свойств векторного произведения и свойств скалярного произведения следуют следующие свойства смешанного произведения:

;

;

Очевидно, что если хотя бы один из умножаемых векторов нулевой, то смешанное произведение равно нулю.

Смешанное произведение также равно нулю, если хотя бы два умножаемых вектора равны.

Действительно, если , то по определению векторного произведения 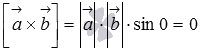, следовательно, смешанное произведение равно нулю, так как 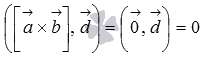. Если же или , то угол между векторами и равен , следовательно, по определению скалярного произведения векторов .

Свойства смешанного произведения обычно применяются при доказательстве тождеств или неравенств.

Рассмотрим несколько характерных задач.

Пример.

Докажите равенство 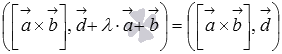, где - некоторое действительное число.

Решение.

Преобразуем левую часть равенства, обратившись к третьему свойству смешанного произведения:

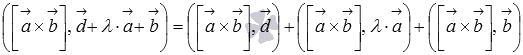
Выше мы показали, что 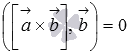, следовательно,

По первому свойству смешанного произведения , а . Таким образом, .

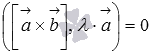Поэтому,

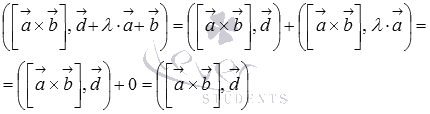
Что и требовалось доказать.

Пример.

Докажите, что модуль смешанного произведения трех векторов не превосходит произведения длин этих векторов.

Решение.

Иными словами, нам требуется доказать неравенство .

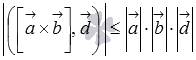По определению скалярного и векторного произведения векторов, мы можем записать

Из свойств основных элементарных функций мы знаем, что 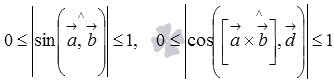. Следовательно, 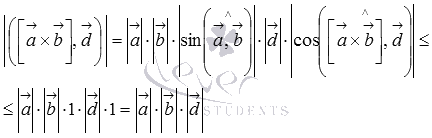что и требовалось доказать.

Вычисление смешанного произведения, примеры и решения.

Проще всего смешанное произведение находится, когда известны координаты векторов. Для вычисления используется формула .

Пример.

Даны координаты трех векторов в прямоугольной системе координат . Найдите смешанное произведение .

Решение.

Мы выяснили, что смешанное произведение векторов может быть вычислено через определитель матрицы третьего порядка, строками которой являются координаты векторов, то есть,

Ответ:

.

Пример.

Найдите векторно-скалярное произведение векторов , где - орты прямоугольной декартовой системы координат.

Решение.

Данные векторы имеют следующие координаты (при необходимости смотрите статью координаты вектора в прямоугольной системе координат)

Осталось воспользоваться формулой для вычисления смешанного произведения через координаты векторов

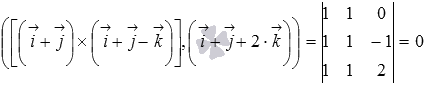
Ответ:

.

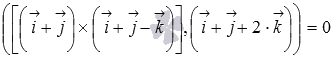Смешанное произведение векторов также может быть вычислено, если известны длины векторов и углы между ними. Рассмотрим решение характерного примера.

Пример.

В правой прямоугольной декартовой системе координат заданы три взаимно перпендикулярных вектора и , образующих правую тройку, их длины равны соответственно 4, 2 и 3. Найдите их смешанное произведение .

Решение.

Обозначим .

Нам известно, что скалярное произведение векторов равно произведению их длин на косинус угла между ними, поэтому .

Сразу подставим значение длины вектора , известное из условия: .

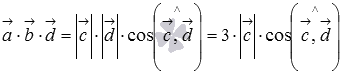У нас остались неизвестные и . Найдем их.

По условию , тогда по определению векторного произведения находим длину вектора :

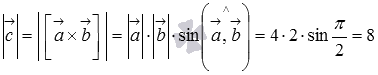
Из определения векторного произведения мы можем заключить, что вектор перпендикулярен вектору и вектору , причем тройка векторов будет правой, так как векторы и заданы в правой прямоугольной декартовой системе координат. Следовательно, векторы и будут сонаправленными, то есть, .

Подставляем полученные результаты и получаем искомое смешанное произведение: .

Ответ:

.

Билет 6: Общее уравнение плоскости. Угол между двумя плоскостями. (http://edu.dvgups.ru/METDOC/ENF/VMATEM/WM/METOD/SYASINA/WEBUMK/frame/2_3.htm , так же сайт http://tvsh2004.narod.ru/dk_pr.html http://www.toehelp.ru/theory/math/lecture19/lecture19.html )

Общее уравнение плоскости

После преобразования, уравнение

 

можно записать в виде , приняв , получаем общее уравнение плоскости . Уравнение плоскости в отрезках Если же общее уравнение плоскости является полным     (т.е. ни один из коэффициентов не равен нулю), то его можно преобразовать к виду, называемому уравнением плоскости в отрезках ,    равны величинам отрез­­ков, отсекаемых плоскостью на координатных осях.

 

Уравнение плоскости, проходящей через три данные точки

Пусть плоскость проходит через точки  и , не лежащие на одной прямой и  – произвольная точка плоскости. Тогда векторы ,

  ,  компланарны. Следовательно, их смешанное произведение равно нулю. Используя координатную запись смешанного произведения, получаем:

.

 

Это уравнение, которому удовлетворяют координаты  любой точки, лежащей на искомой плоскости, является уравнением плоскости, проходящей через три данные точки.

УГОЛ МЕЖДУ ПЛОСКОСТЯМИ

Р ассмотрим две плоскости α₁ и α₂, заданные соответственно уравнениями:

Под углом между двумя плоскостями будем понимать один из двугранных углов, образованных этими плоскостями. Очевидно, что угол между нормальными векторами и плоскостей α₁ и α₂ равен одному из указанных смежных двугранных углов или . Поэтому . Т.к. и , то

.

Пример. Определить угол между плоскостями x+2y-3z+4=0 и 2x+3y+z+8=0.

Условие параллельности двух плоскостей.

Две плоскости α₁ и α₂ параллельны тогда и только тогда, когда их нормальные векторы и параллельны, а значит .

Итак, две плоскости параллельны друг другу тогда и только тогда, когда коэффициенты при соответствующих координатах пропорциональны:

или

Условие перпендикулярности плоскостей.

Ясно, что две плоскости перпендикулярны тогда и только тогда, когда их нормальные векторы перпендикулярны, а следовательно, или .

Таким образом, .

Примеры.

Составить уравнение плоскости, проходящей через точку

M(-2; 1; 4) параллельно плоскости 3x+2y-7z+8=0.

Уравнение плоскости будем искать в виде Ax+By+Cz+D=0. Из условия параллельности плоскостей следует, что: . Поэтому можно положить A=3, B=2, C=-7. Поэтому уравнение плоскости принимает вид3x+2y-7z+D=0.

Кроме того, так какM α, то-6+2-28+D=0, D=32.

Итак, искомое уравнение 3x+2y-7z+32=0.

Составить уравнение плоскости, проходящей через точки M₁(1; 1; 1), M₂(0; 1; –1) перпендикулярно плоскости x+y+z=0.

Так как M₁ α, то используя уравнение плоскости, проходящей через заданную точку, будем иметь A(x-1)+B(y-1)+C(z-1)=0.

Далее, так как M₂ α, то подставив координаты точки в выписанное уравнение, получим равенство -A-2C=0 или A+2C=0.

Учтем, что заданная плоскость перпендикулярна искомой. Поэтому A+B+C=0.

Выразим коэффициенты Aи Bчерез C: A=-2C, B=C и подставим их в исходное уравнение: -2C(x-1)+C(y-1)+C(z-1)=0.

Окончательно получаем -2x+y+z=0.

Составить уравнение плоскости, проходящей через точку M(-2; 3; 6) перпендикулярно плоскостям 2x+3y-2z-4=0 и 3x+5y+z=0.

Так как M α, то A(x+2)+B(x-3)+C(z-6)=0.

По условию задачи , поэтому

Итак уравнение плоскости принимает вид 13(x+2)-8(y-3)+z-6=0 или 13x-8y+z+44=0.

Билет 7: Матрицы. Обратная матрица (https://ru.wikipedia.org/wiki/%D0%9E%D0%B1%D1%80%D0%B0%D1%82%D0%BD%D0%B0%D1%8F_%D0%BC%D0%B0%D1%82%D1%80%D0%B8%D1%86%D0%B0 )

http://www.grandars.ru/student/vysshaya-matematika/obratnaya-matrica.html -- обратные матрицы

Матрицей называется прямоугольная таблица чисел, состоящая из m одинаковой длины строк или n одинаковой длины стробцов.

aij- элемент матрицы, который находится в i-ой строке и j-м столбце.

Вид матрицы:

квадратная

Квадратная матрица - это матрица с равным числом столбцов и строк.

Обра́тная ма́трица — такая матрица A⁻¹, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E:

Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует. Однако возможно обобщить это понятие и ввести псевдообратные матрицы, похожие на обратные по многим свойствам.

Пусть имеется квадратная матрица n-го порядка

Матрица А^-1 называется обратной матрицей по отношению к матрице А, если А*А^-1 = Е, где Е — единичная матрица n-го порядка.

Единичная матрица — такая квадратная матрица, у которой все элементы по главной диагонали, проходящей от левого верхнего угла к правому нижнему углу, — единицы, а остальные — нули, например:

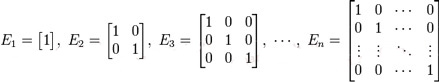
Обратная матрица может существовать только для квадратных матриц т.е. для тех матриц, у которых число строк и столбцов совпадают.

Пример!

Алгоритм нахождения обратной матрицы

Записать в таблицу для решения систем уравнений методом Гаусса матрицу А и справа (на место правых частей уравнений) приписать к ней матрицу Е.

Используя преобразования Жордана, привести матрицу А к матрице, состоящей из единичных столбцов; при этом необходимо одновременно преобразовать матрицу Е.

Если необходимо, то переставить строки (уравнения) последней таблицы так, чтобы под матрицей А исходной таблицы получилась единичная матрица Е.

Записать обратную матрицу А^-1, которая находится в последней таблице под матрицей Е исходной таблицы.

Пример 1

Для матрицы А найти обратную матрицу А^-1

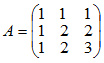
Решение: Записываем матрицу А и справа приписываем единичную матрицу Е. Используя преобразования Жордана, приводим матрицу А к единичной матрице Е. Вычисления приведены в таблице 31.1.

Проверим правильность вычислений умножением исходной матрицы А и обратной матрицы А^-1.

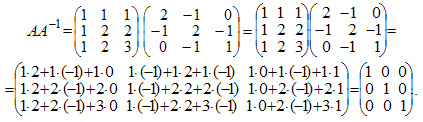
В результате умножения матриц получилась единичная матрица. Следовательно, вычисления произведены правильно.

Ответ: