Билет 32: Гипербола. Свойства гиперболы.
Определение. Гиперболой называется множество точек плоскости, для которых модуль разности расстояний от двух данных точек, называемых фокусами есть величина постоянная, меньшая расстояния между фокусами.
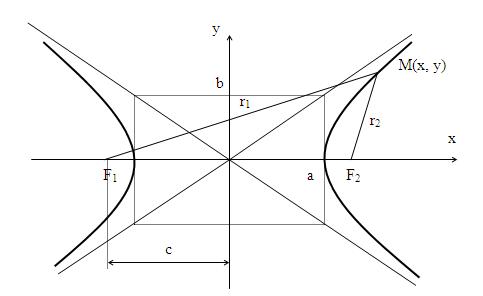
По определению | r 1 – r 2 | = 2 a . F 1 , F 2 – фокусы гиперболы. F 1 F 2 = 2 c .
Выберем на гиперболе произвольную точку М(х, у). Тогда :
обозначим с2 – а2 = b2 (геометрически эта величина – меньшая полуось)
Получили каноническое уравнение гиперболы.Гипербола симметрична относительно середины отрезка, соединяющего фокусы и относительно осей координат.
Ось 2а называется действительной осью.
Ось 2 b называется мнимой осью.
Гипербола
имеет две асимптоты, уравнения которых
Свойства гиперболы.
Теорема. (Свойства гиперболы.)
1. В канонической для гиперболы системе координат, в полосе
нет точек гиперболы.
2.
Точки
лежат
на гиперболе.
3. Гипербола является кривой, симметричной относительно своих главных осей.
4. Центр гиперболы является его центром симметрии.
Доказательство. 1, 2) Сразу же следует из канонического уравнения гиперболы.
3, 4) Пусть М(х, у) – произвольная точка гиперболы. Тогда ее координаты удовлетворяют уравнению (4). Но тогда координаты точек также удовлетворяют уравнению (4), и, следовательно, являются точками гиперболы, откуда и следуют утверждения теоремы.
Теорема доказана.
Билет 33: Парабола. Свойства параболы
Пара́бола (греч. παραβολή — приложение) — геометрическое место точек, равноудалённых от данной прямой (называемой директрисой параболы) и данной точки (называемой фокусом параболы).
Наряду с эллипсом и гиперболой, парабола является коническим сечением. Она может быть определена как коническое сечение с единичным эксцентриситетом.
Свойства:
Свойства параболы. |
|
1) парабола – кривая второго порядка 2)
Парабола симметрична относительно
оси
3)
4)
Разрешим уравнение относительно
функция выпукла вверх.
5) Оптическое свойство: оптические лучи, исходящие из фокуса параболы, отразившись от нее идут параллельно ее оси. |
.
Ось симметрии параболы называют ее
осью
-
вершина параболы
.
в
первой четверти
,
.
Парабола расположена в полуплоскости
справа от
.
Если
возрастает
от 0 до
,
то
тоже
возрастает от 0 до
.
Парабола - линия неограниченная.
Билет 34: Формула Тейлора с остаточным членом в форме Пеано или Лагранжа
Остаточный член формулы Тейлора.
Пусть
.
Тогда в некоторой окрестности
можно
написать равенство
,
которое
называется формулой Тейлора функции
в
точке
,
где
называется
многочленом Тейлора, а
-
остаточным членом Тейлора (после
n-го члена).
Если существует
,
то согласно
определению сходимости ряда (1) сходится
к функции
в
точке
.
Лемма
Пусть
в
.
Тогда в
Доказательство:
Теорема.
Формула с остаточным членом в форме
Лагранжа. Пусть
,
непрерывна
на отрезке
,
на
интервале
.
Тогда справедлива формула (1), в которой
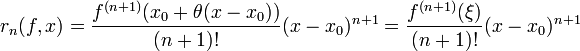
где
.
Доказательство:
будем проводить по индукции, считая
.
При
теорема
утверждает, что при некотором
Это утверждение верно, так как оно совпадает с доказанной ранее формулой конечных приращений Лагранжа.
Предположим,
что утверждение верно при
и
установим, что оно верно и при n. Использую
теорему Коши о среднем и лемму, имеем
(для определенности
)
где
,а
предпоследнее равенство написано в
силу предположения индукции.
Теорема доказана.
Теорема. Формула Тейлора с остаточным членом в форме Пеано.
Пусть
и
.
Тогда справедлива формула (1), в которой
при
.
Доказательство: будем проводить по индукции:
При
утверждение
теоремы верно. В самом деле, в этом случае
дифференцируема
в точке
.
Следовательно,
Что совпадает с условием теоремы.
Предположим,
что утверждение теоремы верно при
и
покажем, что это верно и для n.
Использую теорему Лагранжа о конечных приращениях и лемму, имеем (считая для определенности ):
где
.
По предположению
индукции
при
.
Следовательно,
при .
что и требовалось показать.