В файле про предел. Билет 22: Касательная и нормаль к плоской кривой. Угол между двумя кривыми

Касательной к кривой линии называется прямая, представляющая предельное положение секущей.

На рисунках 85 и 86 представлены алгоритмы построения касательной к плоской кривой линии соответственно параллельно направлению и из точки, не принадлежащей кривой.

Рисунок 85. Касательная к кривой параллельная заданному направлению		Рисунок 86. Касательная к кривой из заданной точки

Рисунок 87. Касательная в точке кривой

Для построения касательной в точке плоской кривой как видно из рисунка 87 используется две секущие хорды. Рассмотрим построение касательной в точке А. Для этого проведем секущие хорды АЕ и АD. Если точку Е приближать к точке А, секущая АЕ поворачивается вокруг точки А. Когда точка Е совпадет с точкой А (А≡Е) секущая АЕ достигнет своего предельного положения t. В этом предельном положении секущая называется полукасательной к кривой а в точке А. Секущая АD в предельном положении А≡D также представлена полукасательной t.

Кривая линия в точке А имеет две полукасательные прямые, которые совпадают и определяют одну касательную к кривой линии в точке А – кривая в этой точке называется гладкой (плавной).

Кривая плавная во всех её точках называется гладкой (плавной) кривой линией.

На кривой линии могут быть точки, в которых разнонаправленные полукасательные не принадлежат одной прямой, а составляют между собой угол. Так на кривой а в точке В угол δ между полукасательными не равен 180⁰. Точка В в этом случае называется точкой излома или выходящей точкой.

Нормалью п в точке А кривой линии называется перпендикуляр к касательной (рис.87).

Построение нормали к кривой проходящей через точку А, не принадлежащую кривой m, можно выполнить следующим образом (рис.88):

Рисунок 88. Построение нормали к кривой

1. Проведем окружности а₁, а₂, а₃, а₄, разных радиусов с центром в точке А;

2. Отметим точки пересечения окружностей с кривой -1, 1₁, 2, 2₁, 3, 3₁, 4, 4₁;

3. Из концов хорд восстановим перпендикуляры (при этом перпендикуляры, восстановленные из точек 1, 2, 3, 4, имеют противоположное направление перпендикулярам, восстановленным из точек 1₁, 2₁, 3₁, 4₁);

4. На полученных перпендикулярах отложим отрезки, равные длине соответствующих хорд;

5. Полученные точки соединим плавной кривой l;

6. Пересечение кривых m и l определит положение точки К, через которую пройдет искомая нормаль n.

 Второй вопрос по билету:

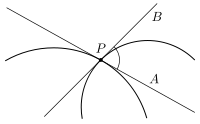
Угол между двумя кривыми в точке Р определяется как угол между касательными А и В в P

Билет 23: Направление выпуклости кривой и точки перегиба. (http://glaznev.Sibcity.Ru/1kurs/der/html/lek_d8.Htm )

Выпуклость и вогнутость кривой. Точки перегиба

 

Определение 4

Мы говорим, что кривая обращена выпуклостью вверх на интервале

(a, b), если все точки кривой лежат ниже любой ее касательной на этом интервале.

Мы говорим, что кривая обращена выпуклостью вниз на интервале

(b, c), если все точки кривой лежат выше любой ее касательной на этом интервале.

Кривую, обращенную выпуклостью вверх, будем называть выпуклой, а обращенную выпуклостью вниз – вогнутой.

Направление выпуклости кривой является важной характеристикой ее формы. Докажем следующую теорему.

 

Теорема 6

Если во всех точках интервала (а, b) вторая производная функции f(x) отрицательна, т.е. f"(x) <0, то кривая y=f (x) на этом интервале обращена выпуклостью вверх (кривая выпуклая).

 

Теорема 6'

Если во всех точках интервала (b, c) вторая производная функции f(x) положительна, т.е. f"(x) >0, то кривая y=f (x) на этом интервале обращена выпуклостью вниз (кривая вогнутая).

 

Определение 5

Точка, отделяющая выпуклую часть непрерывной кривой от вогнутой, называется точкой перегиба кривой.

Очевидно, что в точке перегиба касательная, если она существует, пересекает кривую, так как с одной стороны от этой точки кривая лежит под касательной, а с другой стороны – над нею.

 

 

 

 

 

Теорема 7

Пусть кривая определяется уравнением y=f (x). Если f"(а) = 0 или f"(а) не существует и при переходе через значение x=a производная f"(x) меняет знак, то точка кривой с абсциссой x=a есть точка перегиба.

 

Алгоритм исследования на выпуклость и точки перегиба.

1. Находим область определения функции f (x).

2. Находим производную f″(x) и критические точки 2-го рода.

3. Разбиваем область определения f(x) критическими точками 2-го рода на интервалы.

4. Определяем знак f″(x) в каждом из интервалов, полученных в п. 3.

5. Делаем выводы о направлении выпуклости в каждом интервале и о наличии точек перегиба.

6. Вычисляем координаты точек перегиба.

Пример 4. Найти интервалы выпуклости, вогнутости и точки перегиба графика функции f (x) = (х + 1) ^{1/ 3}.

1. Область определения : (-¥ , +¥).

2. f ‘(x) = 1/3 (х + 1) ^{- 2/ 3}, f″(x) = - 2/9 (х + 1) ^{- 5/ 3}.

f″(x) ¹ 0, f″(x) не существует при х = - 1.

3. (-¥ , -1), ( -1, +¥).

4. f″(x) > 0 при х < - 1, f″(x) < 0 при х > - 1.

5. График функции выпуклый на ( -1, +¥). и вогнутый на (-¥ , -1).

f ( -1) = (-1 + 1) ^{1/ 3} = 0, (-1, 0) - точка перегиба.