6. Слабоструктурированные задачи. Источники неопределенности при принятии решений.
Саймон (1973 г.) слабо структурируемые проблемы ПР – это проблемы, в которых доминируют качественные, плохо определенные факторы, а критерии оценки альтернатив носят как правило субъективный характер, вплоть до того, что набор критериев м.б. определен ЛПР (это может привести к тому, что ЛПР будет тянуть одеяло на себя).
Хорошо структурируемые проблемы ПР – например, математические проблемы, которые можно доказать.
Основные типы неопределенности ПР:
Неопределенность природы (объективная неопределенность – это неопределенность самих изучаемых процессов и явлений). Например, принцип неопределенности Гейзенберга.
Гносеологическая неопределенность – это неопределенность, вызванная отсутствием достаточной инфы.
Стратегическая неопределенность – неопределенность, вызванная зависимостью от других субъектов управления, т.е. противников, партнеров, руководства, соперников.
Неопределенность, вызванная нечеткостью восприятия человеком данных, описывающих исследуемый объект (процесс).
В задачах ПР может присутствовать несколько видов неопределенностей из вышеперечисленных. Неопределенность любого из этих видов в каждых конкретных условиях может иметь свою природу, т.е. проявляться по-разному, => учет неопределенности должен иметь специфические методы.
7. Основные виды неопределенности и способы ее уменьшения
1) Абсолютная неопределенность может иметь место когда неизвестно какое событие произойдет, когда, где и почему. Это нереальная ситуация.
Понятие «абсолютная неопределенность» не соответствует модельным представлениям и далее не будет рассматриваться.
Возьмем
множество
альтернатив,
где
- выходной параметр некоторого объекта,
индекс некоторой ситуации. Г – множество
наших оценок параметра
множества
.
Если мы ничего не знаем о множествах и
,
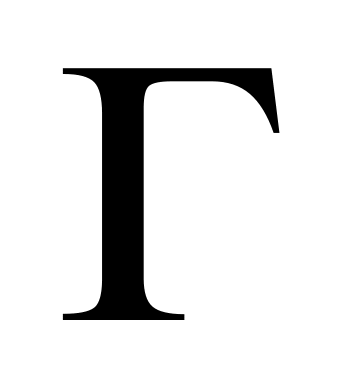то мы имеем дело с полной
неопределенностью.
Для большинства практических ситуаций
такое знание нереалистично.Будем рассматривать только реалистичные ситуации, когда нам известно множество , но не известно как себя ведет параметр на этом множестве. Это случайная неопределенность в широком смысле (стохастическая).
На множестве существует вероятностное распределение и оно нам известно, точно (дан закон распределения) – это байесовская неопределенность.
Нулевая неопределенность (детерминированный метод) тогда это не является неопределенностью.
Борьба с неопределенностью: 1) появление формальной логики, т.е. науки о рассуждениях, которые должны определить неизвестное значение истинности высказывания (Аристотель, 334 г. до н.э. Он открыл основные законы логики).
2) вероятностно-статистические методы. Доминируют статистические методы (характерны для биологов, исторически первый метод).
В настоящее время, на первый план выступает неопределенность, связанная со слабоструктурированными проблемами (задачи не м.б. описаны точно), нечеткость описания объектов является естественной; не оперирует количеством, характерны качественные оценки. Качественные данные несут вполне определенную инфу наряду с количественными.
3) Мягкие вычисления (Л. Заде, 1934г. ) – объединяют нечеткую логику, нейронные сети, генетические алгоритмы, вероятностные рассуждения. Они могут применяться по отдельности, а могут объединяться в гибридные.
Мягкие вычисления = Нечеткие системы + Нейронные сети + Генетические алгоритмы.