40. Обучение нейронных сетей методом статистических испытаний.

Нейронная сеть представляет собой совокупность нейронов, связанных между собой соответствующим образом.

Нейрон – преобразовательный элемент, имеющий некоторое количество входов (синапсов), на которые поступают входные сигналы х_i и один выход (аксон), с которого снимается выходной сигнал у. Каждый синапс имеет вес w_i, на который умножается входной сигнал x_i.

Структура нейрона:

В

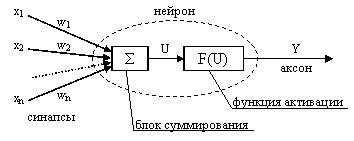
нутри нейрона можно выделить блок суммирования, определяющий взвешенную сумму всех входных сигналов и блок функции активации Y = F(U).

Таким образом, нейрон функционирует за два такта:

1)   суммирование входных сигналов;

2)   вычисление Y по функции активации.

Нейронные сети относятся к классу аппроксиматоров и «черных ящиков», аппроксимирующих некоторые функции вида Y = F(X), где Y – вектор выходных переменных, Х – вектор входных.

Процесс аппроксимации заключается в подборе весовых коэффициентов w_ij и называется обучением НС. То есть НС может функционировать в двух режимах:

1. эксплуатации, когда на вход подаются сигналы, а на выходе снимаются результаты вычислений;

2. обучения, когда происходит корректировка весов таким образом, чтобы выходные сигналы наиболее точно соответствовали желаемым.

От качества обучения НС зависит точность ее работы в режиме эксплуатации.

Структура процесса обучения представлена на рисунке, где обозначены:

 

Y_жел – желаемые значения выходных сигналов,

Е – ошибка обучения (Е = Y_жел – Y),

К – корректирующие воздействия (обычно изменения весов w_ij).

Для обучения НС составляется обучающая выборка входных сигналов и соответствующих им выходных. Выборка может быть разделена на две части: рабочую выборку (на основе которой производится собственно обучение) и тестирующую выборку (для проверки качества обучения).

Далее определяется структура НС.

Существует несколько методов обучения, которые можно классифицировать по способам использования учителя:

1. обучение с учителем (коррекция весов производится исходя из сравнения текущего и желаемого выходных векторов);

2. обучение с последовательным подкреплением знаний (сети не даются желаемые значения выходов, а ставится оценка «хорошо» или «плохо»);

3. обучение без учителя (сеть сама вырабатывает правила обучения путем выделения особенностей из набора входных данных). По использованию элементов случайности методы обучения подразделяются:

- на детерминистские (коррекция на основе анализа входных и выходных сигналов, а также дополнительной информации, например, желаемых выходов);

- на стохастические (случайное изменение весов в ходе обучения – Больцмановское обучение).

Метод статистических испытаний применяется для моделирования сложных систем, в которых не возможно или не целесообразно получить аналитические модели, описывающие протекающие процессы. Данный метод также используется в случаях, когда реальные испытания системы оказываются дорогостоящими или их не возможно проводить по причинам социального, военного и других смыслов. Например, необходимо определить вероятность попадания ракеты в цель. Для этого необходимо произвести 1000 пусков – это дорого. Поэтому строят математический аналог системы, проводят испытания и обрабатывают полученные результаты. Суть метода заключается в замене эксперимента с реальной системой, экспериментом с ее математическим аналогом и имитацией работы системы (имитационное моделирование). Метод статистических испытаний основан на законах больших чисел, а именно на двух предельных теоремах Чебышева и Бернулли.

Теорема Чебышева: при неограниченном проведении опытов среднее арифметическое y по вероятности стремится к математическому ожиданию m_y : 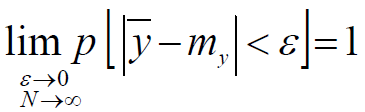где ε > 0.

Теорема Бернулли: при неограниченном увеличении опытов частота

события q сходится по вероятности к его вероятности p: 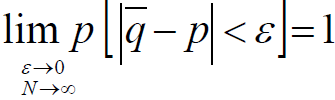где ε > 0.

Теорема Бернулли позволяет определить вероятность совершения некоторого события.

Испытания проводятся следующим образом. Известна некоторая система S (черный ящик). Система S имеет множество входов X (случайные величины) и один выход Y:Ч

тобы построить математический аналог системы, надо разработать алгоритм функционирования системы. Систему представляют как совокупность взаимосвязанных подсистем, на вход которых поступают величины х₁…х_n, распределенные по определенному закону. Эти случайные величины должны пройти определенное количество блоков, чтобы попасть на выход системы. Процесс моделирования заключается в многократном повторении опытов над системой.

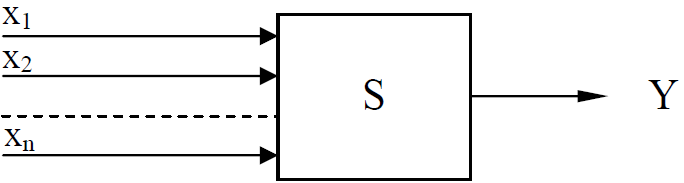
Таким образом, моделирование содержит три этапа:1 Разработка и ввод в ЭВМ моделирующего алгоритма.2 Генерирование входных случайных величин с заданными функциями и параметрами распределения и многократное повторение опытов.3 Статистическая обработка результатов моделирования.