26. Особенности нечеткого логического вывода по Мамдани и Ларсену

Механизм нечеткого логического вывода по Мамдани (Mamdani) - наиболее распространенный способ логического вывода в нечетких системах. В нем используется минимаксная композиция нечетких множеств. Данный механизм включает в себя следующую последовательность действий.

1)Процедура фазификации: определяются степени истинности, т.е. значения функций принадлежности для левых частей каждого правила (предпосылок). Для базы правил с m правилами обозначим степени истинности как A_ik(x_k), i=1..m, k=1..n.

2) Процедура нечеткой импликации: позволяет найти усеченные функции принадлежности (В₁ и В₂) на уровнях (α(х₁) и α(х₂))

3) Композиция, или объединение полученных усеченных функций, для чего используется максимальная композиция, т.е. для каждого значения У находим максимум из усеченных функций В₁ и В₂ :

где (y) – функция принадлежности итогового нечеткого множества. ( На рисунке как MF)

4)Дефазификация, или приведение к четкости. Существует несколько методов дефазификации. Например, центроидный метод.

R₂: Если Х₂ есть А₂, то у есть В₂

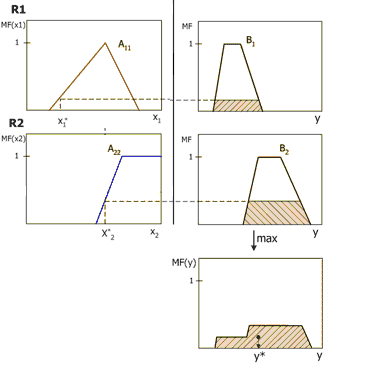Схема нечеткого вывода по Мамдани.

По Ларсену.

П1: если x1 = A1 и x2 = B1 и x3 = C1, то y есть G1,

П2: если x1 = A2 и x2 = B1 и x3 = C1, то y есть G2,

П3: если x1 = A1 и x2 = B2 и x3 = C1, то y есть G3,

………

П10: если x1 = A1 или A2 или A3 и x2 = B3 и x3 = C1 или C2, то y есть G6 и т.д.

где x1, x2, x3 – входные переменные (названия рассматриваемых

характеристик объекта).

y – переменная вывода (название категории для классификации объекта).

A1, A2, A3, B1, B3, C1, C2, C3 и G1, G2, G5, G6 – функции принадлежности,

определённые соответственно на x и y.

28. Нечеткие аппроксиматоры.

При аппроксиматор в простейшем случае представляет собой элемент с несколькими скалярными входами и одним выходом, выполняющий нелинейное параметрическое преобразование суммарного взвешенного входного сигнала в скалярную величину

У=f(Х₁, Х_2,…, Х_m)+ е

f- неизвестная функция.

Над объектом выполняются N испытаний, в итоге получаем N пар значений (х_k,Y_k), где k изменяется от 1 до N, и х_k- вектор.

Затем 1) из общего числа N пар выбираются n<N пар (х_k,Y_k) и из них составляется начальная база знаний в виде матрицы

Х11 Х12 …… Х1m, Y1

…

Хn1 Хn2 …… Хnm, Yn

Каждая строка – одно правило.

2) для каждой экспериментальной точки (х_k,Y_k), рассчитывают прогнозируемое значение по формуле Сугено 1го порядка (//в формуле все х – векторы)

γ( )- многомерная функция Гаусса

|| || - символ эвклидова расстояния.

Получаем колокообразную функцию принадлежности типа функции Гаусса.

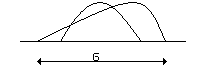σ – размах колокола

3)n- используется в качестве базы правил

d- заданная погрешность аппроксимации

| ŷ- y|>d

При выполнении этого неравенства матрица расширяется за счет дополнительной строки: (х, ŷ).

4) условие остановки: если все N точек перебраны в соответствии с подпунктами 2 и 3 ( кроме значений начальной БЗ), то построение модели заканчивается. Иначе переходим к шагу 2.

Параметры σ и d задаются до начала эксперимента.