24. Операции композиции нечетких отношений и нечеткой импликации, их значение для нечеткого логического вывода.

Композиция (свёртка) 2-х нечетких отношений. Допустим, R₁-нечеткое отнош-е м/у X и Y, R₂-нечеткое отнош-е м/у Y и Z. Нужно установить нечеткое отнош-е м/у X и Z. Свёрткой или композицией нечетких отношений R₁ и R₂ наз-ся нечеткое отношение, обозначаемое R₁оR₂ и определяемое выражением:

µ_R1оR2(х,z)=V[µ_R1(x,y) Λ µ_R2(y,z)]=max[min (µ_R1(x,y),µ_R2(y,z))]. Это наз-ют maxmin-ой композицией. Существ-ет композиция maxprod («Λ» заменяется алгебраич-м произвед-м множ-в).

Свойства (max-min)-композиции. Операция композиции ассоциативна, т.е. R₃о(R₂оR₁)=(R₃oR₂)oR₁, дистрибутивна от-но объединения, но не дистриб-на от-но пересечения: R₃о(R₂υR₁)=(R₃oR₂)υ(R₃оR₁),

R₃о(R₂∩R₁)<>(R₃oR₂)∩(R₃оR₁). Для max-min-композиции выпол-ся след-ее важное св-во: если R₁включ-ся в R₂, то RоR₁ включ-ся в RоR₂.

Импликация-это рассуждения типа «если p, то q»:

p->q. Н-р, р:Х=А, q:Y=B. Таблица истинности: (0, когда 1->0, в ост. случаях 1)

А: четырехугольник-квадрат

В:Около него можно описать окружность.

Под способом определения нечеткой импликации «если р, то q», где р и q- нечеткие множества, будем понимать способ задания нечеткого отношения R на базовых множествах PxQ, которые соответствуют высказыванию р->q.

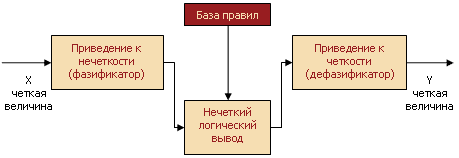
Как операцию композиции, так и операцию импликации в алгебре нечетких множеств можно реализ-ть по-разному, но в любом случае общий логич-ий вывод осущ-ся за след 4 этапа:

1. Нечеткость (введение нечеткости, фазификация). Ф-ции принад-ти, определ-ые на входных переменных применяются к их фактич-им значениям для определения степени истинности каждой предпосылки каж правила.

2. Логический вывод. Вычисленное значение истинности для предпосылок каждого правила примен-ся к заключениям каждого правила. Это приводит к одному нечеткому подмнож-ву, к-ое будет назначено каж переменной вывода для каж правила.В кач-ве правил лог-го вывода обычно исп-ются только операции min и prod. В лог-м выводе минимума ф-ция принадл-ти вывода «отсекается» по высоте, соответствующей вычисленной степени истинности предпосылки правила. В лог-м выводе умножения ф-ция принадл-ти вывода масштаб-ся при помощи вычисл-ой степени истинности предпосылки правила.

3. Композиция. Все нечеткие подмнож-ва, назначенные к каждой переменной вывода (во всех правилах), объедин-ся вместе,чтобы формир-ть одно нечеткое подмнож-во для каж переменной вывода. При таком объединении обычно исп-ся операции max и sum. При композиции максимума комбинированный вывод нечеткого подмнож-ва строится как поточечный максимум по всем нечетким подмнож-вам. При композиции суммы комбинир-ый вывод нечеткого подмнож-ва строится как поточечная сумма по всем нечетким подмнож-вам, назначенным переменной вывода правилами лог-го вывода.

Приведение к четкости (дефазификация), которое исп-ся, когда надо преобр-ть нечеткий набор выводов в четкое число.

25. Нечеткий логический вывод.

При обычном логическом выводе имеется набор жестких правил, сформулированных в понятиях алгебры логики. Все правила имеют вид импликации.

Пр₁: ЕСЛИ Х это A₁ ТО У это B₁ ……………. Прn: ЕСЛИ Х это An ТО У это Bn. Аналогично можно сформулировать набор правил в нечетком выводе. В этом случае будем иметь нечеткую импликацию, где степень истинности может принимать любое значения от 0 до 1.

Знание эксперта в форме А→В отражает нечеткое отношение посылки и заключения. В этом случае – результат нечеткого вывода, Ấ – предпосылка (например, наблюдение эксперта), R – нечеткое подмножество прямого произведения. Нечеткий вывод можно построить в виде: = Ấ○R= Ấ ○(А→В)

Вывод – это композиция нечеткого множества посылок и нечеткого отношения( знаний эксперта)

Общая схема: Входная переменная Х является нечетким подмножество А, входная переменная У является нечетким подмножество В,

Пусть в базе правил имеется m нечетких правил вида: R₁: ЕСЛИ x₁ это A₁₁ … И … x_n это A_1n, ТО y это B₁ … R_i: ЕСЛИ x₁ это A_i1 … И … x_n это A_in, ТО y это B_i … R_m: ЕСЛИ x₁ это A_i1 … И … x_n это A_mn, ТО y это B_m, где x_k , k=1..n – входные переменные; y – выходная переменная; A_ik – заданные нечеткие множества с функциями принадлежности.

Результатом нечеткого вывода является четкое значение переменной y^* на основе заданных четких значений x_k , k=1..n.

В общем случае механизм логического вывода включает следующие этапы:

1) фазификация – это искусственное введение нечеткости фактических данных, т.е. точное значение Х₀ интерпретируется, как нечеткие множества.

2) набор композиций: Х₀₁ ○ Аi1, ……. , Х₀n ○ Аin

Х_{01, ….,} Х₀n – подвергаются композиции i (1,…,m)

Означает степень пригодности каждого правила к нечеткой ситуации (Х₁=Х₀₁, Хn= Х₀n). Мерой пригодности является функция принадлежности (μ₁,μ₂,…,μm). В отличие от четкого логического вывода, здесь участвуют все правила сразу, причем влияние на результат соотносится со степенью их пригодности в сложившейся ситуации.

3) вычисление нечеткой импликации: (Х₁○Ai₁)^….^ (Хn○Ain) → Bi

Результатом является m нечетких значений для выхода В

4) агрегация – получение одного нечеткого множества путем объединения результатов предыдущих этапов, т.е. получение среднего значения.

5

)дефазификация – приведение к четкости, т.е. выбор четкого числа нечеткому значению выхода (В).