8. Оценка эксплуатационных свойств трансформаторов

8.1. Внешние характеристики трансформатора

Зависимости U_НН=f(k_нг), рассчитываем при питании обмотки ВН понижающего трансформатора номинальным напряжением, номинальной частоты при изменении величины симметричной нагрузки и заданном значении cosφ₂=const активно-индуктивной и активно-емкостной нагрузок.

Согласно заданному варианту при активно-индуктивной нагрузке cosφ₂=0,7 и при активно-емкостной нагрузке cos(-φ₂)=0,8.

При коэффициенте нагрузки трансформатора k_нг = 1,0:

- для активно-индуктивной нагрузки изменение напряжения трансформатора

%.

где u_а, u_р – расчетные значения активной и реактивной составляющих напряжения короткого замыкания, %;

при cosφ₂ = 0,7; sinφ₂ = √1-cosφ₂² = √1-0,7² = 0,714.

Фазное (линейное) напряжение обмотки НН

.

- для активно-емкостной нагрузки изменение напряжения трансформатора

%.

где при cos(-φ₂) = 0,8 => sin(-φ₂) = - √1-cos(-φ₂)² = - √1-0,8² = -0,6.

Фазное (линейное) напряжение обмотки НН

%.

Результаты расчета значения k_нг=0÷1,25 обоих характеров нагрузки приведены в таблице1.

Таблица 1 – Результаты расчетов внешних характеристик трансформатора

kнг		0	0,25	0,50	0,75	1,00	1,25
Активно-индуктивная сosφ2 = 0,7	ΔU,%	0.000	1.053	2.106	3.158	4.211	5.264
	UНН,%	100.000	98.947	97.894	96.842	95.789	94.736
Активно-емкостная сos(-φ2) = 0,8	ΔU,%	0.000	-0.199	-0.398	-0.597	-0.796	-0.995
	UНН,%	100.000	100.199	100.398	100.597	100.796	100.995

По результатам расчетов построим внешние характеристики трансформатора в одних осях координат ( рисунок 7).

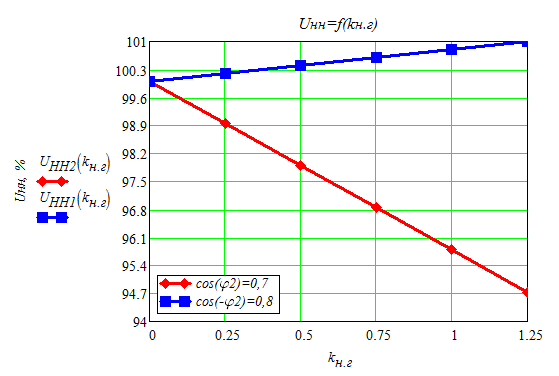
Рисунок 7 - Внешние характеристики трансформатора

ВЫВОД: изменение вторичного напряжения ΔU зависит от величины нагрузки и от характера этой нагрузки. Отрицательные значения ΔU при работе трансформатора с емкостной нагрузкой соответствует повышению напряжения с увеличением коэффициента нагрузки. Наибольшее изменение напряжения ΔU = 5,264% соответствует активно-индуктивной нагрузке при cosφ₂ = 0,7 и коэффициенту нагрузки k_нг = 1, т.к. длительная перегрузка трансформатора недопустима.

8.2. ЗАВИСИМОСТИ ΔU=f(φ₂)

Зависимости отклонения напряжения на клеммах вторичной обмотки от характера нагрузки при симметричной нагрузке двух заданных величин - ΔU=f(φ₂), рассчитываем при питании со стороны обмотки ВН номинальным напряжением номинальной частоты. Трансформатор работает при симметричной нагрузке неизменной величины. Расчет ведем для двух значений коэффициента нагрузки k_нг = 0,5; 1,0.

При коэффициенте нагрузки трансформатора k_нг = 0,5:

- при угле φ₂ = -30⁰ < 0; cosφ₂ = 0,866, sinφ₂ = -0,5

%.

- при угле φ₂ = 30⁰ > 0; cosφ₂ = 0,866, sinφ₂ = 0,5

%.

Результаты расчетов приведены в таблице 2.

Таблица 2 – Результаты расчетов зависимостей ΔU=f(φ₂)

ΔU = f(φ2)
φ2, град	-90	-75	-60	-45	-30	-15	0
kнг = 0,5	-1.980	-1.657	-1.221	-0.702	-0.135	0.442	0.988
kнг = 1,0	-3.960	-3.314	-2.442	-1.404	-0.269	0.883	1.975
φ2, град	90	75	60	45	30	15	0
kнг = 0,5	1.980	2.168	2.209	2.099	1.846	1.467	0.988
kнг = 1,0	3.960	4.337	4.418	4.197	3.691	2.933	1.975

По результатам расчетов построим зависимости ΔU=f(φ₂) в одних осях координат (рисунок 8).

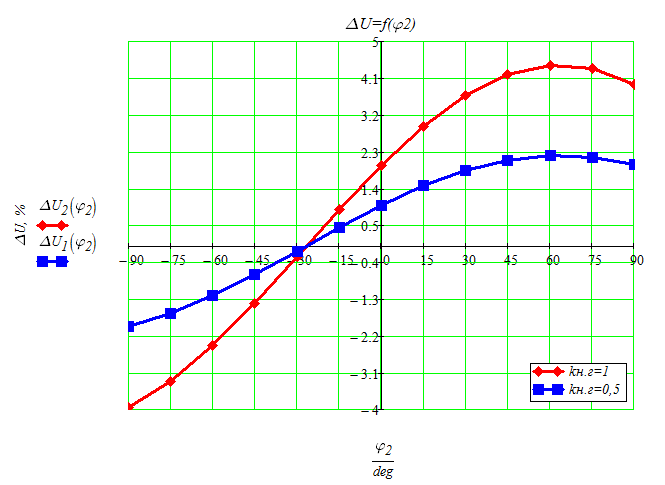
Рисунок 8 - Зависимости ΔU = f(φ₂)

ВЫВОДЫ: При φ₂ > 0 зависимости ΔU = f(φ₂) соответствуют смешанной активно-индуктивной нагрузке, а при φ₂ < 0 – активно-емкостной. При активно-индуктивной нагрузке вторичное напряжение трансформатора падает, а в случае активно-емкостной нагрузки при φ₂>0 оно повышается. Это обусловлено тем, что при протекании через индуктивное сопротивление индуктивный ток вызывает понижение напряжения, а емкостной ток – повышение.

8.3. ЗАВИСИМОСТИ η=f(k_нг)

Зависимости коэффициента полезного действия от величины симметричной нагрузки рассчитываем при питании со стороны обмотки ВН номинальным напряжение номинальной частоты, при заданном коэффициенте мощности (cosφ₂ = const) активно-индуктивного и активно-емкостного характера нагрузки.

Согласно заданному варианту при активно-индуктивной нагрузке cosφ₂ = 0,7 и при активно-емкостной нагрузке cos(-φ₂) = 0,8.

Трансформатор работает с максимальным коэффициентом полезного действия при коэффициенте нагрузки

.

Коэффициент полезного действия определяем по формуле

,

где Р_х – расчетное значение потерь холостого хода, кВт;

Р_к – расчетное значение потерь короткого замыкания, кВт.

Рассчитаем максимальное значение коэффициента полезного действия при k_нг = 0,438

Результаты расчетов приведены в таблице 3.

Таблица 3 – Результаты расчетов зависимостей η = f(k_нг)

kнг		0	0,25	0,494	0,50	0,75	1,00	1,25
активно-индуктивная нагрузка cosφ2 = 0,7	Рх, кВт	0.379	0.379	0.379	0.379	0.379	0.379	0.379
	kнг2Рк	0.000	0.123	0.379	0.494	1.111	1.975	3.087
	kнгSнсosφ2	0.000	17.500	30.648	35.000	52.500	70.000	87.500
	η,о.е.	0.000	0.972	0.976	0.976	0.972	0.967	0.962
активно-емкостная нагрузка cos(-φ2) = 0,8	Рх, кВт	0.379	0.379	0.379	0.379	0.379	0.379	0.379
	kнг2Рк	0.000	0.123	0.379	0.494	1.111	1.975	3.087
	kнгSнсosφ2	0.000	20.000	35.027	40.000	60.000	80.000	100.000
	η,о.е.	0.000	0.976	0.979	0.979	0.976	0.971	0.967

По результатам расчетов построим зависимости η=f(k_нг) в одних осях координат (рисунок 9).

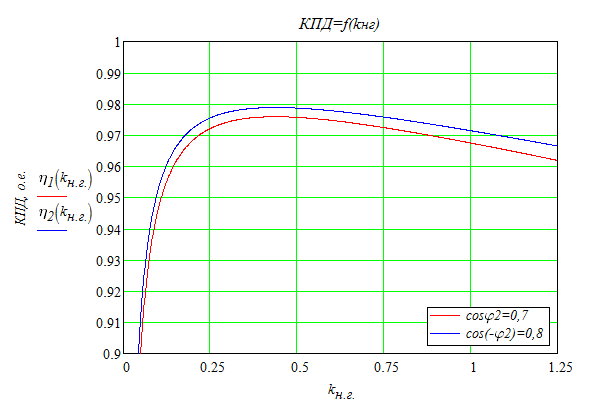
Рисунок 9 - Зависимости η = f(k_нг)

ВЫВОД: Коэффициент полезного действия трансформатора зависит от величины и от характера нагрузки. Чем больше активная составляющая нагрузки, тем больше коэффициент полезного действия. Максимальное значение коэффициента полезного действия соответствует коэффициенту нагрузки k_нг = 0,438.