
- •4. Некоторые вопросы алгебры
- •4.1. Матрицы и определители
- •4.1.1. Матрицы и операции над ними
- •4.1.2. Определители квадратных матриц
- •4.2. Матричная алгебра в решении задач с экономическим содержанием
- •4.3. Применение матриц в теории игр
- •4.3.1. Матричные игры двух игроков.
- •4.3.2. Алгоритм решения матричной игры (исследования игры)
- •4.4.Системы линейных уравнени
- •4.4.1. Понятие системы линейных уравнений и её решения
- •4 .4.2. Виды систем линейных уравнений Однородная система линейных уравнений
- •4.4.3. Методы решения систем линейных уравнений
- •Метод Гаусса
- •3. Матричный способ.
- •4.4.4. Системы линейных уравнений в решении практических задач
3. Матричный способ.
Этот способ решения
использует запись системы в виде
матричного уравнения
![]() .
где
– основная матрица системы,
.
где
– основная матрица системы,
 – матрица-столбец переменных,
– матрица-столбец переменных,
 – матрица-столбец свободных членов.
Если
,
то решение находится по формуле
– матрица-столбец свободных членов.
Если
,
то решение находится по формуле
![]() .
Поскольку решение системы сводится к
нахождению обратной матрицы, то этот
способ решения называют также методом
обратной матрицы
.
Поскольку решение системы сводится к
нахождению обратной матрицы, то этот
способ решения называют также методом
обратной матрицы
Задача 41.
Решить систему
 методом
обратной матрицы.
методом
обратной матрицы.
Решение.
Выпишем основную матрицу
и матрицу–столбец
для данной системы:
 ,
,
 .
Матрица переменных
.
Матрица переменных
 .
Тогда в матричной форме система имеет
вид
.
Определитель основной матрицы
.
Тогда в матричной форме система имеет
вид
.
Определитель основной матрицы
 поэтому обратная матрица
существует:
поэтому обратная матрица
существует:
 .
Теперь найдем
по формуле
.
Итак,
.
Теперь найдем
по формуле
.
Итак,

![]() .
.
Задачи.
Решите систему методом Гаусса
42.
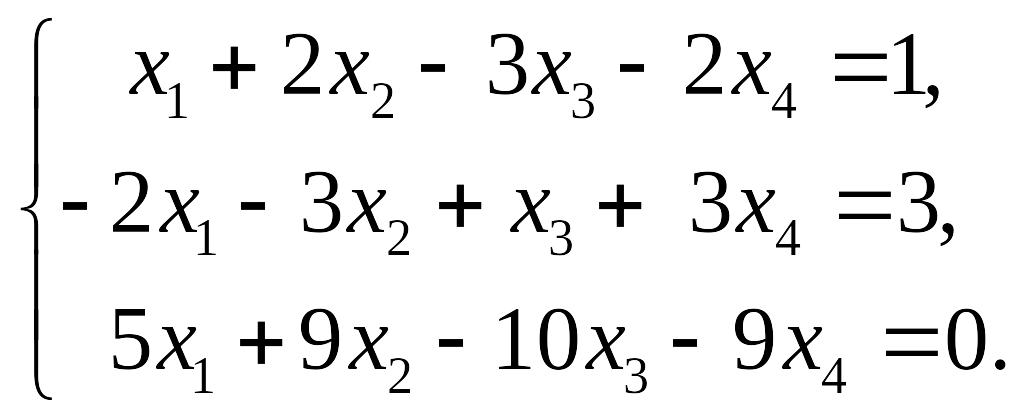
![]() 43.
43.
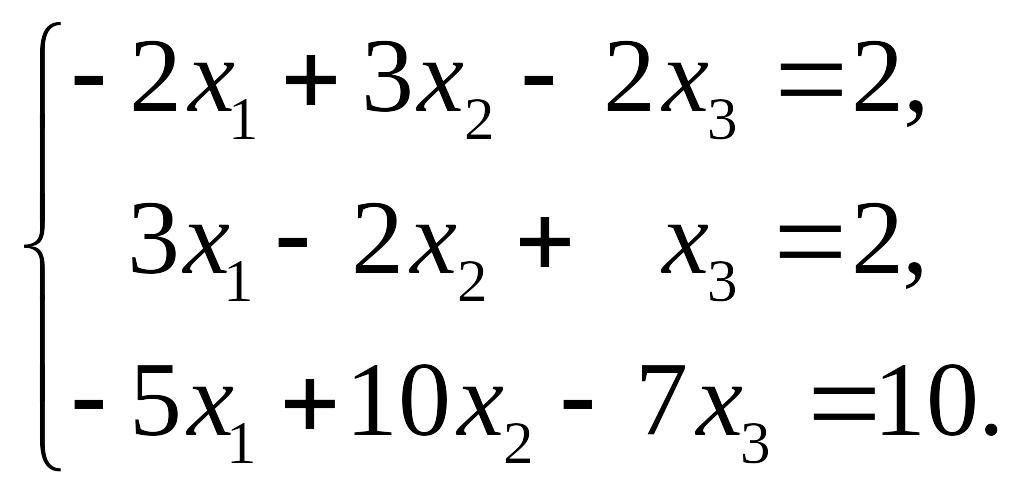
44.
 45.
45.
146.
 47.
47.
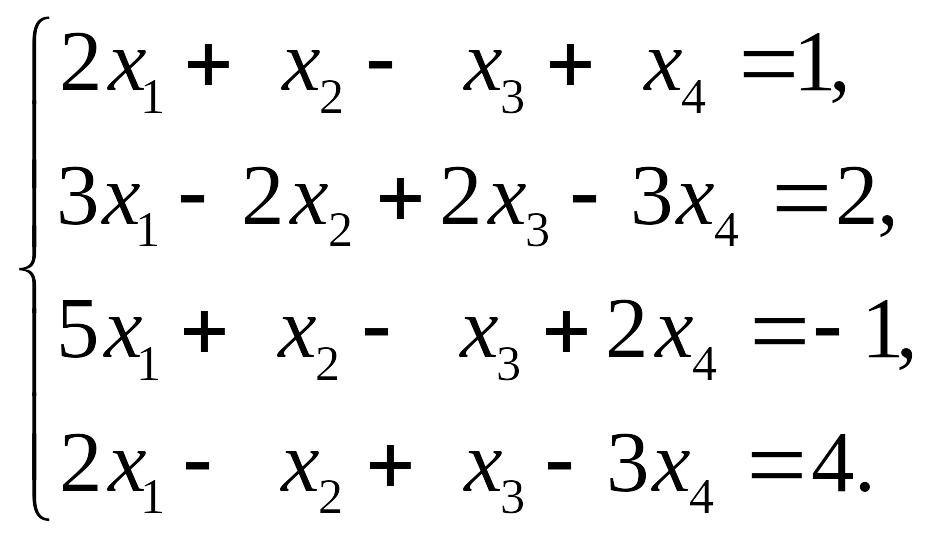
48.
 49.
49.

1.7.
![]() 1.8.
1.8.
![]()
По правилу Крамера решить системы линейных уравнений.
50.
51.

52.
 53.
53.

54.
 55.
55.
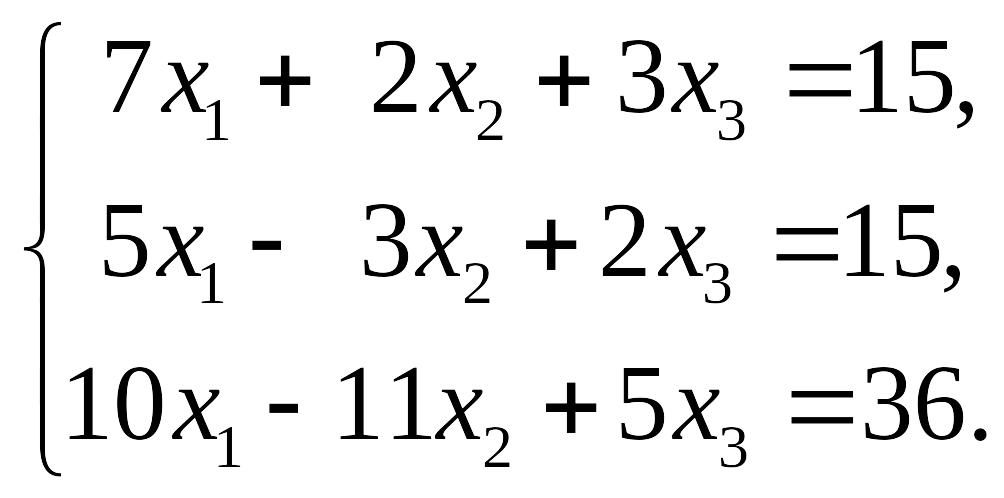
56.
 57.
57.
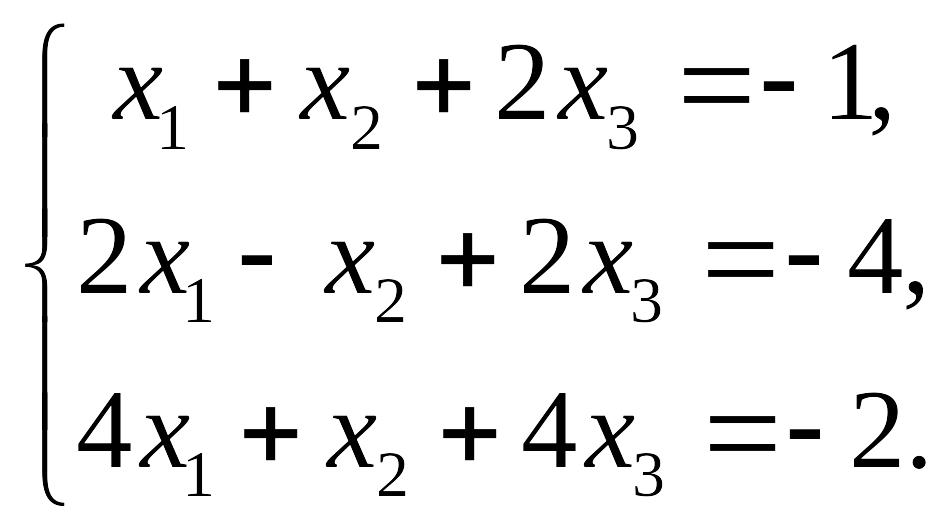
Решить систему методом обратной матрицы.
58. 59.
60.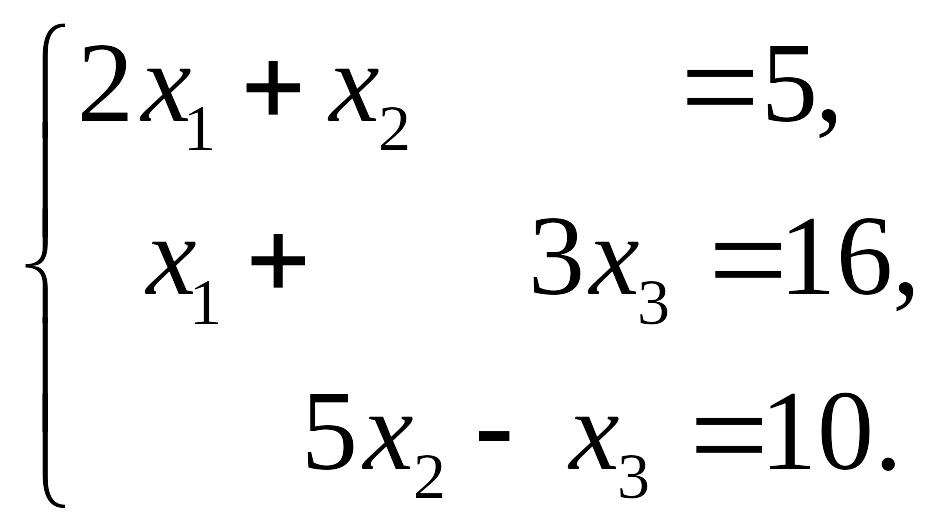 61.
61.
62.
 63.
63.

4.4.4. Системы линейных уравнений в решении практических задач
64. Швейная фабрика в течение трех дней производила костюмы, плащи и куртки. Известны объемы выпуска продукции каждого вида за три дня и денежные затраты на производство за эти дни:
-
День
Объем выпуска продукции
Затраты
(руб.)
Костюмы
Плащи Куртки
Первый
50
10
30
176
Второй
35
25
20
168
Третий
40
20
30
184
Найдите себестоимость продукции каждого вида.
Решение.
Пусть пошив одного костюма обходится
в
![]() руб., одного плаща –
руб., одного плаща –![]() руб., одной куртки
руб., одной куртки
![]() руб. Тогда затраты на производство в
первый день составят
руб. Тогда затраты на производство в
первый день составят
![]() (руб.), во второй день они будут составлять
(руб.), во второй день они будут составлять
![]() (руб.), а в третий день
(руб.), а в третий день
![]() (руб.). Таким образом, решение задачи
свелось к решению системы из трех
уравнений с тремя переменными:
,
(руб.). Таким образом, решение задачи
свелось к решению системы из трех
уравнений с тремя переменными:
,
,
.
Эта система равносильна следующей системе:
![]() ,
,
![]() ,
,
![]() .
.
Решая систему,
получим, что себестоимость костюма
![]() руб., себестоимость плаща
руб., себестоимость плаща
![]() руб., себестоимость куртки
руб., себестоимость куртки
![]() руб..
руб..
65. Фирма состоит из двух отделений, суммарная величина прибыли которых в минувшем году составила 12 млн. руб. На этот год запланировано увеличение прибыли первого отделения на 70%, а второго – на 40%.В результате суммарная прибыль должна вырасти в 1,5 раза.
Какова величина прибыли каждого отделения: а) в минувшем году; б) в этом году?
66. Имеются два раствора серной кислоты в воде: первый – сорокапроцентный, второй – шестидесятипроцентный. Эти два раствора смешали, после чего добавили 5 кг чистой воды и получили двадцатипроцентный раствор. Если бы вместо 5кг чистой воды добавили 5 кг восьмидесятипроцентного раствора, то получился бы семидесятипроцентный раствор. Сколько было сорокапроцентного и шестидесятипроцентного растворов?.
67. В редакции журнала работают 5 машинисток. Работая вместе, первая, вторая и третья могут напечатать рукопись за 7,5 часа; первая, третья и пятая – за 5 часов, первая, третья и четвертая – за 6 часов, вторая, четвертая и пятая – за 4 часа. Смогут ли они все вместе выполнить заказ в течение 3,5 часов?
1 Математический энциклопедический словарь. М., 1986., С. 140.
2 Хрестоматия по истории математики / под ред. А.П. Юшкевича, М.: Просвещение, 1976. С. 46.
