
- •4. Некоторые вопросы алгебры
- •4.1. Матрицы и определители
- •4.1.1. Матрицы и операции над ними
- •4.1.2. Определители квадратных матриц
- •4.2. Матричная алгебра в решении задач с экономическим содержанием
- •4.3. Применение матриц в теории игр
- •4.3.1. Матричные игры двух игроков.
- •4.3.2. Алгоритм решения матричной игры (исследования игры)
- •4.4.Системы линейных уравнени
- •4.4.1. Понятие системы линейных уравнений и её решения
- •4 .4.2. Виды систем линейных уравнений Однородная система линейных уравнений
- •4.4.3. Методы решения систем линейных уравнений
- •Метод Гаусса
- •3. Матричный способ.
- •4.4.4. Системы линейных уравнений в решении практических задач
4. Некоторые вопросы алгебры
4.1. Матрицы и определители
Понятие матрицы является одним из основных понятий алгебры. Оно широко используется не только в различных разделах математики, но и при решении различных экономических задач, в том числе, задач, связанных с теорией организации бизнеса, задач управленческого характера. В современных изданиях по экономике можно встретить такие понятия, как матричная карьера, матричная схема установки коэффициентов базового оклада, матричная схема формирования конкурентной карты рынка и т. д. В физике понятие матрицы применяют в электротехнике для описания электрических цепей (матрица инцидентности), для оценивания спектра сигналов, описания фильтрации сигналов. Используется понятие матрицы и при обработке различной статистической информации. Все это говорит о том, что понятие матрицы постепенно входит в словарь специалистов различных сфер деятельности.
4.1.1. Матрицы и операции над ними
Матрицей размером
![]() называется прямоугольная таблица чисел,
состоящая из
называется прямоугольная таблица чисел,
состоящая из
![]() строк и
строк и
![]() столбцов. Обозначают матрицы заглавными
буквами латинского алфавита:
столбцов. Обозначают матрицы заглавными
буквами латинского алфавита:
 .
.
Элемент, стоящий
в
![]() -ой
строке и
-ой
строке и
![]() -ом
столбце обозначают символом
-ом
столбце обозначают символом
![]() .
Первый индекс указывает на номер строки,
в которой находится элемент, а второй
– на номер столбца, в котором стоит этот
элемент. Элементы
.
Первый индекс указывает на номер строки,
в которой находится элемент, а второй
– на номер столбца, в котором стоит этот
элемент. Элементы
![]() образуют главную
диагональ
матрицы и называются диагональными.
Приведем примеры матриц:
образуют главную
диагональ
матрицы и называются диагональными.
Приведем примеры матриц:
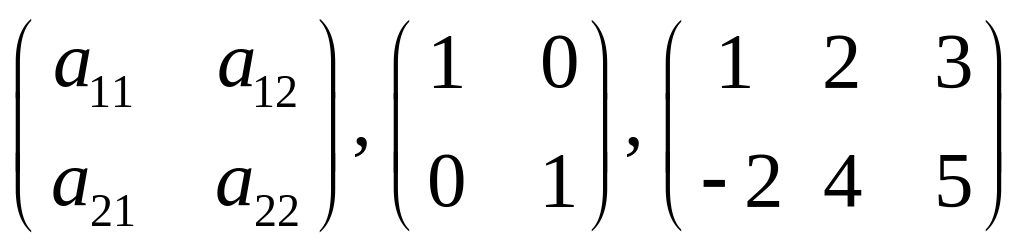 .
.
Матрица, у которой
число строк совпадает с числом столбцов
![]() ,
называется
квадратной
порядка
.
,
называется
квадратной
порядка
.
Матрица, все элементы которой равны 0, называется нулевой и обозначается символом 0.
Матрица вида
 ,
то есть квадратная матрица, все
недиагональные элементы которой равны
0, называется диагональной.
,
то есть квадратная матрица, все
недиагональные элементы которой равны
0, называется диагональной.
Диагональная
матрица, все диагональные элементы
которой равны 1, называется единичной
и обозначается символом
![]() ,
например, единичная матрица второго
порядка имеет вид:
,
например, единичная матрица второго
порядка имеет вид:
![]() .
.
Будем также рассматривать треугольные матрицы, у которых элементы, стоящие ниже или выше главной диагонали (или побочной диагонали), равны нулю, матрицы вида
 ,
,
где – любые действительные числа.
Операции над матрицами
Сложение и вычитание можно производить над матрицами, имеющими одинаковые размеры. Пусть
 и
и
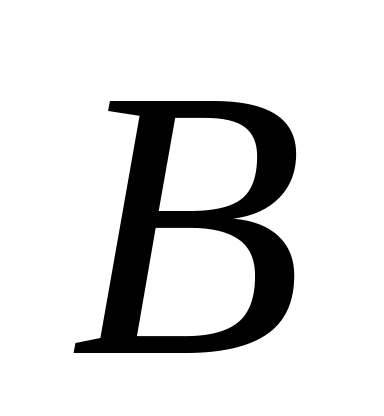 – матрицы размера
– матрицы размера
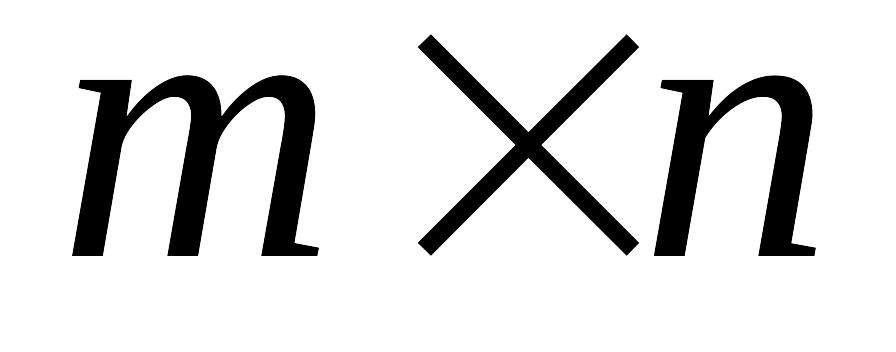 :
:
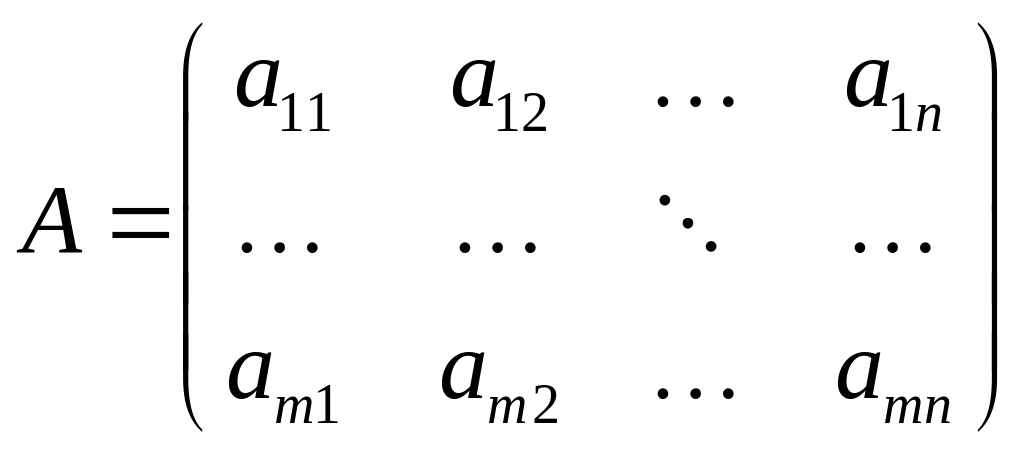 ,
,
 .
.
Суммой матриц одного размера называется матрица, элементы которой равны суммам соответствующих элементов матриц-слагаемых:
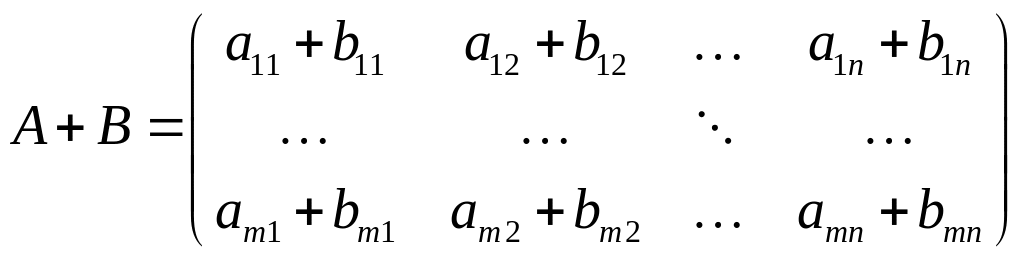 .
.
Произведением
матрицы на число
![]() называется
матрица, элементы которой равны
произведению всех элементов заданной
матрицы на число
:
называется
матрица, элементы которой равны
произведению всех элементов заданной
матрицы на число
:
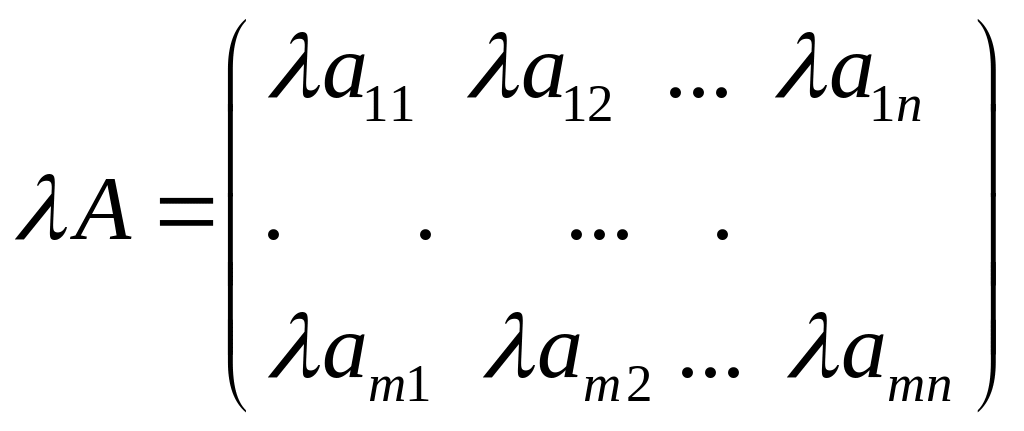 .
.
Операции сложения матриц и умножения матрицы на число удовлетворяют всем тем свойствам, которые имеют место для операций над действительными числами.
Две матрицы называются равными, если они имеют одинаковые размеры и их элементы, стоящие на одинаковых местах, равны:
(![]() )
)
![]()
![]() .
.
3. Умножение матрицы на матрицу не всегда возможно. Оно определяется только в том случае, если число столбцов первой матрицы равно числу строк второй.
Произведением
матрицы
![]() на матрицу
на матрицу
![]() называется
матрица
называется
матрица
![]() ,
каждый элемент
,
каждый элемент
![]() которой равен сумме произведений
элементов
-ой
строки матрицы
на
соответствующие
элементы
-ого
столбца матрицы
:
которой равен сумме произведений
элементов
-ой
строки матрицы
на
соответствующие
элементы
-ого
столбца матрицы
:
![]()
Иначе,
![]()
Следует заметить,
что для умножения матриц свойство
перестановочности не выполняется:
![]() .
.
Действительно,
если первое произведение существует,
то при этом второе может и не существовать.
Более того, существуют такие матрицы,
которые можно перемножить в любом
порядке, но при этом равенства произведений
![]() не будет.
не будет.
Единичная матрица
обладает свойством, аналогичным свойству
числа 1 во множестве чисел. Если
![]() –
матрица размера
,
то справа ее можно умножить на единичную
матрицу
-го
порядка и при этом
–
матрица размера
,
то справа ее можно умножить на единичную
матрицу
-го
порядка и при этом
![]() В то же время матрицу
можно умножить на единичную матрицу и
слева. Но в этом случае единичная матрица
должна иметь порядок
:
В то же время матрицу
можно умножить на единичную матрицу и
слева. Но в этом случае единичная матрица
должна иметь порядок
:
![]() .
.
4.
Транспонирование
матрицы
– это переход от матрицы
к матрице
![]() ,
в которой строки и столбцы матрицы
поменялись местами с сохранением порядка
следования:
,
в которой строки и столбцы матрицы
поменялись местами с сохранением порядка
следования:
![]() ,
,
![]()
Например, для
матрицы
![]() транспонированной будет матрица
транспонированной будет матрица
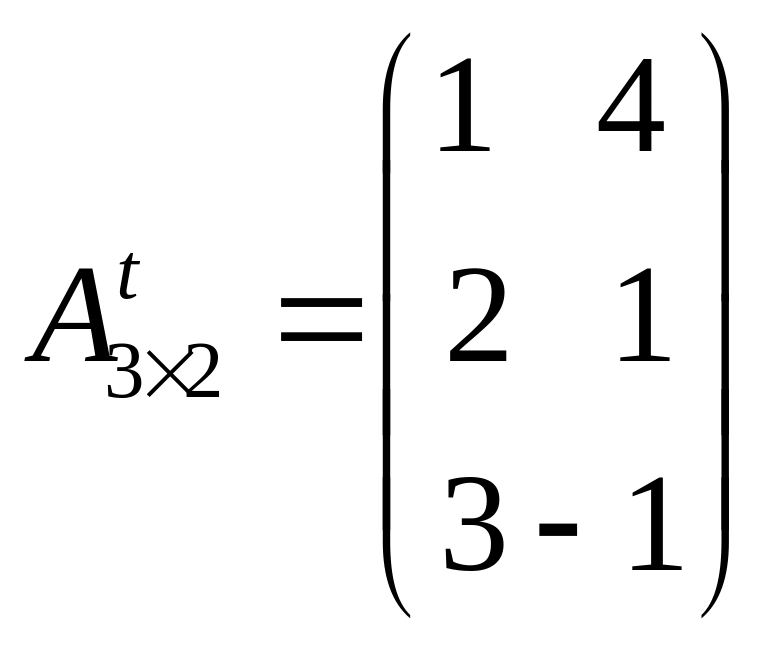 .
.
5. Матрица
![]() ,
обратная к квадратной
, – это матрица, удовлетворяющая условию
,
обратная к квадратной
, – это матрица, удовлетворяющая условию
![]() ,
где
– единичная матрица.
,
где
– единичная матрица.
Задачи.
1.
Указать, какие из следующих операций
можно выполнить, если
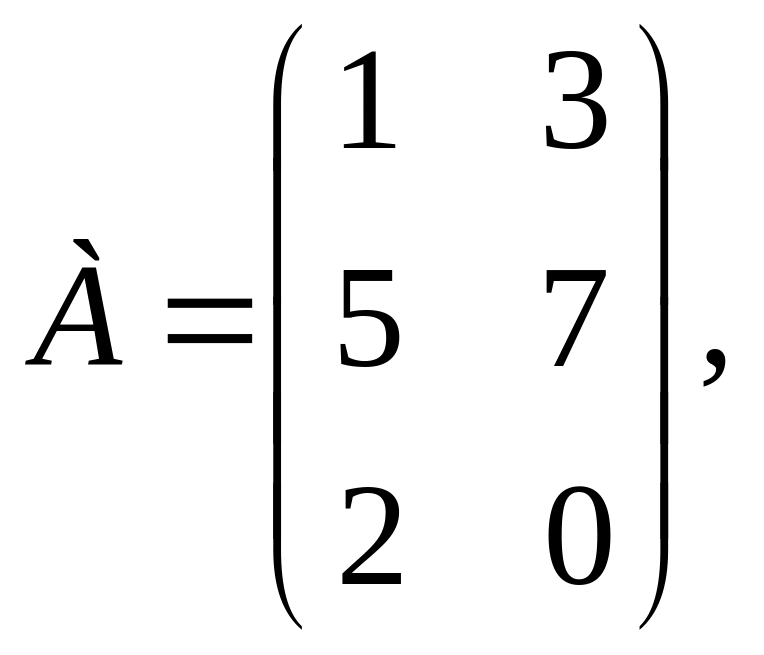 а
а
![]() :
а)
:
а)![]() ;
b)
;
b)
![]() ;
c)
;
c)![]() ;
d)
;
d)![]() ;
e)
;
e)
![]() ;
f)
;
f)![]() ;
g)
;
g)![]() ;
k)
;
k)![]() .
.
Решение. b)
Матрица
имеет размеры
![]() ,
тогда размеры транспонированной матрицы
равны
,
тогда размеры транспонированной матрицы
равны
![]() и совпадают с размерами матрицы
.
Значит, операция
выполнима и
+
=
и совпадают с размерами матрицы
.
Значит, операция
выполнима и
+
=![]() .
d)
Матрица
имеет размеры
,
а матрица
– размеры
.
Так как число столбцов первого сомножителя
совпадает с числом строк второго
сомножителя, то произведение
существует. Найдем это произведение –
матрицу
.
d)
Матрица
имеет размеры
,
а матрица
– размеры
.
Так как число столбцов первого сомножителя
совпадает с числом строк второго
сомножителя, то произведение
существует. Найдем это произведение –
матрицу
![]() размера
размера
![]() :
:
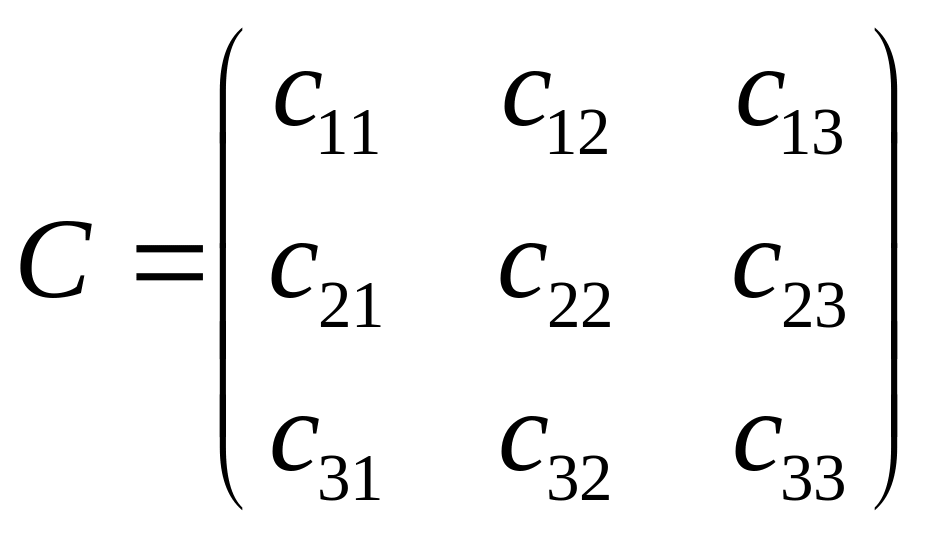 .
Согласно определению произведения
матриц для получения элементов первой
строки матрицы
.
Согласно определению произведения
матриц для получения элементов первой
строки матрицы
![]() рассмотрим первую строку матрицы
.
Элемент
рассмотрим первую строку матрицы
.
Элемент
![]() равен сумме произведений элементов
первой строки матрицы
на соответствующие элементы первого
столбца матрицы
:
равен сумме произведений элементов
первой строки матрицы
на соответствующие элементы первого
столбца матрицы
:
![]() ;
аналогично,
;
аналогично,
![]() ,
и
,
и
![]() .
.
Элементы второй строки матрицы находятся как суммы произведений элементов второй строки матрицы на соответствующие элементы первого, второго и третьего столбцов матрицы :
![]() ,
,
![]() ,
,
![]() .
.
Элементы третьей строки матрицы находятся умножением третьей строки матрицы на соответствующие элементы первого, второго и третьего столбцов матрицы :
![]() ,
,
![]() ,
,
![]() .
.
Все вычисления, производимые при умножении матриц, записывают следующим образом:
 .
.
2. Докажите, что операции сложения матриц и умножения матрицы на число удовлетворяет следующим свойствам:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() :
:
4) Для любой матрицы
существует матрица
![]() такая, что
такая, что
![]() .
.
Матрицу
![]() называют
матрицей противоположной
и обозначают символом (–
).
называют
матрицей противоположной
и обозначают символом (–
).
5)
![]() ;
;
6)
![]() ;
7)
;
7)
![]() ;
;
8)
![]() .
.
3.
Укажите, для каких пар матриц А и В
существуют произведения
![]() и
и
![]() :
a)
:
a)![]()
![]() ;
b)
;
b)![]()
![]() .
.
4.
Найдите произведение матриц: a)
![]() ; b)
; b)
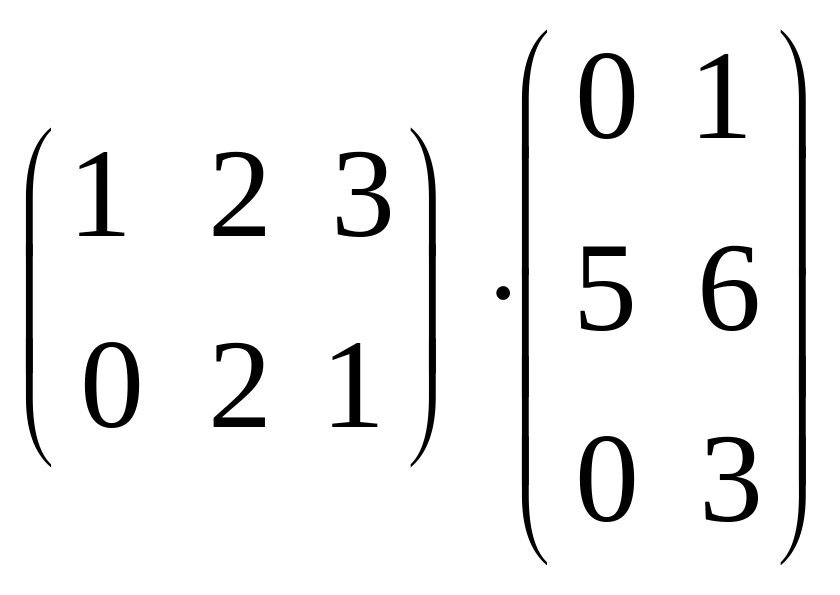 ;
;
c)
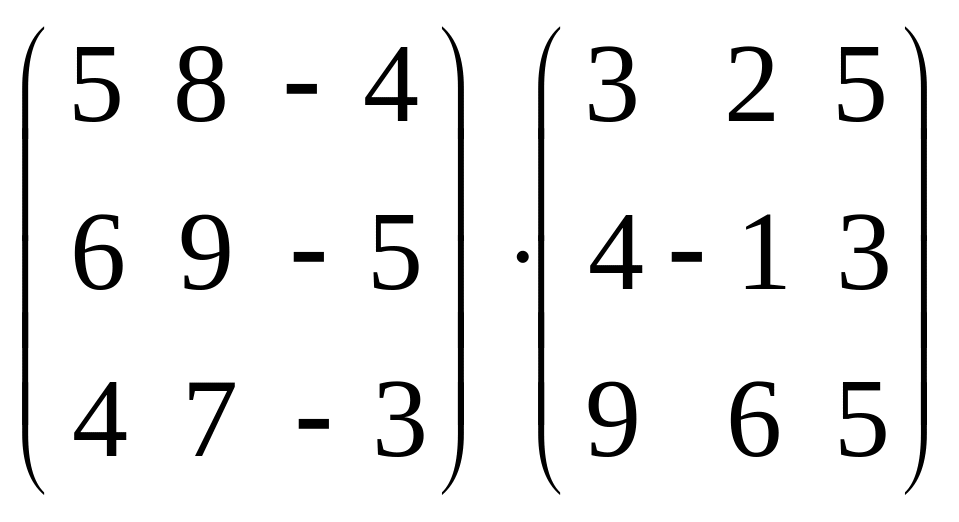 ;
d)
;
d)
 ;
e)
;
e) .
.
![]()
5. На примерах квадратных матриц второго порядка проверьте ваполнимость следующих свойств операции умножения матриц:
1)
![]() ,
,
2)
![]() ,
,
3)
![]() .
.
6.
Найдите матрицу 1)
![]() ,
2)
,
2)
![]() ,
если
,
если
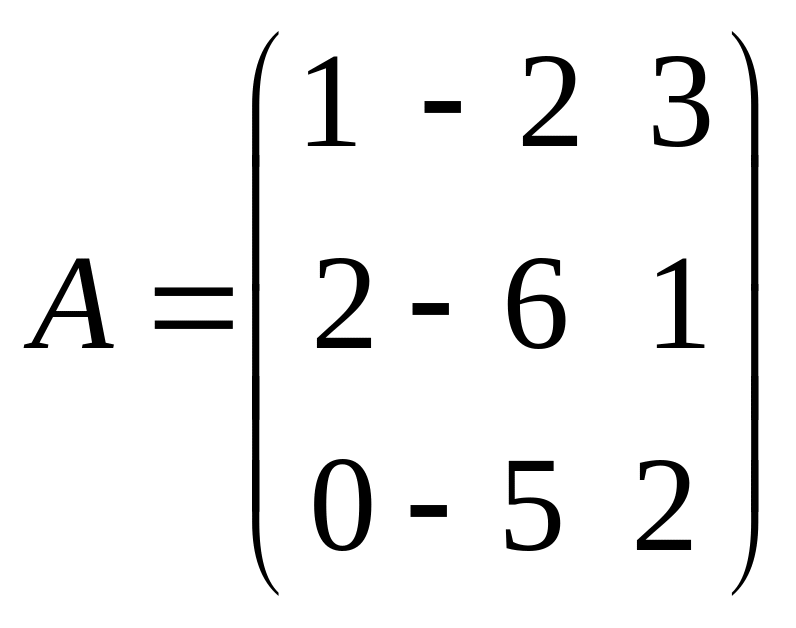 ,
,
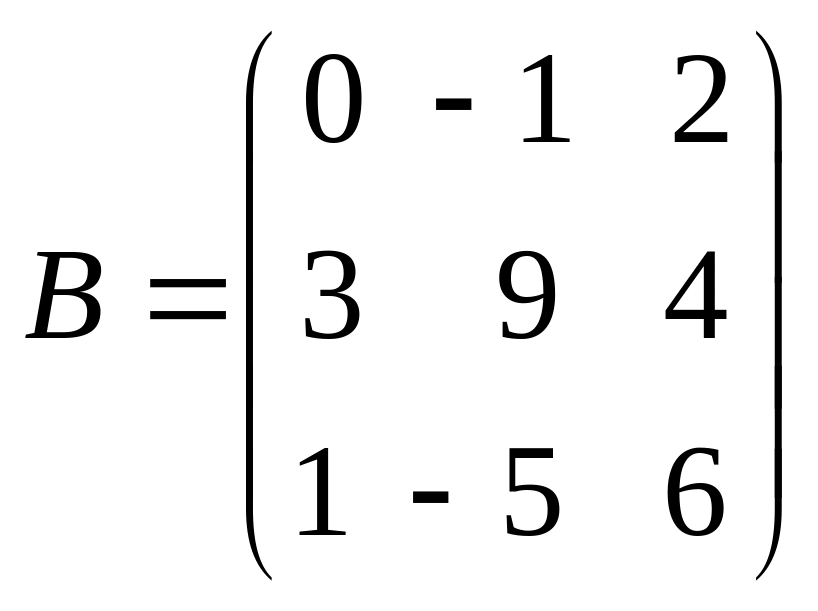 .
.
7.
Найдите значение многочлена 1)
![]() ,
2)
,
2)
![]() ,
если переменной
,
если переменной
![]() является матрица: a)
является матрица: a)
 ,
b)
,
b)
![]() .
.
Решение.( 1b)
Значение
многочлена 1) при
![]() равно
равно
![]() .
Будем
выполнять действия над матрицей
последовательно.
.
Будем
выполнять действия над матрицей
последовательно.
1.
![]()
![]()
![]() ;
2.
;
2.
![]()
![]()
![]() ;
3.
;
3.![]()
![]()
![]()
![]()
![]()
![]()
![]() +5
+5![]()
![]() .
.
Заметим, что число 5 обозначает здесь матрицу вида
![]()
![]() .
.
8. На матрицах третьего порядка проверьте выполнимость следующих свойств операции транспонирования:
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() .
.
9.
Проверьте, являются ли взаимно обратными
матрицы а)![]() и
и
![]() ;
б)
;
б)
![]() и
и
![]() .
.
Выясните, какие из приведенных ниже матриц имеют обратные:
а)
 ;
b)
;
b)
 ;
c)
;
c) ;
d)
;
d) .
.
11. Найдите матрицы, обратные заданным:
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
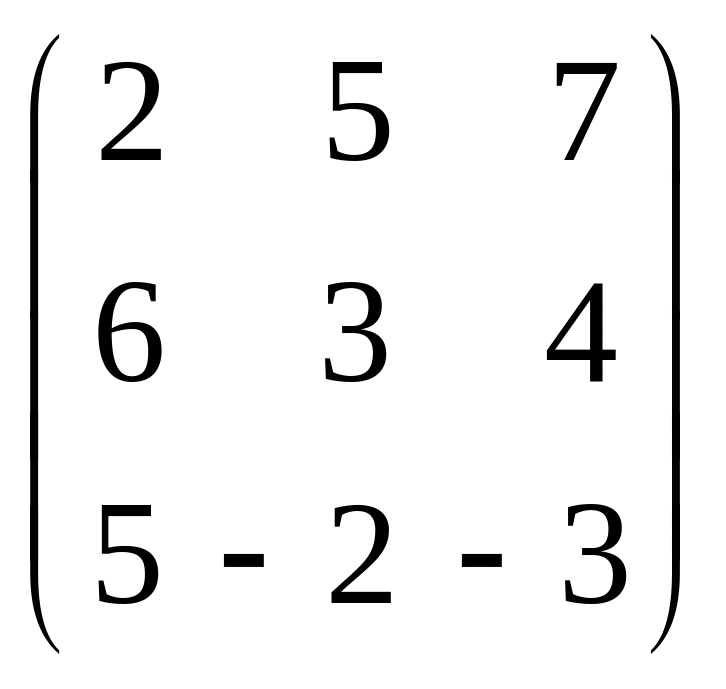 ;
4)
;
4)
 .
.
Для нахождения обратной матрицы используют так называемые элементарные преобразования матрицы. К ним относятся: 1) умножение строки матрицы на отличное от 0 число, 2) сложение строк, 3) сложение строки с другой строкой, умноженной на отличное от 0 число, 4) перестановка строк.
Решение. Найдем матрицу, обратную матрице 4). Для этого припишем справа к этой матрице единичную матрицу 3-его порядка и, используя элементарные преобразования, преобразуем полученную матрицу так, чтобы на месте данной матрицы оказалась матрица единичная, тогда на месте приписанной единичной матрицы будет стоять матрица, обратная к данной.


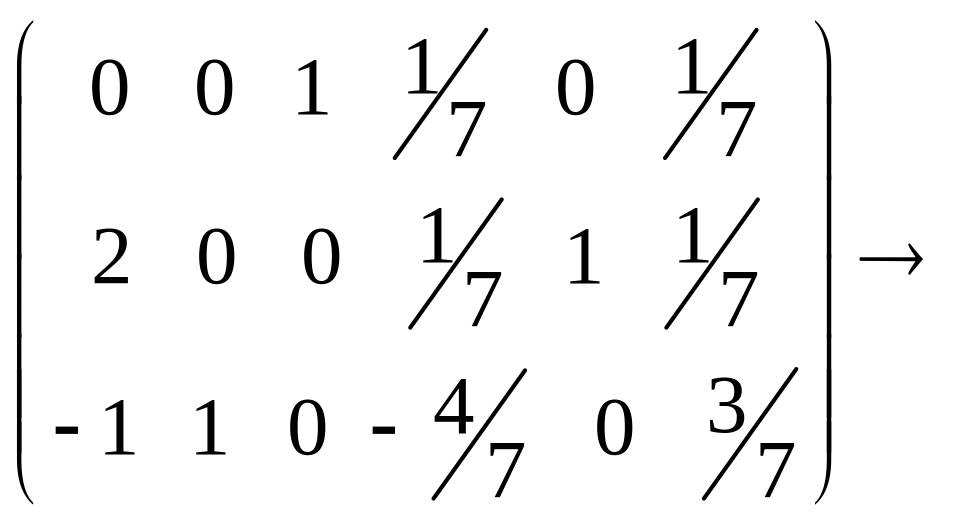
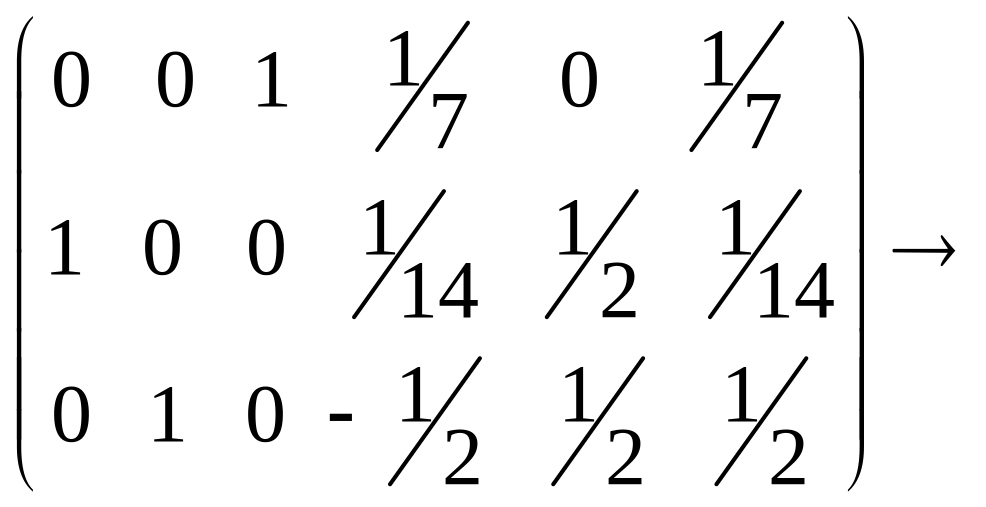
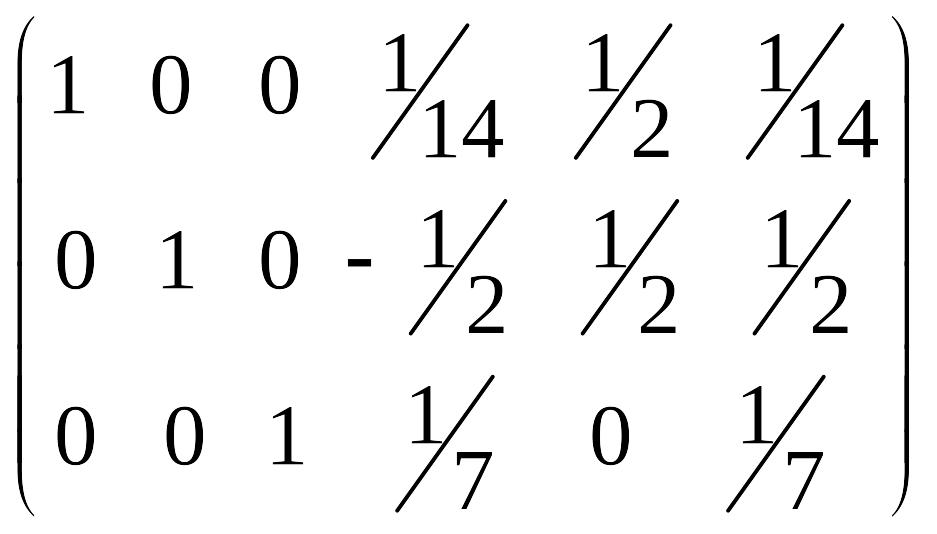 .
.
Поясним, как осуществляется переход к каждой последующей матрице. Вторая матрица получится, если первую строку исходной матрицы сложить с последней ее строкой.
Третья матрица получается делением первой строки второй матрицы на число 7.
Чтобы получить четвертую матрицу, надо выполнить две операции над строками третьей: 1) ко второй строке прибавить первую, 2) первую строку третьей матрицы умножить на (-4) и сложить с третьей ее строкой.
Пятая матрица получится, если: 1) вторую строку разделить на 2 , 2) вторую строку, деленную на 2, сложить с третьей.
Наконец переставляем строки так, чтобы на месте заданной матрицы стояла матрица единичная. Тогда обратной к данной матрице будет матрица
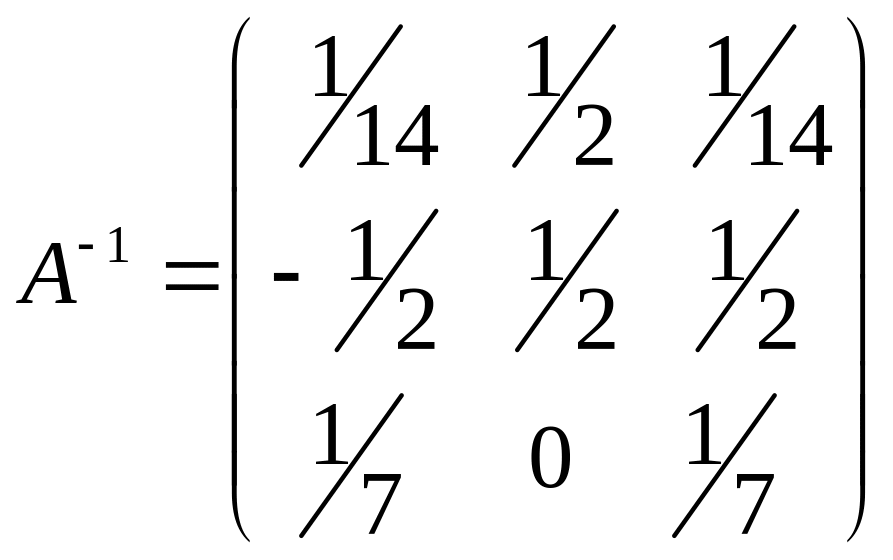 .
.
12.
Даны матрицы
![]() .
Найдите матрицу: а)
.
Найдите матрицу: а)![]() ;
;
b)
![]() ;
c)
;
c)
![]() .
.
13.
Найдите все матрицы, перестановочные
с матрицей
,
то есть матрицы
![]() ,
для которых выполняется условие
,
для которых выполняется условие
![]() :
:
а)
![]() ;
b)
;
b)
![]() ;
c)
;
c)
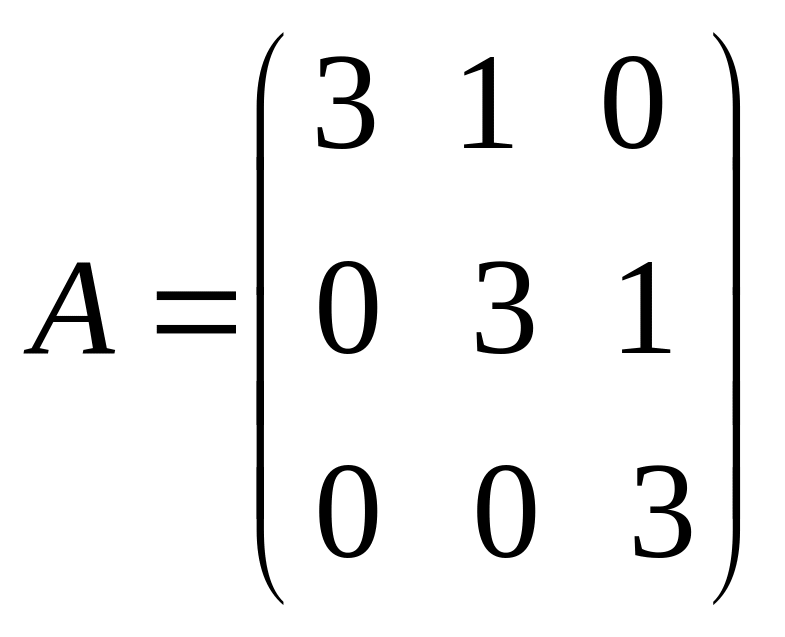 .
.
14. Найдите все матрицы второго порядка, квадрат которых равен нулевой матрице.
15. Найдите все матрицы второго порядка, квадрат которых равен единичной матрице.
