Дискретные геометрические модели.

Перечисление по пространственной занятости- это специальный случай разбиения на ячейки, в которой твердое тело разбивается на идентичные ячейки, называемые вокселами, располагающиеся в фиксированном регулярном порядке, по аналогии с пикселами. Наиболее используемый тип ячейки - куб. Чтобы представить объект, каждый воксель считается либо “занятым”, либо - нет. Ясно, что в общем случае тела аппроксимируются; нет понятия частичной занятости вокселов; высоки требования к памяти. Тем не менее, это ведущее представления для экспериментальных данных (volumetric data), в частности, в биомедицинских (томография ) исследованиях.

Функциональное представление геометрических объектов. Понятие об r-функциях. Теоретико-множественные операции и биективные преобразования.

Неравенство (1) описывает подпространство в n-мерном эвклидовом пространстве. Равенство определяет сложную функцию n-1 переменной и описывает ориентированную поверхность размерности n-1. В трехмерном случае, объект, определенный неравенством обычно называется твердым телом (или объемом), а объект, определенный равенством называется сложной поверхностью. Функциональное представление объемов и поверхностей применяется для описания геометрии твердых тел, компьютерном дизайне, анимации, обработки рядов и объемной графики.

Определим геометрический концепт как тройка: (M, Ф, W), где M – набор геометрических объектов, Ф – набор геометрических операций и W – набор отношений между наборами объектов. С точки зрения математики такой набор есть алгебраическая система. Рассмотрим основные части этой тройки.

Два основных типа набора М – это простые геометрические объекты (примитивы) и комплексные геометрические объекты. Геометрический примитив описывается отдельно взятой функцией, выбранной из конечного набора возможных типов. Комплексный геометрический объект является результатом набора операций над примитивами. В системе моделирования, конечный набор примитивов может быть определен. Однако должна быть обеспечена возможность расширения этого набора в символьной манере.

Набор геометрических операций Ф включает такие операции, что , где n – число операндов в операции. Результатом операции является также объект из набора M, который обеспечивает замкнутость функционального представления. Пусть объект G₁ определен как . Для унарных операций объект говорят, что объект G₂ получен из объекта G₁ так, что G₂=Ф_i(G₁) и определен как , где непрерывная вещественная функция одной переменной. Примерами унарных операций может служить афинное преобразование, проекции, оффсетинг. Для бинарных операций говорят, что объект G₃ получен из G₁ и G₂ так, что G₃=Ф_i(G₁,G₂) и определен как , где непрерывная вещественная функция двух переменных. Примерами бинарных операций являются теоретико-множественные операции, блендинг. Теоретико-множественные операции определяются в аналитическом виде с помощью разработанной В.Л.Рвачевым теории R-функций. При этом результирующий объект включает граничные точки, что соответствует операциям трехзначной логики над предикатом принадлежности точки. Существует несколько систем R-функций, каждая из которых имеет свойство замкнутости. Наиболее часто используется следующая система:

для объединения , для пересечения . Здесь  =  (f₁,f₂) - произвольная непрерывная функция такая, что: -1 < (f1,f2)  1, (f1,f2) = (f2,f1) = (-f1,f2) = (f1,-f2); для вычитания . На практике используют два важных частных случая:=1; в этом случае , . Основное ограничение этих широкоизвестных минимаксных операций заключается в разрывности С¹ в точках, где f₁ = f₂, что может вызвать нежелаемые результаты при последующих операциях над объектом.=0; в этом случае , . R-функции могут быть использованы для определения геометрических примитивов. Теоретико-множественные операции гладкого сопряжения (блендинг) генерируют сглаженные ребра конструктивных твердых тел с добавленным или удаленным материалом. Где R – соответствующая R-функция, d – функция смещения, принимающая максимальное значение d(0,0) и асимптотически стремится к нулю при увеличении значений ее аргументов. В частности, для d может быть предложено следующее выражение: 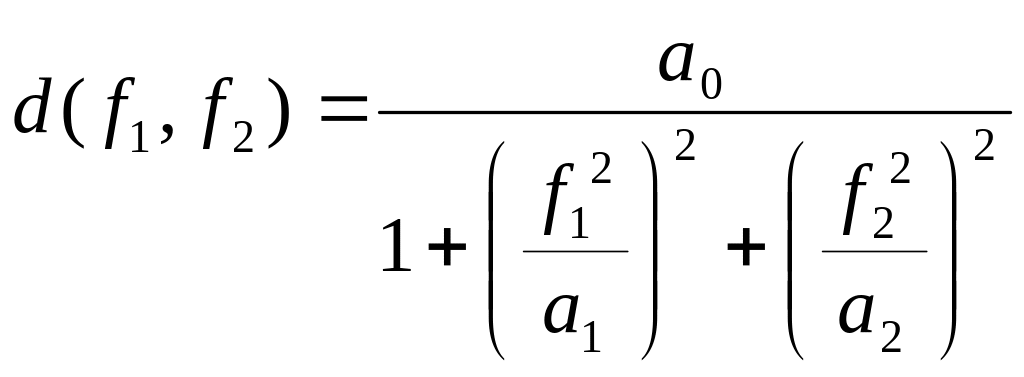, где a₀, a₁, a₂ – параметры, управляющие результирующей формой. Оффсетинг расширяет или сужает исходный объект. Виды: 1) Оффсетинг постоянного значения с F = f(X)+C, где отрицательная константа С характеризует отрицательный офсет, а положительная С – положительный офсет. 2) Оффсетинг вдоль нормали с F = f(X+DN) для положительного и F = f(X-DN) для отрицательного оффсетинга, где D – значение отклонения, а N – вектор градиента функции f в точке Х. 3) Оффсетинг постоянного радиуса с F = max(f(X’)) для положительного и F = max(f(X’)) для отрицательного оффсетинга, где Х’ – вектор координат точек, принадлежащих сфере данного радиуса D и с центром в точке X. Биективное отображение служит для определения деформаций исходных объектов. Пусть Ф_i определяется преобразованием координат: , где - непрерывная вещественная функция. Предполагаем, что существует обратная функция . Получающийся в результате объект описывается как : . Примеры таких преобразований: изгиб, кручение, сжатие-расширение, а также отображение из цилиндрической в декартову систему координат. Афинные преобразования – важный частный случай биективного отображения. Пусть Ф_i – афинное отображение, определенное равенством X’=AX+C, где , , , и А={a_ij} – это матрица преобразования размерностью n*n и ненулевым определителем. Тогда . Это может быть движение вдоль прямой, вращение или масштабирование во времени. R-функции могут быть также использованы для приблизительного описания операции проекции из Eⁿ в E^n-1, не использующее обратное преобразование Ф^-1. Пусть будет определение функции для сечения. Тогда определение функции для проекции с может быть определено как f₂=f₁₁|f₁₂|…|f_1j|…|f_1N. Декартово произведение - это операция, увеличивающая размерность. , где и n=k+m. При помощи R-функций: . Метаморфозис - это бинарная операция над объектами, определенными в пространстве E^n-1. Результирующий объект определен в Eⁿ и описывается как взвешенная интерполяция между двумя определяющими функциями f₁ и f₂: , где g(x_n) - положительная непрерывная функция, g(x_n0) = 0, g(x_n1) = 1.

Преимущества функционального представления как основы для интерактивной системы моделирования:

1) Простота спецификации. Функциональное представление является замкнутым, единообразным, расширяемым.

2) Изображательность. F-rep рассматривается как используемый для обеспечения быстрой визуализации данных пользователя. Это достигается с помощью преобразования в полигональную сетку. Алгоритм полигонизации может быть разложен на отдельные составляющие для распараллеливания вычислений. Компактность F-rep позволяет запустить программы вывода изображений на машинах с не очень большим объемом распределенной памяти (как, например, транспьютеры).

3) Анализируемость. Для функционального представления достаточно просто применять геометрические запросы, как, например включение точки. Оно позволяет вычислять физические величины относительно формы (объемы, моменты инерции) при помощи известных алгоритмов.

Основные алгоритмы визуализации

Базовые алгоритмы растровой развертки.

Поскольку экран растрового дисплея с электронно-лучевой трубкой (ЭЛТ) можно рассматривать как матрицу дискретных элементов (пикселей), каждый из которых может быть подсвечен, нельзя непосредственно провести отрезок из одной точки в другую. Процесс определения пикселей, наилучшим образом аппроксимирующих заданный отрезок, называется разложением в растр. В сочетании с процессом построчной визуализации изображения он известен как преобразование растровой развертки. Для горизонтальных, вертикальных и наклоненных под углом 45°. отрезков выбор растровых элементов очевиден. При любой другой ориентации выбрать нужные пиксели труднее. Общие требования к изображению отрезка:

• концы отрезка должны находиться в заданных точках;

• отрезки должны выглядеть прямыми,

• яркость вдоль отрезка должна быть постоянной и не зависеть от длины и наклона.

Ни одно из этих условий не может быть точно выполнено на растровом дисплее в силу того, что изображение строится из пикселей конечных размеров, а именно:

• концы отрезка в общем случае располагаются на пикселях, лишь наиболее близких к требуемым позициям и только в частных случаях координаты концов отрезка точно совпадают с координатами пикселей;

• отрезок аппроксимируется набором пикселей и лишь в частных случаях вертикальных, горизонтальных и отрезков под 45^ они будут выглядеть прямыми

• яркость для различных отрезков и даже вдоль отрезка в общем случае различна, так как, например, расстояние между центрами пикселей для вертикального отрезка и отрезка под 45^ различно

Алгоритмы генерации отрезка:

1. Цифровой дифференциальный анализатор. Решается дифференциальное уравнение вида dY/dX = Py/Px, где Py = Yk - Yn - приращение координат отрезка по оси Y, а Px = Xk - Xn - приращение координат отрезка по оси X. При этом ЦДА формирует дискретную аппроксимацию непрерывного решения этого дифференциального уравнения. В обычном ЦДА, используемом, как правило, в векторных устройствах, тем или иным образом определяется количество узлов N, используемых для аппроксимации отрезка. Затем за N циклов вычисляются координаты очередных узлов. Получаемые значения X_i, Y_i преобразуются в целочисленные значения координаты очередного подсвечиваемого пикселя либо округлением, либо отбрасыванием дробной части. Генератор векторов, использующий этот алгоритм, имеет тот недостаток, что точки могут прописываться дважды, что увеличивает время построения. Кроме того из-за независимого вычисления обеих координат нет предпочтительных направлений и построенные отрезки кажутся не очень красивыми.

2. Алгоритм Брезенхема. Так как приращения координат, как правило, не являются целой степенью двойки, то в ЦДА-алгоритме требуется выполнение деления, что не всегда желательно, особенно при аппаратной реализации. Брезенхем предложил алгоритм, не требующий деления, как и в алгоритме несимметричного ЦДА, но обеспечивающий минимизацию отклонения сгенерированного образа от истинного отрезка, как в алгоритме обычного ЦДА. Основная идея алгоритма состоит в том, что если угловой коэффициент прямой < 1/2, то естественно точку, следующую за точкой (0,0), поставить в позицию (1,0) (рис. а), а если угловой коэффициент > 1/2, то - в позицию (1,1) (рис. б). Для принятия решения куда заносить очередной пиксел вводится величина отклонения Е точной позиции от середины между двумя возможными растровыми точками в направлении наименьшей относительной координаты. З 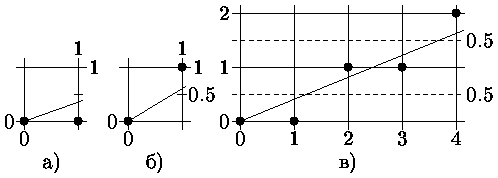нак Е используется как критерий для выбора ближайшей растровой точки. Если Е < 0, то точное Y-значение округляется до последнего меньшего целочисленного значения Y, т.е. Y-координата не меняется по сравнению с предыдущей точкой. В противном случае Y увеличивается на 1.

3. Модифицированный алгоритм Брезенхема. Основная идея алгоритма состоит в том, чтобы для ребер многоугольника устанавливать яркость пикселя пропорционально площади пикселя, попавшей внутрь многоугольника.

Одной из уникальных характеристик растрового графического устройства является возможность представления сплошных областей. Генерацию сплошных областей из простых описаний ребер или вершин будем называть растровой разверткой сплошных областей, заполнением многоугольников или заполнением контуров. Для этого можно использовать несколько методов, которые обычно делятся на 2 категории: растровая развертка и затравочное заполнение.

В методах растровой развертки пытаются определить в порядке сканирования строк, лежит ли точка внутри многоугольника или контура. Эти алгоритмы обычно идут от "верха" многоугольника к "низу".

В методах затравочного заполнения предполагается, что известна некоторая точка (затравка) внутри замкнутого контура. В алгоритмах ищут точки, соседние с затравочной и расположенные внутри контура. Если соседняя точка расположена не внутри контура, то значит, обнаружена граница контура. Если же точка расположена внутри контура, то она становится затравочной точкой и поиск продолжается рекурсивно. Подобные алгоритмы применимы только к растровым устройствам.

Многие замкнутые контуры являются простыми многоугольниками. Ели контур состоит из кривых линий, то его можно аппроксимировать подходящим многоугольником или многоугольниками. Простейший метод заполнения многоугольника состоит в проверке на принадлежность внутренности многоугольника каждого пиксела в растре. Этот методслишком расточителен. Затраты можно уменьшить путем вычисления для многоугольника прямоугольной оболочки - наименьшего многоугольника, содержащего внутри себя многоугольник.