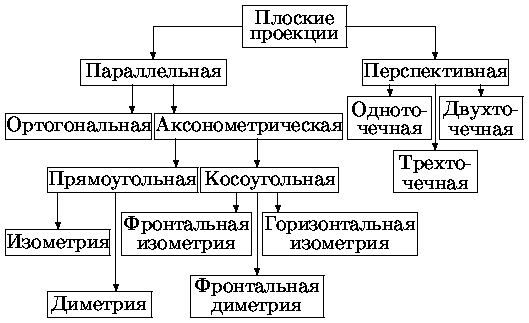
Плоские проекции трехмерных объектов. Математическое описание и классификация параллельных проекций.
При параллельной проекции центр проекции находится на бесконечном расстоянии от плоскости проекции. Проекторы представляют собой пучок параллельных лучей. В этом случае необходимо задавать направление проецирования и расположение плоскости проекции. По взаимному расположению проекторов, плоскости проекции и главных осей координат различаются ортогональные, прямоугольные аксонометрические и косоугольные аксонометрические проекции.
При ортогональной проекции проекторы перпендикулярны плоскости проекции, а плоскость проекции перпендикулярна главной оси. Т.е. проекторы параллельны главной оси.
При аксонометрической проекции имеется одна из двух перпендикулярностей:
при прямоугольной аксонометрической проекции проекторы перпендикулярны плоскости проекции, которая расположена под углом к главной оси;
при косоугольной аксонометрической проекции проекторы не перпендикулярны плоскости проекции, но плоскость проекции перпендикулярна к главной оси.
Изображение, полученное при параллельном проецировании, не достаточно реалистично, но передаются точные форма и размеры, хотя и возможно различное укорачивание для различных осей.
Плоские проекции трехмерных объектов. Математическое описание и классификация центральных проекций.
П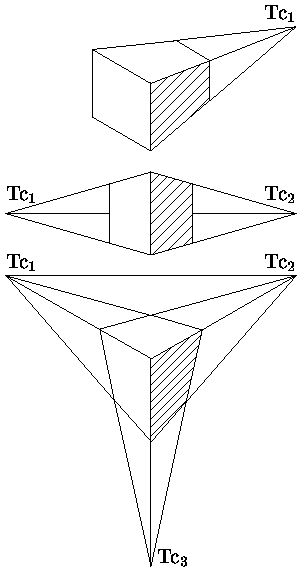
ри
центральной
проекции
расстояние
от центра проекции до плоскости
проецирования конечно, поэтому проекторы
представляют собой пучок лучей, исходящих
из центра проекции. В этом случае надо
задавать расположение и центра проекции
и плоскости проекции. Изображения на
плоскости проекции имеют т.н. перспективные
искажения, когда размер видимого
изображения зависит от взаимного
расположения центра проекции, объекта
и плоскости проекции. Из-за перспективных
искажений изображения, полученные
центральной проекцией, более реалистичны,
но нельзя точно передать форму и размеры.
Различаются одно, двух и трехточечные
центральные проекции в зависимости от
того по скольким осям выполняется
перспективное искажение.
Ниже приведена классификация описанных выше плоских проекций.
Конвейер видовых преобразований в двумерной графике.
Примитивы обычно задаются в системе мировых координат с использованием любых значимых для прикладной программы единиц измерений - от ангстремов и микрон до световых лет. Сам термин “мир” означает “реальный” мир, независимый от связанных с компьютером устройств. Экран дисплея имеет собственную систему координат - экранных или - в более универсальной формулировке - приборных координат, где измерения могут быть в пикселях. Для получения изображения сцены реального мира необходимо определить процедуру отображения некоторой прямоугольной области в системе мировых координат, называемой окном в мировых координатах в область или окно просмотра в системе приборных координат, называемую окно вывода. Такое отображающее преобразование применяется к каждому примитиву. Если окно в мировых координатах и окно вывода имеют разные отношения высота/ширина, то получается неоднородное масштабирование, искажающее пропорции. Может быть определено несколько вьюпортов одновременно - и даже на одном экране.
Шаги преобразования:
1. Окно в мировых координатах, заданное координатами левого нижнего и правого верхнего углов, сдвигается в начало координат;
2. Размер окна масштабируется чтобы совпал с размерами окна вывода;
3. Полученное окно переносится в заданную позицию окна вывода.
Результирующая матрица преобразований получается композицией двух матриц переноса и одной – масштабирования.
Если имеем точку в мировых координатах P [ x y 1 ]T, то соответствующая точка в приборных координатах будет:
P’ = Mwv P
= [ (x-xmin)*((umax-umin)/(xmax-xmin))+umin (y-ymin)*((vmax-vmin)/(ymax-ymin))+vmin 1 ].
Конвейер видовых преобразований в 3D графике.
В 2D - пространстве видовое преобразование было простым: объекты двумерного мира отсекались окном и затем преобразовывались во окно вывода для вывода на дисплей. 3D видовое преобразование усложняется дополнительной размерностью, от которой надо избавиться - для вывода на то же окно вывода на 2D видовую поверхность.
См. концептуальную схему.