Геометрические преобразования в 2d и 3d графике.
Изменение масштаба. Диагональные элементы основной матрицы преобразования 4х4 осуществляют частичное и полное изменение масштабов. Рассмотрим преобразование
,
которое производит частичное изменение масштабов. Общее изменение масштаба получается за счет использования
четвертого диагонального элемента, т. е.
.
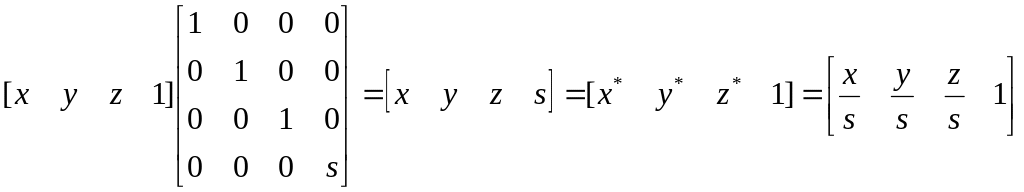
Такой же резуль-тат можно получить при равных коэффициентах частичных изменений масштабов. В этом случае матрица преобразования должна быть равной
Сдвиг. Матрица сдвига имеет вид. Матрица обратного преобразования получается путем замены знака у Tx, Ty, Tz.
Вращение. Если определитель матрицы 3х3 равен +1, то имеет место чистое вращение около начала координат.
П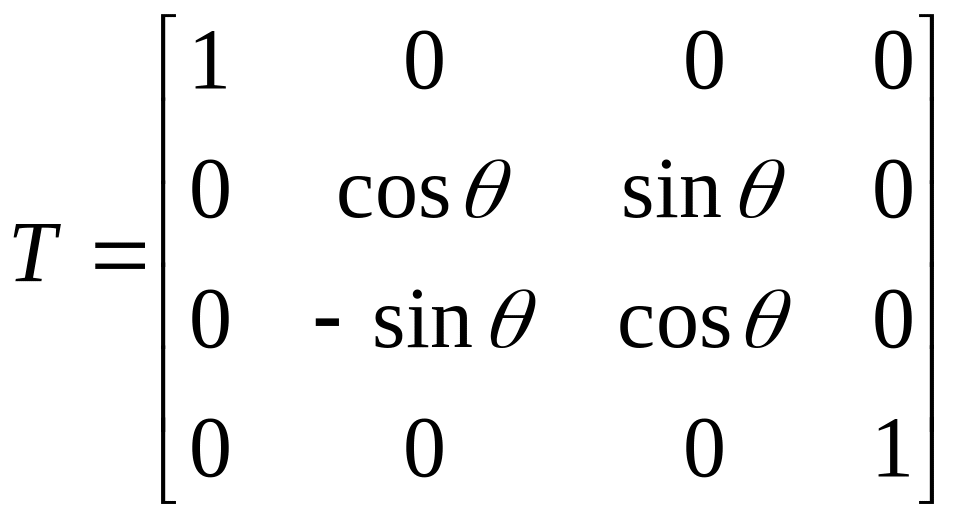
ри
вращении вокруг оси х размеры вдоль оси
х не изменяются. Таким образом, матрица
преобразований будет иметь нули в первой
строке и первом столбце, за исключением
единицы на главной диагонали. Это
приводит к матрице преобразования,
соответствующей повороту на угол q
вокруг оси х и определяемой соотношением
Вращение предполагается положительным, т. е. по часовой стрелке, если смотреть из начала координат вдоль оси вращения. Подобным образом вращение вокруг осей y и z определяется отношениями:
,
.
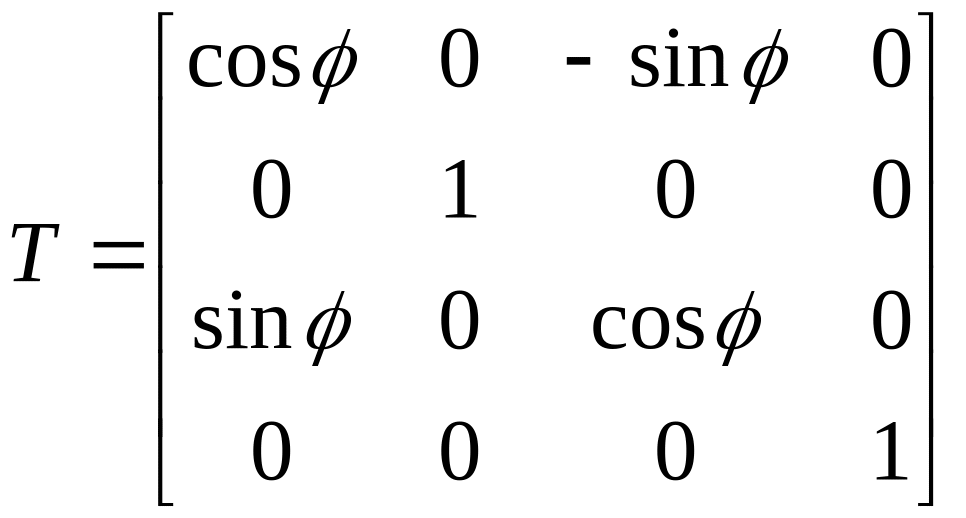Так как вращения описываются умножением матриц, то трехмерные вращения некоммутативные, т. е. порядок умножения будет влиять на конечный результат.
Идея описания точки вектором возникла из геометрических представлений. Теоремы геометрии развивались как для перспективной, так и для аффинной геометрии. В ней важными являются понятие параллельности и соотношения между параллельными линиями. Аффинное преобразование является комбинацией линейных преобразований, сопровождаемых переносом изображений. Для аффинного преобразования последний столбец в обобщенной матрице преобразования размера 4х4 должен быть равен [0 0 0 1]. Аффинные преобразования формируют удобную подсистему билинейных преобразований, так как произведение двух аффинных преобразований также является аффинным. Это позволяет представить обобщенную ориентацию системы точек по отношению к произвольной координатной системе при сохранении единичного значения однородной координаты H.
Матрица композиции нескольких преобразований может быть получена путем перемножения матриц, соответствующих этим преобразованиям, справа налево.
Концептуальная схема видового процесса в 3D графике. Типы плоских проекций.
И камера, и объект имеют свою собственную систему координат. Модель процесса визуализации выглядит примерно следующим образом:
(координаты в глобальных x, y, z) -> проекционное преобразование -> видовое преобразование -> отсечение -> проецирование и отображение на экранную поверхность -> координаты пикселя (x’, y’).
- Проекционное преобразование. Несоответствие между 3D объектами реального мира и 2D дисплеями разрешается введением проекции. Проецирование в общем случае - отображение точек, заданных в системе координат размерностью N, в точки в системе с меньшей размерностью. При отображении трехмерных изображений на дисплей три измерения отображаются в два. Проецирование выполняется с помощью прямолинейных проекторов (проецирующих лучей), идущих из центра проекции через каждую точку объекта до пересечения с картинной поверхностью (поверхностью проекции). Далее рассматриваются только плоские проекции, при которых поверхность проекции - плоскость в трехмерном пространстве. По расположению центра проекции относительно плоскости проекции различаются центральная и параллельные проекции.
- Видовое преобразование. Задав тип проекции, необходимо определить условия, при которых мы хотим видеть объект или сцену реального мира. Иными словами, задав сцену в мировых координатах, необходимо определить позицию глаза наблюдателя и место видовой плоскости - поверхности, на которой в конечном итоге появляется изображение. Меняя какие-то параметры, мы можем обеспечить любое желаемое визуальное представление сцены, включая визуализацию "изнутри".
- Отсечение. Мы можем визуализировать только некоторую часть 3D мира, следовательно необходимо определить 3D oкно и отсечь все, что не попадает в него. Это "окно"
называется "объем видимости". Этот процесс значительно более сложен, чем в 2D случае.
- проецирование и отображение на экранную поверхность. Финальные шаги - проецирование видового объема на видовую плоскость и преобразование (отображение) полученного окна в окно вывода дисплея.