Методы закраски полигональных поверхностей. Метод Гуро.

Существует три основных способа закраски многоугольников: однотонная закраска, закраска с интерполяцией интенсивности и закраска с интерполяцией векторов нормали.

При однотонной закраске предполагается, что и источник света и наблюдатель находятся в бесконечности, поэтому произведения L·N и R·V постоянны. На изображении могут быть хорошо заметны резкие перепады интенсивности между различно закрашенными многоугольниками. Если многоугольники представляют собой результат аппроксимации криволинейной поверхности, то изображение недостаточно реалистично.

В методе закраски с интерполяцией интенсивности (метод Гуро) нормали в вершинах многоугольников вычисляются как результат усреднения нормалей ко всем полигональным граням, которым принадлежит данная вершина. Используя значения нормалей, вычисляют интенсивности в вершинах по той или иной модели освещения. Эти значения затем используются для билинейной интерполяции: для данной строки сканирования вначале находят значения интенсивностей на ребрах, а затем линейно интерполируют между ними при закраске вдоль строки. Закраска Гуро лучше всего выглядит в сочетании с простой моделью с диффузным отражением, так как форма бликов при зеркальном отражении сильно зависит от выбора многоугольников, представляющих объект или поверхность.

Методы закраски полигональных поверхностей. Метод Фонга.

В методе закраски с интерполяцией нормали (метод Фонга) значение нормали вдоль строки интерполируется между значениями нормалей на ребрах для данной строки. Значения нормалей на ребрах получается как результат интерполирования между вершинами. Значения же нормалей в вершинах являются результатом усреднения, как и выше рассмотренном методе. Значение нормали для каждого из пикселов строки используется для вычислений по той или иной модели освещения.

Способы создания фотореалистических изображений

Глобальная модель освещения с трассировкой лучей. Отражение и преломление света. Прозрачность.

В основных моделях освещения и алгоритмах удаления невидимых линий и поверхностей рассматриваются только непрозрачные поверхности и объекты. Однако существуют и прозрачные объекты, пропускающие свет, например, такие, как стакан, ваза, окно автомобиля, вода. При переходе из одной среды в другую, например из воздуха в воду, световой луч преломляется; поэтому торчащая из воды палка кажется согнутой. Преломление рассчитывается по закону Снеллиуса, который утверждает, что падающий и преломляющий лучи лежат в одной плоскости, а углы падения и преломления связаны формулой h₁sinq = h₂sinq ', где h₁ и h₂ — показатели преломления двух сред, q — угол падения, q ' — угол преломления. Ни одно вещество не пропускает весь падающий свет, часть его всегда отражается.

Т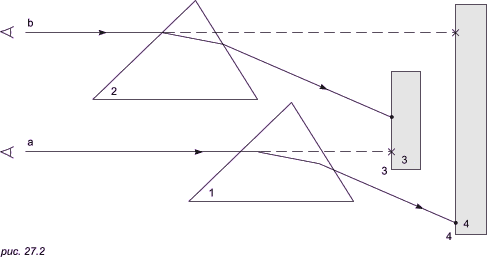 ак же, как и отражение, пропускание может быть зеркальным (направленным) или диффузным. Направленное пропускание свойственно прозрачным веществам, например стеклу. Если смотреть на объект сквозь такое вещество, то, за исключением контурных линий криволинейных поверхностей, искажения происходить не будет. Если свет при пропускании через вещество рассеивается, то мы имеем диффузное пропускание. Такие вещества кажутся полупрозрачными или матовыми. Если смотреть на объект сквозь такое вещество, то он будет выглядеть нечетким или искаженным.На рис. 27.2 показаны некоторые практические следствия преломления.

П оказатель преломления объектов 1 и 2 одинаков и больше, чем у окружающей среды. Объекты 3 и 4 непрозрачны. Если не принимать во внимание преломление, то луч a пересечется с объектом 3 (пунктирная линия). Однако из-за преломления он отклоняется и пересекается с объектом 4, то есть объект 4 можно увидеть, только учитывая эффект преломления. Если же рассматривать луч b, то без учета преломления он пересекается с объектом 4, хотя на самом деле он пересекается с объектом 3, то есть здесь объект, который видим, на самом деле увидеть нельзя. Все это необходимо иметь в виду при создании реалистических изображений. Нечто похожее происходит при встраивании перспективного преобразования в видовое преобразование. Обычно перспективное преобразование проводится для того, чтобы получить искаженный объект, который затем строится в аксонометрической проекции с точкой наблюдения, удаленной в бесконечность (рис. 27.3).

На рис. 27.3a луч, исходящий из точки P, пересекает неискаженный объект в точке i и после преломления попадает в точку b плоскости фона. На рис. 27.3b показан объект после перспективного преобразования. Теперь луч пересекает объект в преобразованной точке i', преломленный луч пересекается с фоном в точке b' с противоположной стороны от центральной линии. Это происходит из-за неправильных угловых соотношений между искаженным (преобразованным) объектом и искаженным (преломленным) лучом. На первый взгляд для получения верного результата достаточно знать истинные угловые соотношения в точках пересечения луча с объектом. Однако это не так, потому что длина пути луча в преобразованном объекте также меняется. Разница в длине пути приводит к тому, что, во-первых, не совпадают точки выхода луча из объекта, так что луч все равно не попадает в правильную точку фона. Во-вторых, меняется количество поглощенного объектом света, поэтому исходящий луч имеет другую интенсивность. Для того чтобы устранить влияние преломления, можно либо применять алгоритмы, работающие в пространстве объекта, либо пользоваться специальными преобразованиями между пространствами объекта и изображения. Однако проще включить преломление в алгоритмы построения видимых поверхностей методом трассировки лучей, использующие глобальную модель освещения. В простейших реализациях эффекты прозрачности преломления вообще не рассматриваются, и явления, показанные на рис. 27.2 и рис. 27.3, не учитываются. Кроме того, не принимается во внимание, как путь, пройденный лучом в среде, влияет на его интенсивность. Самые ранние разработки в этой области принадлежат Ньюэлу. Простое пропускание света можно встроить в любой алгоритм удаления невидимых поверхностей, кроме алгоритма с z-буфером. Прозрачные многоугольники или поверхности помечаются, и если видимая грань прозрачна, то в буфер кадра записывается линейная комбинация двух ближайших поверхностей. При этом интенсивность I = tI₁ + (1 - t)I₂, 0 <= t <= 1, где I₁ — видимая поверхность, I₂ — поверхность, расположенная непосредственно за ней, t — коэффициент прозрачности I₁. Если поверхность совершенно прозрачна, то t = 0, а если непрозрачна, то t = 1. Если I₂ тоже прозрачна, то алгоритм применяется рекуррентно, пока не встретится непрозрачная поверхность или фон. Если многоугольники записываются в буфер кадра в соответствии с приоритетами глубины, как в алгоритме Ньюэла-Ньюэла-Санча, тогда I₂ будет соответствовать значению, записанному в буфер кадра, а I₁ — текущей поверхности. Для криволинейных поверхностей, например, таких, как ваза или бутылка, линейной аппроксимации недостаточно, так как вблизи контурных линий прозрачность уменьшается из-за толщины материала. Чтобы точнее изобразить это явление, Кэй предложил несложную нелинейную аппроксимацию на основе z-составляющей нормали к поверхности. В частности, коэффициент прозрачности: t = t_min + (t_mах - t_min)[1 -(1 - |n_z|)^p], где t_min и t_max — минимальная и максимальная прозрачность объекта, n_z есть z-составляющая единичной нормали к поверхности, р — коэффициент степени прозрачности, t — прозрачность пиксела или точки объекта.