14.Характеристика відносних показників планового завдання, виконання плану та порівняння.
Відносна величина планового завдання – це відношення величини показника плану (yПЛ) до взятої за базову фактичної величини плану за попередній період (yП).
VПЗ = yПЛ / yП (100 %)
Відносна величина виконання плану (VВП) – це відношення фактично досягнутої величини (yФАКТ) до планового базового завдання (yПЛ) на досліджуваний період часу.
VВП = yФАКТ / yПЛ (100 %)
Відносна величина порівняння служить для співставлення однойменних абсолютних величин, що відносяться до різних сукупностей.
VПОР = a1 / a2 (100 %)
15.Характеристика відносних показників інтенсивності та диференціації.
Відносна величина інтенсивності – це відношення між різнойменними абсолютними величинами, що характеризують ознаки однієї сукупності або ознаки певним чином пов’язаних між собою різних сукупностей.
VІНТ = a0 / a (100 %).
VІНТ = розмір досліджуваного явища / обсяг середовища, в якому воно розвивається.
Відносна величина диференціації характеризує результат порівняння для даної сукупності двох відносних величин за чисельністю (v1) і величиною будь-якої іншої ознаки (v2).
VДИФ = v1 / v2 (100 %)
16.Суть і призначення середніх величин в статистиці. Класифікація середніх величин. Середня арифметична величина та її властивості.
Роль середніх величин як узагальнюючих показників, що характеризують статистичні сукупності, надзвичайно важлива. Не можна зрозуміти сутності соціально-економічних явищ без використання середніх величин. Усередненню підлягають продуктивність праці, ціна, собівартість одиниці продукції, дохідність, рентабельність, урожайність с/г культури, продуктивність худоби та птиці, споживання продовольчих товарів на душу населення та багато інших показників.
Середня величина – це узагальнена характеристика множини індивідуальних значень деякої кількісної ознаки.
Види середніх величин:
1.Середня арифметична.
2.Середня гармонійна.
3.Середня квадратична.
4.Середня геометрична.
5.Середня хронологічна.
6.Середня прогресивна.
7.Структурні середні:
7.1.Мода.
7.2.Медіана.
Середня арифметична величина:
(проста)
(зважена)
Властивості середньої арифметичної:
1.Сума відхилень окремих значень ознаки від середнього значення ознаки = 0.
+x1
-
+x2 -
+ …
xn -
-------------
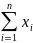- n
=
–
n
=
0
2.При збільшенні або зменшенні кожної варіанти на сталу величину а середнє зміниться на цю ж величину.
=
=
=
a =
a
3.При збільшенні або зменшенні кожної варіанти в а разів середнє зміниться у стільки ж.
=
= a
4.Якщо частоти змінити в однакову кількість разів, то середнє не зміниться.
=
17.Суть і призначення середніх величин в статистиці. Середня гармонічна та середня квадратична величина.
Роль середніх величин як узагальнюючих показників, що характеризують статистичні сукупності, надзвичайно важлива. Не можна зрозуміти сутності соціально-економічних явищ без використання середніх величин. Усередненню підлягають продуктивність праці, ціна, собівартість одиниці продукції, дохідність, рентабельність, урожайність с/г культури, продуктивність худоби та птиці, споживання продовольчих товарів на душу населення та багато інших показників.
Середня величина – це узагальнена характеристика множини індивідуальних значень деякої кількісної ознаки.
Середня гармонійна величина – це величина, обернена до середньої арифметичної, обчисленої з оберненим значенням ознаки.
г
=
(проста)
г
=
(зважена)
ai – вага оберненої величини 1/xi
Середня квадратична величина застосовується, якщо досліджується варіація ознаки.
=
(проста)
=
(зважена)