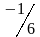Үйлесiмсiз

группой совместных событий

Үйлесiмдi оқиғалардың тобы

произведением событий

оқиғалардың көбейтіндісі

суммой событий

оқиғалардың қосындысы

.случаев события А к числу возможных исходов событий называется

А оқиғасына қолайлы оқиғалар санының барлық мүмкiн оқиғалар санының катынасы дегенiмiз:

вероятностью события А

А оқиғасының ықтималдығы

условной вероятностью события А

À оқиғасының шартты ықтималдығы

относительной частотой события А

À оқиғасының салыстырмалы жиілігі

частотой события А

Аоқиғасының жиілігі

статистической вероятностью события А

А оқиғасының статистикалық ықтималдығы

. Отношение числа испытаний, в которых произошло событие, к общему числу проведенных испытаний называется

Оқиға болғандағы, өткiзiлген сынаулардың сынаулардың жалпы санының қатынасы дегенiмiз:

относительной частотой событий А

А оқиғасының салыстырмалы жиілігі

Относительная частота 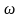изменяется

салыстырмалы жиілігі өзгередi

0,1

Событие, состоящее в появлении А или В, или обоих этих событий, называется

А және В оқиғаларының, немесе екеуiнiң бiрдей пайда болуының оқиғасы:

суммой двух событий А и В

Ажәне В оқиғаларының қосындысы

. Два события, образующих полную группу, называются

Екi оқиғадан толық топ құралса, олар –––– болып табылады

Противоположными

қарама-қарсы

Событие, состоящее в том, что имеют место оба события А и В, называется

А және В оқиғалардың бiрге пайда болуы, А және В оқиғалардың –––––––деп аталады.

Произведение

көбейтiндiсi

. Чья эта формула:

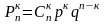
Формуланың аталуы

Бернулли

. -нің қандай мәнінде қандай төмендегі екі жазықтықтың біріне-бірі перпендикуляр болады:

Определить, при каком значении следуюшие пары уравнений будуть определить перпендикулярные плоскости:

6

. -нің қандай мәнінде төмендегі екі жазықтықтың біріне-бірі перпендикуляр болады: Определить, при каком значении следуюшие пары уравнений будуть определить перпендикулярные плоскости:

-19

. -нің қандай мәнінде төмендегі екі жазықтық біріне-бірі перпендикуляр болады: 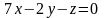және

Определить, при каком значении следуюшие пары уравнений будуть определить перпендикулярные плоскости:

и .

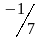
. -нің қандай мәнінде төмендегі екі жазықтықтың біріне-бірі перпендикуляр болады: 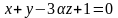және

Определить, при каком значении следуюшие пары уравнений будуть определить перпендикулярные плоскости:

и .