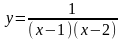- •Оң жағындағы бос мүшенiң барлығы нольге тең
- •Функцияныє үзiлiс нѕктелерiн тап
- •Функцияның үзiлiс нүктелерiн тап
- •Функцияның үзiлiс нүктелерiн тап
- •Функцияның интегралы
- •Функцияныє алғашқы бейнесi
- •Бiртектi теңдеудiң жалпы шешiмiмен бiртексiз дифференциял теңдеудiң дербес шешiмiнiң қосындысы.
- •Егер сипаттамалық теңдеудiң түбiрi комплекстi
- •Үйлесiмсiз
- •Үйлесiмдi оқиғалардың тобы
- •А оқиғасының ықтималдығы
Математика
1 499 40
Если
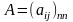 квадратная матрица, то главную диагональ
образуют элементы
квадратная матрица, то главную диагональ
образуют элементы
Егер квадратты матрица болса,онда басты диагоналдың элементтерiн жаз
а11, а22, …, аnn
.Если квадратная матрица, то побочную диагональ образуют элементы
Егор квадратты матрица болса, онда көмекші диагоналдың элементтерiн жаз
а1n, а2n-1, …, аn1
.Определитель
матрицы К=
Матрицаның анықтауышы
det K= 10
.Определитель
матрицы К=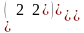
Матрицаның анықтауышы
det K= 14
.Является ли данная система совместной
Берiлген теңдеу жүйесi үйлесiмдi ме
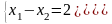
үйлесiмдi - совместна
.Является ли данная система совместной
Берiлген теңдеу жүйесi үйлесiмдi ме

үйлесiмсiз – не совместна
.Является ли данная система совместной
Берiлген теңдеу жүйесi үйлесiмдi ме
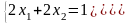
үйлесiмсiз – не совместна
.Является ли данная система совместной
Берiлген теңдеу жүйесi үйлесiмдi ме
үйлесiмдi - совместна
.Если матрица А5х4, то из перечисленных матриц 1. В5х3 2. С4х5 3. D4x3 4. K3x5 5. M4x1 6. N4x5 транспонированными к А могут являться
Егер А5х4 болса, берiлген матрицалардың қайсысы А матрицаның транспонирленген матрицасы болады
2;6
.Если матрица А3х4, то из перечисленных матриц 1. В5х3 2. С4х5 3. D4x3 4. K3x5 5. M4x3 6. N4x5 транспонированными к А могут являться
Егер А3х4 болса, берiлген матрицалардың қайсысы А матрицаның транспонирленген матрицасы болады
3;5
.Если матрица А3х5, то из перечисленных матриц 1. В5х3 2. С4х5 3. D5x3 4. K3x5 5. M4x3 6. N4x5 транспонированными к А могут являться
Егер А3х5 болса, берiлген матрицалардың қайсысы А матрицаның транспонирленген матрицасы болады
1;3
.Если матрица А3х2, то из перечисленных матриц 1. В2х3 2. С6х4 3. D4x3 4. K3x5 5. M2x3 6. N6x4 транспонированными к А могут являться
Егер А3х2 болса, берiлген матрицалардың қайсысы А матрицаның транспонирленген матрицасы болады
1;5
.Матрица А имеет порядок m x n, а В – k x d. Чтобы их перемножить, необходимо чтобы
А матрицасының ретi m x n,ал В – k x d.
Осы екi матрицаны көбейту үшiн қайсы шарт керек
n=k
.Матрица А имеет порядок m x с, а В – k x d. Чтобы их перемножить, необходимо чтобы
А матрицасының ретi m x с,ал В – k x d.
Осы екi матрицаны көбейту үшiн қайсы шарт керек
с=k
.Если
К=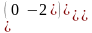
 ,
то N=
,
то N= К
равна
К
равна
Егер К= , N= К неге тең
N=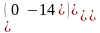
.Если
К=
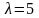 ,
то N=
К
равна
,
то N=
К
равна
Егер К= , онда N= К тең
N=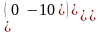
.Если в квадратной матрице все ее элементы, стоящие ниже или выше ее главной диагонали равны нулю, то эта матрица называется
Егер квадраттық матрицаның бас диогоналының астыңғы жағы және жоғарғы жағы нөлге тең болса ол қандай матрица
Треугольной
Үшбұрышты
.Если в квадратной матрице все ее элементы равны нулю, то эта матрица называется
Егер квдратты матрицаның барлық элементтерi нөлге тең болса,онда матрица
Нулевой
Нөлдiк
.Если все недиагональные элементы квадратной матрицы равны нулю, то матрица называется
Егер диогоналдан басқа элементтерi нөлге тең болса,онда матрица
Диагональной
Диогоналдық
.Если у диагональной матрицы все диагональные элементы равны единице, то матрица называется
Егер диогоналдық матрицаның барлық элементтерi бiрге тең болса ,онда матрица
Единичной
Бiрлiк
.Определитель
матрицы М=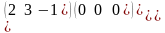 равен
равен
М= матрицасыныє анықтауышын тап
det М=0
.Матрица
К=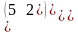 ,
обратная ей
,
обратная ей
К= ,керi матрицасын тап
К-1=
.Матрица
К=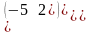 ,
обратная ей
,
обратная ей
К= ,Матрицасының керi матрицасын тап
К-1=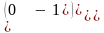
.Матрица К= , транспонированной к ней будет матрица
К= ,матрицасының транспонирленген матрицасын жаз
КТ=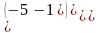
.Определитель матрицы равен
матрицасының анықтауышын тап
2
.Определитель
матрицы
 равен
равен
матрицасыныє анықтауышын тап
–4
.Определитель
матрицы
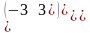 равен
равен
матрицасының анықтауышын тап
0
.Определитель
матрицы
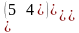 равен
равен
матрицасының анықтауышын тап
6
.Система уравнений, у которой не существует решения, называется
Теңдеулер жүйесiнiң шешiмi жоқ болса,қалай аталады
Несовместной
үйлесiмсiз
.Система уравнений, у которой существует множество решений, называется
Теңдеулер жүйесiнiң шешiмi көп болса,онда қалай аталады
Неопределенной
Анықталмаған
.Система уравнений, у которой существует единственное решение, называется
Теңдеулер жүйесiнiң жалғыз шешiмi болса,қалай аталады
Определенной
Анықталған
.Система m линейных уравнений с n переменными называется системой линейных однородных уравнений, если
n айнымалысы бар m теңдеуден тұратын теңдеулер жүйесi бiртектi деп аталады, егер
Все их свободные члены равны нулю
Оң жағындағы бос мүшенiң барлығы нольге тең
.Система m линейных уравнений с n переменными называется системой линейных неоднородных уравнений, если
n айнымалысы бар m теңдеуден тұратын теңдеулер жүйесi бiртектi емес, егер
Хотя бы один из свободных членов не равен нулю
Оң жағындағы бос мүшенiң ең болмағанда бiреуi ноль емес
.Если в системе уравнений
Егер теңдеулер жүйесi мына түрде берiлсе ,қалай аталады
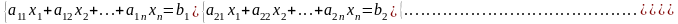 b1
=b2
=…=bm=0,
то система называется
b1
=b2
=…=bm=0,
то система называется
Однородной
Бiртектi
.В
матрице А=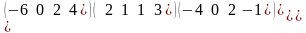 побочную
диагональ составляют элементы
побочную
диагональ составляют элементы
А= Матрицасының көмекшi диогоналының элементтерiн жаз
4,1,0,7
.В
матрице А=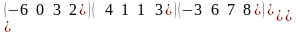 главную
диагональ составляют элементы
главную
диагональ составляют элементы
А= Басты диогоналының элементтерiн жаз
–6,1,7,3
.В
матрице А=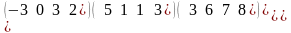 побочную
диагональ составляют элементы
побочную
диагональ составляют элементы
А= Матрицасының көмекшi диогоналының элементтерiн жаз
2,1,6,10
.В матрице А= главную диагональ составляют элементы
А= Басты диогоналының элементтерiн жаз
–3,1,7,3
.Найти
алгебраическое дополнение А11
матрицы
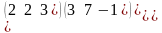
Матрицаның А11 алгебралық толықтауышын есепте
30
.Найти алгебраическое дополнение А12 матрицы
Матрицаның А12 алгебралық толықтауышын есепте
-12
.Найти алгебраическое дополнение А13 матрицы
Матрицаның А13алгебралық толықтауышын есепте
6
.Найти алгебраическое дополнение А21 матрицы
Матрицаның А21 алгебралық толықтауышын есепте
–2
.Найти алгебраическое дополнение А22 матрицы
Матрицаның А22 алгебралық толықтауышын есепте
8
.Найти алгебраическое дополнение А23 матрицы
Матрицаның А23 алгебралық толықтауышын есепте
–4
.Найти алгебраическое дополнение А31 матрицы
Матрицаның А31 алгебралық толықтауышын есепте
–23
.Найти алгебраическое дополнение А32 матрицы
Матрицаның А32 алгебралық толықтауышын есепте
11
.Найти алгебраическое дополнение А33 матрицы
Матрицаның А33 алгебралық толықтауышын есепте
8
.Найти минор М11 матрицы
Матрицаның М11 минорын тап
30
.Найти минор М12 матрицы
Матрицаның М12 минорын тап
12
.Найти минор М13 матрицы
Матрицаның М13минорын тап
6
.Найти минор М21 матрицы
Матрицаның М21 минорын тап
2
.Найти минор М22 матрицы
Матрицаның М22 минорын тап
8
.Найти минор М23 матрицы
Матрицаның М23 минорын тап
4
.Найти минор М31 матрицы
Матрицаның М31минорын тап
–23
.Найти минор М32 матрицы
Матрицаның М32 минорын тап
-11
.Найти минор М33 матрицы
Матрицаның М33 минорын тап
8
.При умножении всех элементов некоторой строки матрицы на число определитель исходной матрицы
Матрицаның кез-келген қатарыныє элементтерiн санға көбейтсек матрица анықтауышы
Умножается на это число
Осы санға көбейтiледi
.Если две строки матрицы равны, то ее определитель
Матрицаныє екi қатары нөлге тең болса,онда анықтауыш неге тең
det =0
.Если какая-либо строка (столбец) матрицы состоит из одних нулей,
то ее определитель
Егер матрицаныє қандайда бiр қатары жґне тiк жолы нөлден тұратын болса,матрицаның анаықтауышы
det =0
.При транспонировании матрицы ее определитель
Тронспонирленген матрицаның анықтауышы
Не изменяется
Өзгермейдi
.При перестановке двух строк (столбцов) матрицы ее определитель
Матрицаның қатарын және тiк жолын ауыстырғанда матрицаның анықтауышы
Меняет знак на противоположный
Таңбасы керi таєбаға ауысады
.Если квадратная матрица содержит две одинаковые строки (столбца),
то ее определитель
Егер квадратты матрица екi бiрдей қатардан жґне тiкжолдан тұрса,онда матрицаның анықтауышы
det =0
.Если элементы двух строк (столбцов) матрицы пропорциональны, то
ее определитель
Егер матрицаның екi қатары жґне тiк жолы пропорциональ болса,онда анықтауышы
det =0
.Размер матрицы С=А1х2В2х3 равен
С=А1х2В2х3 Матрицаның өлшемi неге тең
С1х3
матрицы С=А2х2В2х3 равен
С=А2х2В2х3 Матрицаның өлшемi неге тең
С2х3
.Размер матрицы С=А5х2В2х4 равен
С=А5х2В2х4 Матрицаның өлшемi неге тең
С5х4
.Размер матрицы С=А2х1В2х3 равен
С=А2х1В2х3 Матрицаның өлшемi неге тең
Нет правильного ответа
Дұрыс жауабы жоқ
.Размер матрицы С=А4х2В3х4 равен:
С=А4х2В3х4 матрицаның өлшемi неге тең:
Нет правильного ответа
Дұрыс жауабы жоқ
.Даны
матрицы А=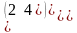 и В=
и В=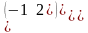 их сумма равна
их сумма равна
Берiлген А= жґне В= матрицасының қосындысы тең

.Даны матрицы А= и В= их разность равна
Берiлген А= жґне В= матрицасының айырмасы тең
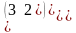
.Даны матрицы А= и В= их произведение равно
Берiлген А= жґне В= матрицасының көбейтiндiсi тең
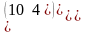
.Даны
матрицы А=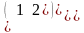 и В=
их
сумма равна
и В=
их
сумма равна
Берiлген А= жґне В= матрицасының қосындысы тең
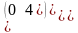
.Даны матрицы А= и В= их разность равна
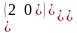
.Даны матрицы А= и В= их произведение равно
Берiлген А= жґне В= матрицасының көбейтiндiсi тең

.Дана матрица А= , то А2 равна
Берiлген А= ,матрицасының квадраты А2 тең
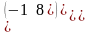
.Дана матрица В= , то В2 равна
Берiлген В= ,матрицасының квадраты В2тең
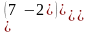
.Даны
матрицы А=
и В=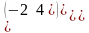 их
произведение равно
их
произведение равно
Берiлген А= жґне В= матрицасының көбейтiндiсi тең
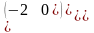
.Дана матрица А= , то А2 равна
Берiлген А= ,матрицасының А2 квадраты тең

.Дана матрица В= , то В2 равна
Берiлген В= ,матрицасының В2 квадраты тең
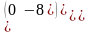
.Даны
матрицы А=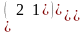 и В=
и В= их
произведение равна
их
произведение равна
Берiлген А= жґне В= матрицаларының көбейтiндiсi теє

.Даны матрицы А= и В= их сумма равна
Берiлген А= жґне В= матрицаларының көбейтiндiсi
.Даны матрицы А= и В= их разность равна
Берiлген А= жґне В= матрицаларының айырмасы тең
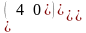
.Дана матрица В= , то В2 равна
В= ,берiлген,онда В2 тең

.Определитель
матрицы К=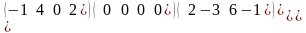 равен
равен
Матрицаныє анықтауышы тең
det K=0
.Определитель
матрицы К=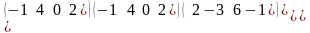 равен
равен
Матрицаның анықтауышы тең
det K=0
.Определитель
матрицы К=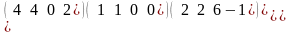 равен
равен
Матрицаның анықтауышы тең
det K=0
.Матрица А-1 называется обратной для матрицы А (квадратная порядка n), если выполняется условие
АА-1= А-1А= Е
.Размер матрицы К=М2х4В4х2 равен
Матрицаның К=М2х4В4х2 өлшемi неге тең
К2х2
.Размер матрицы К=М3х4В4х2 равен
Матрицаның К=М3х4В4х2 өлшемi неге тең
К3х2
.Размер матрицы К=М2х1В1х3 равен
Матрицаның К=М2х1В1х3 өлшемi неге тең
К2х3
.Размер матрицы К=М5х4В4х1 равен
Матрицаның К=М5х4В4х1 өлшемi неге тең
К5х1
.Найти
алгебраическое дополнение А12
матрицы

матрицасының А12 алгебралық толықтауышын тап
1
.Совокупность m x n действительных чисел, расположенных в виде прямоугольной таблицы, где m – число строк, n – число столбцов таблицы называется
m қатардан n бағанадан туратын m x n сандардын кесте түрiнде жазылуы
Прямоугольной матрицей
Тiк бұрышты
.Если матрица А= , то транспонированная к ней матрица АТ
Транспонирленген матрицаны тап
АТ=
.Если в матрице число строк равно числу ее столбцов, то такая матрица называется
Егер матрицаның тiк жолы мен жатық жолы тең болса матрица қалай аталады
Квадратной
Квадратты
.Если в системе уравнений хотя бы одно из чисел b1 , b2 ,…,bm не равно нулю, то система называется
Егер теңдеулер жүйесiнiң
b1 , b2 ,…,bm бiреуi нөлге тең болмаса қалай аталады
Неоднородной
Бiртексiз
.Если
А=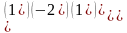 ,
В=
,
В= ,
то АВ равно
,
то АВ равно
Егер А= , В= , онда АВ тең
АВ=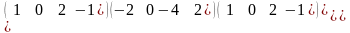
.Вычислить
определитель матрицы М=
Матрицасыныє анықтауышын есепте
–2
.Вычислить
определитель матрицы М=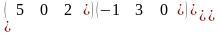
Матрицасыныє анықтауышын есепте
7
.Вычислить
определитель матрицы М=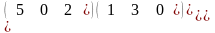
Матрицасының анықтауышын есепте
11
.Формулы Крамера имеют вид
Крамер формуласын көрсет
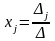
.Метод решения системы путем последовательного исключения переменных называется методом
Диогоналдан басқа элементтерiн нөлге айналдырып теңдеулер жүйесiн шешу әдiсi
Гаусса
Гаусс
.Решить
систему уравнений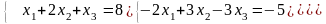
Теңдеу жүйесiн шеш
1;2;3
.Векторы
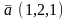 и
и
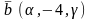 будут параллельны, если
будут параллельны, если
жґне векторлары параллель болады, егер
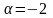 ;
;
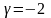
.Даны
векторы
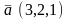 и
и
 .
Длина вектора
.
Длина вектора
 равна
равна
Берiлген
вектор
жґне
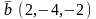 .вектордың
ұзындығы
тең
.вектордың
ұзындығы
тең
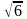
.Даны
векторы
и
.
Длина вектора
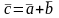 равна
равна
Берiлген вектор жґне. вектордың ұзындығы тең
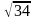
.Даны векторы и . Координаты вектора равны
Берiлген вектор и . вектордың кординатасы неге тең
(5,3,0)
.Даны
векторы
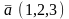 и
и
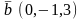 .
Координаты вектора
равны
.
Координаты вектора
равны
Берiлген вектор жґне . вектордың кординатасы неге теє
(1,3,0)
.Даны
векторы
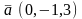 и
и
 .
Координаты вектора
равны
.
Координаты вектора
равны
Берiлген вектор жґне . вектордың кординатасы неге теє
(4,7,-2)
.Уравнение прямой, проходящей через точку (-2,0) перпендикулярно
прямой 3х+у+4=0, имеет вид
3х+у+4=0 тѕзуге перпендикуляр болып (-2,0) нѕкте арқылы өтетiн
түзудiң теңдеуiн көрсет
у=х/3+2/3
.Даны
векторы
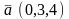 и
и
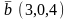 .
Косинус угла между ними равен
.
Косинус угла между ними равен
Векторлардың арасындағы бұрыштың косинусын тап
16/25
.Даны
векторы
 и
и
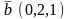 .
Длина вектора
равна
.
Длина вектора
равна
Векторлардың ұзындыңы тең
3
.Даны
векторы
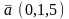 и
.
Координаты вектора
равны
и
.
Координаты вектора
равны
Векторлардың ұзындықтарының координатасы
(0,0,8)
 и
и
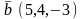 .Скалярное
произведение
.Скалярное
произведение
 равно
равно
Векторлардың скаляр көбейтiндiсi тең
-3
.Из перечисленных прямых: 1) у=4х+1; 2) у=2х-3; 3) у=-х/2+4;
4) у=-4х-5, перпендикулярными являются
Берiлген түзулердiң қайсылары перпендикуляр
2,3
.Дан
вектор
 {1,-1,0}.
Его длина равна
{1,-1,0}.
Его длина равна
Векторлардың ұзындығы
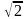
.Из перечисленных уравнений прямых: 1) 3х-4у+5=0; 2) 2х+5у-4=0;
3) 6х-8у-3=0; 4) у=3х/4+2; 5) 3х-5у+5=0, параллельными являются
Берiлген түзулердiң қайсылары паралель
1,3,4
.Даны
векторы
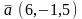 и
и
 .Скалярное
произведение
равно
.Скалярное
произведение
равно
Скаляр көбейтiндiсi тең
–19
.Даны
векторы
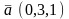 и
.
Косинус угла между ними равен
и
.
Косинус угла между ними равен
Векторлардың арасындағы бұрыш тең
4/5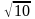
.Даны
векторы
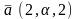 и
.
Эти векторы будут
и
.
Эти векторы будут
перпендикулярны, если
Берiлген векторлар перпендикуляр болады егер

.Даны
векторы
 и
и
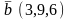 .
Эти векторы будут параллельны,
.
Эти векторы будут параллельны,
если
Берiлген векторлар паралель болады,егер

.Даны
векторы
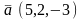 и
.
Координаты вектора
равны
и
.
Координаты вектора
равны
Векторлардың ұзындықтарының кординатасы тең
(5,1,0)
.Уравнение прямой, проходящей через точки с координатами
(2,3) и (-1,0) имеет вид
(2,3) жґне (-1,0) Нүктелерi арқылы өтетiн түзудiң теңдеуi
у=х+1
.Условие параллельности прямых записывается в виде
Түзулердiң паралелдiк шарты қай түрде жазылады
k1=k2
.Условие перпендикулярности прямых записывается в виде
Түзулердiң перпендикулярлық шарты қай түрде жазылады
k1k2=-1
.Бұрыштық коэффициент арқылы
берiлген және ордината осьiн қиятын теңдеу қайсы?
Каков вил уравнения прямой с данным угловым коэффициентом и отсекающей на оси ординат данный отрезок?
y=kx +b
.Бұрыштық коэффициент арқылы
берiлген және жазықтықта берiлген нүкте М(х0,у0) арөылы өтетiн түзудiң теңдеуi?
Каков вид уравнения прямой с данным угловым коэффициентом и проходящей через данную точку М(х0,у0) на плоскости?
y-y0=k(x-x0)
.Жазықтықта берiлген 2 нүкте
арқылы өтетiн түзудiң теңдеуi.
Каков вид уравнения прямой, проходящей через две данные точки на плоскости?
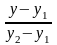 =
=
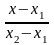
.Жазықтықтағы түзудiң жалпы
теңдеуi қайсы?
Каков вид общего уравнения прямой на плоскости?
Ax+By+C=0
.Жазықтықтағы түзудiң нормаль
теңдеуi қайсы?
Каков вид нормального уравнения прямой на плоскости?
xcos +ysin - p =0
.Кесiндiлiк түрде берiлген түзу
теңдеуi.
Каков вид уравнения прямой в отрезках на осях на плоскости?
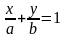
.Ордината осьiне параллель
болатын түзудiң теңдеуi.
Каков вид уравнения прямой, параллельной оси ординат на плоскости?
х=а
.Абсцисса осьiне параллель
болатын түзудiң теңдеуi.
Каков вид уравнения прямой, параллельной оси абсцисс на плоскости?
y =b
.Абсцисса осьiнiң теңдеуi қайсы?
Каков вид уравнения оси абсцисс?
y =0
.Ордината осьiнiң теңдеуi қайсы?
Каков вид уравнения оси ординат
x=0
.Числовым рядом называется
Сандық қатар қалай аталады
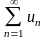
.Суммой числового ряда называется
қатарыныє қосындысы дегенiмiз
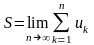
.n-ой частичной суммой числового ряда называется
сандық қатарының n бөлiгiнiң қосындысы дегенiмiз
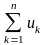
.Остатком числового ряда называется
сандық қатарының қалдық қатары дегенiмiз
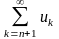
.Если
для числового ряда
:
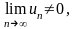 то ряд
то ряд
Егер сандық қатары ѕшiн болса, онда
расходится
жинақталмайды
.Необходимый признак сходимости числового ряда
сандық қатарының жинақталуының қажеттi шарты
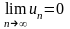
.Какой ряд называется гармоническим
Гармоникалық қатарды көрсет
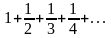
.Обобщенный
гармонический ряд
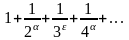 сходится при каких значениях
сходится при каких значениях

-ның қандай мәнiнде гармоникалық қатары жинақталады
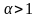
.Геометрический
ряд a+aq+aq2+aq3+…,
a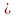 0
сходится, если
0
сходится, если
a+aq+aq2+aq3+…, a 0 геометриялық қатары жинақталады, егер

.Обобщенный гармонический ряд расходится при каких значениях
-ның қандай мґнiнде гармоникалық қатары жинақталады
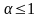
.Геометрический ряд a+aq+aq2+aq3+…, a 0 расходится, если
a+aq+aq2+aq3+…, a 0 геометриялық қатары жинақталады, егер
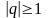
.С помощью какого признака доказывается, сходится или расходится обобщенный гармонический ряд
қандай белгiге байланысты гармоникалық қатардыє жинақталуы не жинақталмауы дәлелденедi
интегрального признака
интегралдық белгiге
.Сходимость числового ряда по признаку Даламбера: ряд сходится, если
сандық қатары Даламбер белгiсi бойынша жинақталады, егер
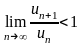
.Сходимость числового ряда по признаку Коши: ряд сходится, если
сандық қатары Коши белгiсi бойынша жинақталады, егер
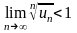
.Предельный
признак сравнения: если
и
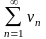 ряды
с положительными членами и существует
…, то ряды одновременно сходятся или
расходятся
ряды
с положительными членами и существует
…, то ряды одновременно сходятся или
расходятся
Шектiк салыстыру белгiсi егер жґне қатарлары оң мүшелi болып жґне … орындалса, онда қатарлар бiр уақытта жинақталады не жинақталмайды
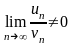
.По признаку Даламбера: ряд расходится, если
сандық қатары Даламбер белгiсi бойынша жинақталмайды, егер
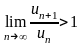
.По признаку Коши: ряд расходится, если
сандық қатары Коши белгiсi бойынша жинақталмайды, егер
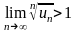
.Интегральный признак сходимости: для сходимости положительного и не возрастающего члена an=f(n) числового ряда необходимо и достаточно чтобы сходился несобственный интеграл …
Жинақталудыє интегалдық белгiсi оң мүшелi өспейтiн an=f(n) сандық қатары жинақталуы үшiн оның … меншiксiз интегралы жинақталуы қажеттi жґне жеткiлiктi
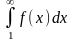
.Какой признак используется для исследования сходимости знакочередующегося ряда
Айнымалы таңбалы қатарыныє жинақталуы қандай белгi арқылы зерттеледi
признак Лейбница
Лейбниц белгiсi
.Какие условия (условие) проверяются при исследовании сходимости знакочередующегося ряда
Айнымалы таңбалы қатарлардың жинақталуын зерттеуде қандай шарттар тексерiледi
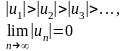
Чья
эта формула:

Формуланың аталуы
Байеса
Укажите формулу полной вероятности:
Толық ықтималдылықтың формуласын көрсет.
Р(А)=
Чему равна сумма вероятностей событий, образующих полную группу?
Толық топты құрайтын оқиғалардың ықтималдықтарының қосындысы неге тең?
1
Функцией распределения называется
Жiктеу функциясы дегенiмiз
F(x)=P(X<x)
Плотностью распределения вероятностей непрерывной СВ Х называется
Үзiлiссiз кездейсоқ Х шаманың тығыздықтық жiктеу ықтималдылығы дегенiмiз
f(x)=F’(x)
Найти функцию распределения, выраженную через плотность распределения
Тығыздық жiктеу арқылы берiлген жiктеу функциясын табу
F(x)=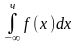
Функция распределения F(x) всегда:
F(x) функциясының жiктеуi үнемi:
0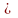 F(x)
1
F(x)
1
Математическое ожидание для непрерывной случайной величины:
Үздiксiз кездейсоқ шамаға арналған математикалық күтiм:
М(Х)=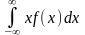
Математическое ожидание для дискретной случайной величины:
Кездейсоқ дискреттi шама үшiн математикалық күтiм:
М(Х)=
Математическое ожидание отклонения равно:
Математикалық күтiмнiң ауытқуы тең:
М[X-M(x)]=0
Выберете формулу дисперсии дискретной СВ:
Кездейсоқ дискретiк шаманың дисперсиясының формуласын таңда:
D(X)=
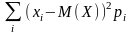
Выберете формулу дисперсии непрерывной СВ:
Үздiксiз кездейсоқ шаманың дисперсиясының формуласы:
D(X)=
Среднеквадратичное отклонение:
Орташа квадраттық ауытқу:
(x)=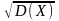
.Дифференциальное уравнение с разделенными переменными имеет вид
Айнымалылары бөлiнген дифференциял теңдеудiң түрi.
M(x)dx+N(y)dy=0
.Дифференциальное уравнение с разделяющимися переменными имеет вид
Айнымалылары бөлiнетiн дифференциял теңдеудiң түрi.
M1(x)N1(y)dx+M2(x)N2(y)dy=0
.Линейное дифференциальное уравнение первого порядка имеет вид
Бiрiншi реттi сызықты дифференциял теңдеудiң түрi.
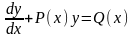
.Уравнение Бернулли имеет вид
Бернулли теңдеуiнiң түрi
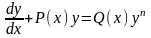
.Линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами имеет вид
Екiншi реттi тұрақты коэффициенттi дифференциял теңдеудiң түрi.
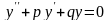
.Дифференциальное
уравнение
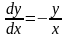 является
является
Дифференциялдық теңдеу болады
Уравнением с разделяющимися переменными
Айнымалылары бөлiнетiн теңдеу
.Екiншi реттi сызықты тұрақты коэффициеттi дифференциял теңдеу.
Дифференциальное
уравнение
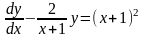 является
является
Дифференциял теєдеу болады
Линейным уравнением первого порядка
Бiрiншi реттi сызықты дифференциял теңдеу
. Указать верную формулу относительной частоты события:
Оқиғаның салыстырмалы жиiлiктiң формуласын көрсет:
w(A)=m/n
178. Тұрақты коэффициенттi екiншi реттi сызықты бiртектi дифференциял теңдеу
Дифференциальное
уравнение
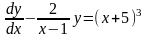 является
является
Дифференциял теєдеу болады
Линейным уравнением первого порядка
Бiрiншi реттi бiртектi сызықты теңдеу
Уравнением с разделенными переменными
Айнымалылары бјлiнген дифференциял теєдеу
Уравнением Бернулли
Бернулли теңдеуi
Однородным уравнением первого порядка
Бiрiншi реттi бiртектi теєдеу
Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами
. Тұрақты коэффициенттi екiншi реттi сызықты бiртектi дифференциял теңдеу
Дифференциальное
уравнение
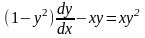 является
является
Дифференциял теєдеуболады
Уравнением Бернулли
Бернулли теңдеуi
Линейным уравнением первого порядка
Бiрiншi реттi сызықты теңдеу
Однородным уравнением первого порядка
Бiрiншi реттi бiртектi теңдеу
Уравнением с разделяющимися переменными
Айнымалылары бөлiнетiн теңдеу
Уравнением с разделенными переменными
Айнымалылары бөлiнген теңдеу
.Для
дифференциального уравнения
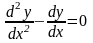 характеристическое
уравнение имеет вид
характеристическое
уравнение имеет вид
дифференциялдық теңдеу үшiн сипаттамалық теңдеудiң түрi
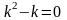
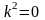
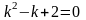
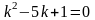
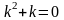
.Для
дифференциального уравнения
 характеристическое
уравнение имеет вид
характеристическое
уравнение имеет вид
дифференциялдық теңдеу үшiн сипаттамалық теңдеудiң түрi
.Для
дифференциального уравнения
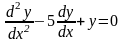 характеристическое
уравнение имеет вид
характеристическое
уравнение имеет вид
дифференциялдық теңдеу үшiн сипаттамалық теңдеудiң түрi
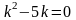
.Для
дифференциального уравнения
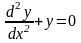 характеристическое
уравнение имеет вид
характеристическое
уравнение имеет вид
дифференциялдық теңдеу үшiн сипаттамалық теңдеудiң түрi
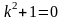

.Корнями
характеристического уравнения
дифференциального уравнения
 будут числа
будут числа
Дифференциял теңдеудiң сипаттамалық теңдеуiнiң түбiрiнiң саны
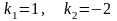
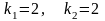
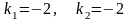
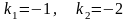
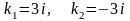
.Корнями
характеристического уравнения
дифференциального уравнения
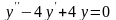 будут числа
будут числа
Дифференциял теңдеудiң сипаттамалық теңдеуiнiң түбiрiнiң саны
.Корнями
характеристического уравнения
дифференциального уравнения
 будут числа
будут числа
Дифференциял теңдеудiң сипаттамалық теңдеуiнiң түбiрiнiң саны
.Корнями
характеристического уравнения
дифференциального уравнения
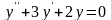 будут числа
будут числа
Дифференциял теңдеудiң сипаттамалық теңдеуiнiң түбiрiнiң саны
.Корнями
характеристического уравнения
дифференциального уравнения
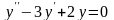 будут числа
будут числа
Дифференциял теңдеудiң сипаттамалық теңдеуiнiң түбiрiнiң саны
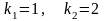
.Для
дифференциального уравнения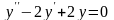 характеристическое уравнение имеет
вид
характеристическое уравнение имеет
вид
Дифференциял теңдеудiң сипаттамалық теңдеуiнiң түбiрiнiң саны
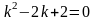

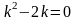
.Для дифференциального уравнения характеристическое уравнение имеет вид
Дифференциял теңдеудiң сипаттамалық теңдеуiнiң түбiрiнiң саны

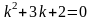
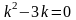
.Для
дифференциального уравнения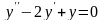 характеристическое уравнение имеет
вид
характеристическое уравнение имеет
вид
Дифференциял теңдеудiң сипаттамалық теңдеуiнiң түбiрiнiң түрі
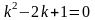

.Для
дифференциального уравнения
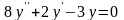 характеристическое
уравнение имеет вид
характеристическое
уравнение имеет вид
Дифференциял теңдеудiң сипаттамалық теңдеуiнiң түрi

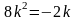

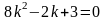
.Для
дифференциального уравнения
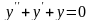 характеристическое
уравнение имеет вид
характеристическое
уравнение имеет вид
Дифференциял теңдеудiң сипаттамалық теңдеуiнiң түрi
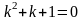
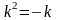
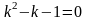
.Для
дифференциального уравнения
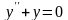 характеристическое
уравнение имеет вид
характеристическое
уравнение имеет вид
Дифференциял теңдеудiң сипаттамалық теңдеуiнiң түрi
.Для
дифференциального уравнения
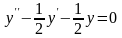 характеристическое
уравнение имеет вид
характеристическое
уравнение имеет вид
Дифференциял теңдеудiң сипаттамалық теңдеуiнiң түрi
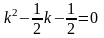
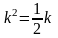
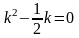
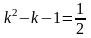
.Для дифференциального уравнения характеристическое уравнение имеет вид
Дифференциял теңдеудiң сипаттамалық теңдеуiнiң түрi
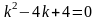
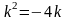



.Для
дифференциального уравнения
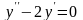 характеристическое
уравнение имеет вид
характеристическое
уравнение имеет вид
Дифференциял теңдеудiң сипаттамалық теңдеуiнiң түрi
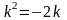
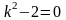
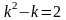
.Функция
y=f(x)
называется четной, если для
 выполняется
выполняется
y=f(x) жұп функция деп аталады егер үшiн орындалса қайсы
f(-x) = f(x)
f(-x) = - kf(x)
f(-x) = - f(x)
f(-x) = kf(x)
f(-x) = k+f(x)
.Функция y=f(x) называется нечетной, если для выполняется
y=f(x Тақ функция деп аталады егер үшiн орындалса қайсы
f(-x) = - f(x)
f(-x) = - kf(x)
f(-x) = f(x)
f(-x) = kf(x)
f(-x) = kf(x)
.Функция y=f(x) называют периодической с периодом Т неравным
нулю,
если
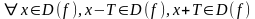 выполняется
выполняется
функциясы периодты деп аталады Т периоды нөлге тең болса,егер орындалса
f(x) = f(x+T) = f(x-T)
f(x) = f(x) / f(x+T) = f(x) / f(x-T)
f(x) = f(x) * f(x+T) = f(x) * f(x-T)
f(x) = f(x) + f(x+T) = f(x) + f(x-T)
f(x) = f(x) - f(x+T) = f(x) - f(x-T)
.Найти
область определения функции
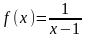
Анықталу облысын тап
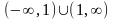

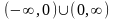

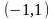
.Найти область определения функции
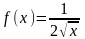
Анықталу облысын тап
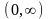

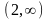
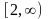
.Найти
область определения функции
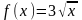
Анықталу облысын тап
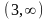
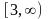
.Найти
область определения функции
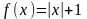
Анықталу облысын тап
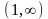

.Найти
область определения функции
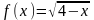
Анықталу облысын тап
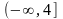
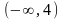
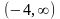
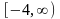
.Найти
область определения функции
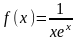
Анықталу облысын тап
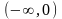
.Найти
область определения функции
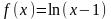
Анықталу облысын тап
.Hайти
область определения функции
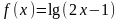
Анықталу облысын тап
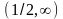
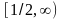

.Найти
область определения функции
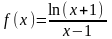
Анықталу облысын тап


.Найти
множества значений функции
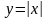
Функцияның мәнiн тап
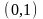
.Найти
множества значений функции

Функцияның мәнiн тап
.Найти
множества значений функции
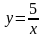
Функцияның мәнiн тап
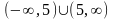
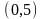
.Найти
множества значений функции
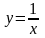
Функцияның мәнiн тап
(1,4)
.Hайти
множества значений функции
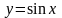
Функцияның мәнiн тап
[-1,1]
(-1,1)
(0,1)
[0,1]
.Найти
множества значений функции
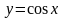
Функцияның мәнiн тап
[-1,1]
(-1,1)
(0,1)
[0,1]
.Установить четность или нечетность
функции у = х2
Функция жұп па тақ па анықта
Четная
Жұп
Нечетная
Тақ
ни четная, ни нечетная
тақта емес жұп та емес
четная и нечетная
Тақ жґне жұп
нет правильного ответа
Дұрыс жауабы жоқ
.Установить четность или нечетность
функции у = х3
Функция жұп па тақ па анықта
Нечетная
Тақ
Четная
Жұп
ни четная, ни нечетная
тақта емес жұп та емес
четная и нечетная
Тақ және жұп
нет правильного ответа
Дұрыс жауабы жоқ
.Установить четность или нечетность
функции
Функция жұп па тақ па анықта
Четная
Жұп
Нечетная
Тақ
ни четная, ни нечетная
Тақ та емес, жұпта емес
четная и нечетная
Жұп жґне тақ
нет правильного ответа
Дѕрыс жауабы жоқ
.Установить четность или нечетность
функции у = х2sin2x
Функция жұп па тақ па анықта
Нечетная
Тақ
Четная
Жұп
ни четная, ни нечетная
Тақ та емес, жұпта емес
четная и нечетная
Жұп жґне тақ
нет правильного ответа
Дұрыс жауабы жоқ
.Установить четность или нечетность
функции у = х3sin3x
Функция жұп па тақ па анықта
Четная
жұп
Нечетная
Тақ
ни четная, ни нечетная
Тақ та емес, жұпта емес
четная и нечетная
Жұп жґне тақ
нет правильного ответа
Дѕрыс жауабы жо
Установить четность или нечетность
функции у = х2cos2x
Функция жұп па тақпа анықта
Четная
жұп
Нечетная
Тақ
ни четная, ни нечетная
Тақ та емес, жұпта емес
четная и нечетная
Жұп жґне тақ
нет правильного ответа
Дѕрыс жауабы жоқ
.Установить четность или нечетность функции у = х3cos3x
Функция жұп па тақ па анықта
Нечетная
Тақ
Четная
жұп
ни четная, ни нечетная
Тақ та емес жұп та емес
четная и нечетная
Жұп жґне тақ
нет правильного ответа
Дѕрыс жауабы жоқ
.Установить четность или нечетность
функции
Функция жұп па тақ па анықта
Четная
жұп
Нечетная
Тақ
ни четная, ни нечетная
Тақ та емес жұп та емес
четная и нечетная
Жұп және тақ
нет правильного ответа
Дұрыс жауабы жоқ
.Установить четность или нечетность
функции
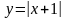
Функция жұп па тақ па анықта
ни четная, ни нечетная
Тақ та емес жұп та емес
нечетная
тақ
четная
жұп
четная и нечетная
тақ жґне жұп
нет правильного ответа
Дѕрыс жауабы жоқ
.Установить четность или нечетность
функции
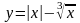
Функция жұп па тақ па анықта
ни четная, ни нечетная
Тақта емес жұпта емес
нечетная
тақ
четная
жұп
четная и нечетная
тақ және жұп
нет правильного ответа
Дұрыс жауабы жоқ
.Установить четность или нечетность
функции
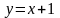
Функция жұп па тақпа анықта
ни четная, ни нечетная
Тақта емес жұпта емес
нечетная
тақ
четная
жұп
четная и нечетная
Тақта емес жұпта емес
нет правильного ответа
Дұрыс жауабы жоқ
.Вычислить
предел функции
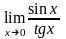
Шектi есепте
1
0
-
-1
.Вычислить
предел функции

Шеkтi есепте
0
-
3
-3
.Вычислить
предел функции

Шектi есепте
0
1/2
-
- 1/2
.Вычислить
предел функции
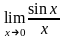
Шектi есепте
1
0
-
-1
.Вычислить
предел функции
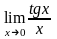
Шектi есепте
1
0
-
- 1
.Вычислить
предел функции
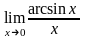
Шектi есепте
1
0
-
- 1
.Вычислить
предел функции
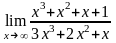
Шектi есепте
1/3
0
1
– 1/3
.Вычислить
предел функции
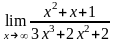
Шектi есепте
0
1/3
1
– 1/3
.Вычислить
предел функции

Шектi есепте
4
2
0
-2
.Вычислить
предел функции
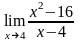
Шектi есепте
8
4
0
-4
.Вычислить
предел функции
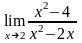
Шектi есепте
2
4
0
-4
.Вычислить
предел функции
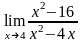
Шектi есепте
2
4
0
-4
.Вычислить
предел функции
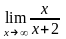
Шектi есепте
1
1/2
0
2
-2
.Вычислить
предел функции
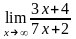
Шектi есепте
3/7
4/2
7/9
0
– 4/2
.Вычислить
предел функции
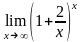
Шектi есепте
e2
e1/2
2
½
– 1/2
.Вычислить
предел функции
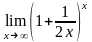
Шектi есепте
e1/2
e2
2
½
1/2
.Вычислить
предел функции
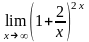
Шектi есепте
e4
e1/2
e1/4
e2
e
.Вычислить
предел функции
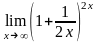
Шектi есепте
e
e2
e1/2
e4
e
.Вычислить
предел функции
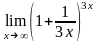
Шектi есепте
e
e3
e1/3
e6
0
.Вычислить
предел функции

Шектi есепте
1
0
-1
e
.Вычислить
предел функции

Шектi есепте
1
10
-1
–10
0
.Вычислить
предел функции
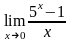
Шектi есепте
ln5
lg5
5
0
1
.Вычислить
предел функции

Шектi есепте
0
1
-1
2
.Вычислить
предел функции
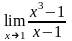
Шектi есепте
3
1
-1
0
2
.Вычислить
предел функции
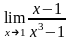
Шектi есепте
1/3
3
-1
–3
2
.Вычислить
предел функции
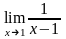
Шектi есепте
1
-1
0
2
.Вычислить
предел функции
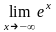
Шектi есепте
0
1
-1
2
.Вычислить
предел функции
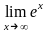
Шектi есепте
1
-1
0
2
.Найти
точки разрыва функции