48. Условный риск. Общий риск.
Введем вел-ну
- усл-е мат. ожидание потерь от принятия реш-я di при усл-и, что X=x. Эту величину наз-ют условный риск.
Введем в рассм-е функцию d(x) – каждому в-ру x ставит в соотв-е некот реш-е из мн-ва реш-й D.
-усл. мат. ожид-е потерь при усл-и, что исп. реш. ф-я d(x)
Безусловное мат ожид-е потерь при использовании решающего правила d(x) есть
R(d) наз-ся общим риском.
.
49. Постан-ка Байес. задачи решения. Оптим. реш. правило. Связь с задачей распоз-я.
Рассмотри след. экстрем. задачу: Найти такое dopt, чтобы R(d)->min. Поставленная задача решается очень просто
.
Это решающее правило наз-ся байесовским.
задача распознавания образов получается, если м/у элем-ми множ-ва d и w установим взаимооднозначное соответствие (p=m)
Реш-е заключ-ся в отнесении вектора х к одному из классов w1, w2,... ,wm.
50. Классиф-ия с минимал. вер-тью ошибки.
Рас-им случай, когда принятие любого неправил. реш-ния одинаково нежелательно.
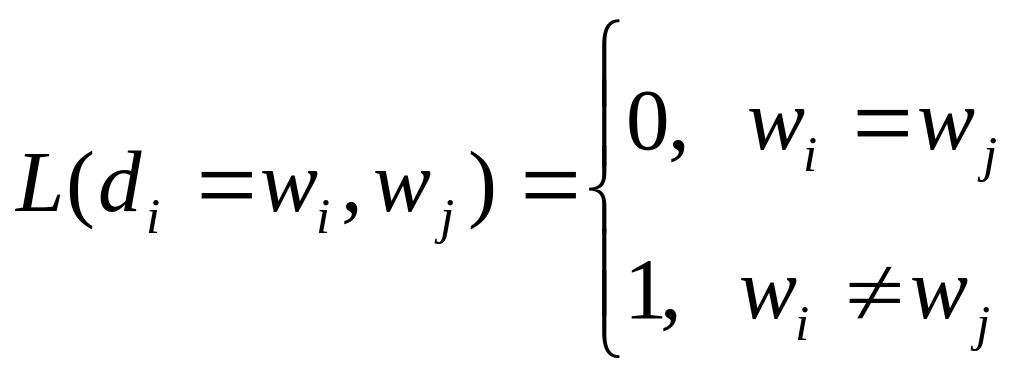
Для заданной L байесовское решающее правило будет обеспечивать min-ую вер-ть ошибки классиф-и.
R(d)=
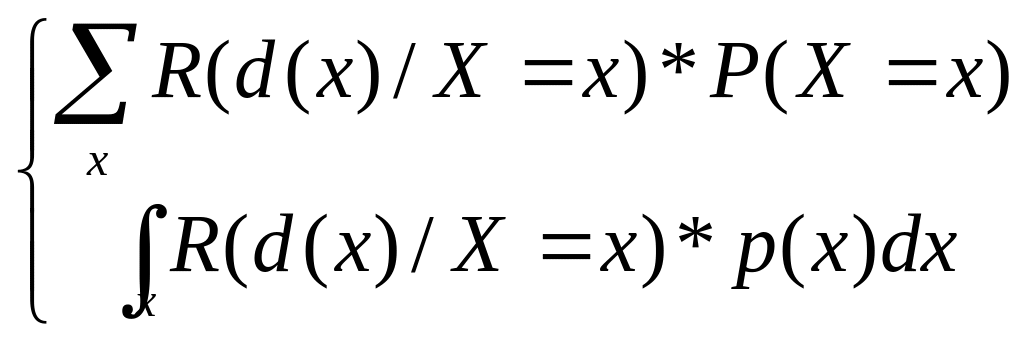=1-P(w)
– безусловная вер-ть ошибки классификации
в случае d=w.
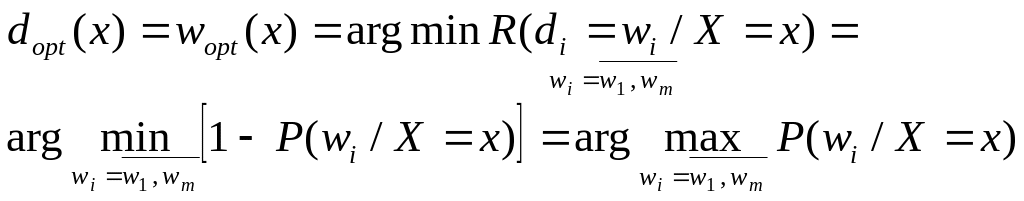
51. Минимаксное решающее правило.
-
такой набор вер-тей, при к-ром байесовский
риск принимает максим. знач-е. Т.о. d(x)
обеспечивает min-ый
риск при принятии решения в наиболее
неблагоприятной ситуации.
52. Процедура Неймана-Пирсона.
m=2. w1, w2.
X=(X1,….,Xn) при w1 имеет з-н распределения f(x), а при w2 g(x). Т.е. имеет место две гипотезы: H0: f(x), H1:g(x).
По реализации Х определить w1 или w2. Изображ-е х=(х1, …, хn) рассм-им как точку в евклидовом пр-ве R^n. Такое пр-во наз-ся пр-вом выборок. Выделим область V в R^n. Тогда любое правило м/о сформулировать так: если х в V, то Н0 следует отвергнуть (Н1 принять). Область V наз-ся критич. областью.
- ошибка 1 рода.
1-P(V/H1) – вер-ть ошибки 2 рода.
Приходим к след.
экстремальной задаче. найти V:
P(V/H1)- мощность критерия или правила.
Рассм-м R^n\T, где Т: f(x)=0; при этом условия задачи нарушены не будут.
Рассмотрим V={x:g(x)/(f(x)>=c}, c>0. c опр-ся из P{g(x)/f(x)>=c/H0}=a. Это и есть решение задачи.
f(x) наз-ся ф-я правдоподобия гипотезы Н0. g(x) - -//- H1.
g(x)/f(x) – отношение правдоподобия.
Критерий с крит. области V наз-ся процедурой Неймона-Пирсона.
53. Схема доказательства оптимальности процедуры Неймана-Пирсона.
любое правило м/о сформулировать так: если х в V, то Н0 следует отвергнуть (Н1 принять). Область V наз-ся критич. областью.
- ошибка 1 рода.
1-P(V/H1) – вер-ть ошибки 2 рода.
Приходим к след. экстремальной задаче. найти V:
Рассм-м V={x:g(x)/(f(x)>=c}, c>0. c опр-ся из P{g(x)/f(x)>=c/H0}=a.
Покажем это
P(W/H0)<=a
P(V/H0)=P(A/H0)+P(D/H0)=a
P(W/H0)=P(B/H0)+P(D/H0)<=a
P(A/H0)>=P(B/H0)
P(V/H1)=P(A/H1)+P(D/H1)=P(D/H1)+
>=P(D/H1)+
>=P(D/H1)+
>P(D/H1)+
=P(D/H1)+P(B/H1)=P(W/H1)
Т.о.P(V/H1)>P(W/H1). пр-ра Н-П. оптимальна.