18. Достоинства и недостатки методов, основанных на близости описании.
+: Простота реализации
-: Необх хранения всей обуч послед-и. Отсутствие гарантии привильного распознавания, невозможность оценки качества РП
19. Меры сходства изображений, используемые для выявления классов (кластеров).
В качестве меры м/у образами x и z м/о исп-ть:
Евклидово расстояние:
.
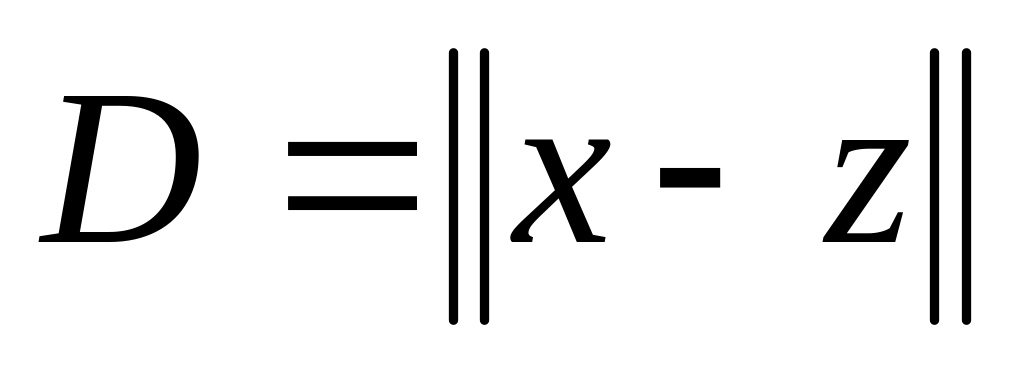чем< расстояние м/у образами, тем > сходство объектов
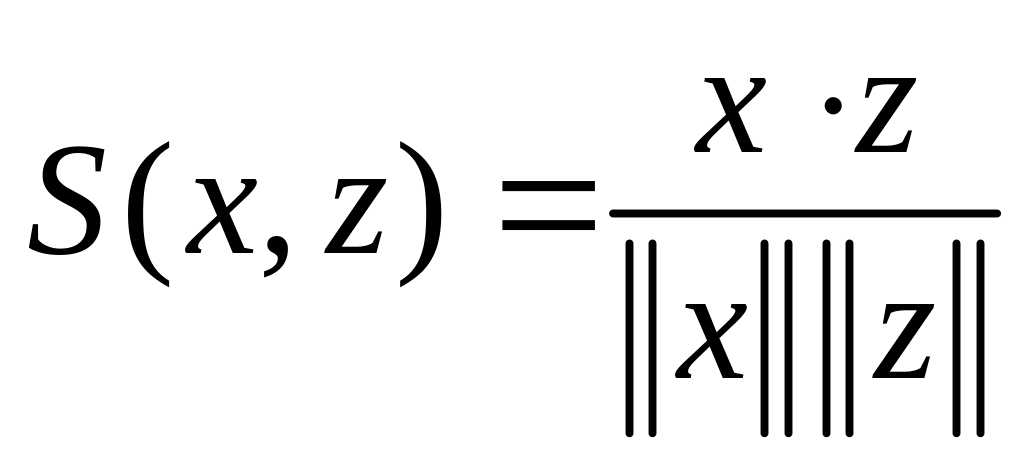косинус
угла м/у векторами,
косинус достигает мах, когда направления векторов х и z совпадают. Эту меру используют, когда кластеры распол-ся в основном вдоль осей
Мера Танимото - отношение количества совпадающих к колич-ву различ. признаков 2-х образов.
Это типичные примеры.
20. Подходы к построению процедуры классификации (кластеризации).
Эвристический подход предусматривает задание набора правил, основывающихся на использ-ии выбранной меры сходства для отнесения образов к одному из кластеров. Образ относ-ся к такому кластеру, с центром к-рого он схож в большей степени.
Подход к кластеризации, предусматривающий использование показателя качества, связан с разработкой процедур, к-рые обеспечат минимизацию или максимизацию выбранного показателя качества. Одним из наиболее популярных показателей кач-ва явл-ся сумма квадратов ошибки
где Nc—
число кластеров,Sj—
множество образов, относящихся к j-му
кластеру, а
—вектор
выборочных средних значений для мн-ва
Sj; Ni харак-ет колич-во образов, входящих
во мн-во Sj.
21. Простой эвристический алгоритм определения кластеров.
Шаг 0. Пусть задано мн-во N образов X1,…,XN. Пусть центр 1-го кластера z1 совпадает с любым из заданных образов и определена произвольная неотрицат. пороговая величина t.
Шаг 1. Вычисляется расстояние D21 м/у образом X2 и центром кластера z1 по формуле евклид. расстояния. Если D21>t, то учреждается новый центр кластера z2=X2. Иначе образ X2 включается в кластер c центром z1.
Шаг 3. Выч-ся расстояния D31 и D32 от образа X3 до центров кластеров z1 и z2. Если D31>t и D32>t, то учреждается новый центр кластера z3=X3. Иначе образ X3 зачисляется в тот кластер, чей центр к нему ближе.
Шаг m. Также расстояния от каждого нового образа до каждого известного центра кластера вычис-ся и сравн-ся с пороговой величиной—если все эти расстояния превосходят значение порога t, учреждается новый центр кластера. Иначе образ зачисляется в кластер с самым близким к нему центром.
22. Эвристический алгоритм максиминного расстояния.
Шаг 0. Пусть задано мн-во N образов X1,…,XN.
Шаг 1. Один из заданных образов назнач-ся центром первого кластера z1. Возьмем z1=X1.
Шаг 2. Затем отыскивается образ, отстоящий от образа X1 на наибольшее расстояние. Он назначается центром кластера z2.
Шаг 3. Выч-ся расстояния м/у всеми остальными образами выборки и центрами кластеров z1 и z2. В каждой паре этих расст-ий выделяется min-ое. После этого выделяется max-ое из этих min-ых расст-ий. Если последнее составляет значит. часть расс-ия м/у центрами кластеров z1 и z2, соотв-щий образ назнач-ся центром кластера z3. Иначе выполнение алгоритма прекращается.
Шаг m. В общем случае подобная проц-ра повторяется до тех пор, пока на каком-либо шаге не будет получено max-ое расстояние, для к-рого условие, определяющее выделение нового кластера, не выполняется.