55. Оценка неизвестной плотности вероятности по априорной информации

Опыт – это осуществление некоторого комплекса условий, после которого имеет место некоторый исход. Опыт считается со случайным исходом, если неизвестно каков будет исход до непосредственного проведения опыта. Численная величина, измеряющая неопределенность опыта, называется энтропией и принято ее обозначать как H.

• сформулировать и разъяснить принцип максимума энтропии, поставить задачу отыскания неизвестной плотности вероятности на основе этого принципа;

Принцип максимума энтропии утверждает, что если плотность распределения некоторой случайной величины неизвестна, то из логических соображений следует выбрать такую плотность распределения, которая обеспечивает максимизацию энтропии H случайной величины при учете всех известных ограничений.

Формула для энтропии совокупности образов, где p(x | ) – это плотность распределения случайной величины x, а – указание принадлежности образа определенному классу (дальше будем обозначать просто p(x)):

Пусть априорная информация о случайной величине x задается в виде:

и

Постановка задачи: необходимо так задать плотность распределения , чтобы величина энтропии при выполнении ограничений (2) и (3), была максимальной.

Метод множителей Лагранжа – это метод нахождения условного экстремума функции f(x), где , относительно m ограничений , где меняется от 1 до m.

Использование множителей Лагранжа позволяет из (1) построить функцию

где и для всех образов x.

Взяв частные производные от функции H₁ по плотности распределения p(x), имеем

Приравняем подынтегральное выражение к нулю и выразим из этого уравнения p(x):

p(x) = exp

Здесь множители Лагранжа следует выбирать так, чтобы они соответствовали априорной информации об образах x, содержащихся в ограничениях (2) и (3).

Исходя из полученного выражения, легко показать, что

• если случайная величина отлична от нуля только в конечном интервале, следует выбирать равномерное распределение (см. примеры)

• если случайная величина может принимать любое действительное значение, а единственными характеристиками считаются математическое ожидание и дисперсия, следует выбирать нормальное распределение(см. примеры)

56. Оценка неизвестной плотности вероятности с использованием экспериментальных данных.

(экспериментальные==апостериорные? если нет то тогда это не то)

Пусть – оценка плотности распределения . Нужно найти такую оценку, которая обеспечила бы минимизацию среднеквадратичной ошибки (интегрального квадратичного показателя качества), определяемой как

где – весовая функция. Воспользуемся разложением в ряд

где 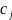- коэффициенты, подлежащие определению, а – множество заданных базисных функций.

После подстановки (8) в соотношение (7) получим

Требуется найти такие коэффициенты , которые обеспечат минимизацию интеграла вероятности ошибки .

• дать общее решение задачи;

Необходимое условие минимальности интеграла вероятности ошибки заключается в том, что . Взяв частную производную, получим

Правая часть уравнения (9) по определению равна математическому ожиданию функции . Математическое ожидание можно аппроксимировать выборочным средним, то есть

Подстановка этой аппроксимирующей оценки в уравнение (5) дает

Если базисные функции выбраны таким образом, что они ортогональны весовой функции , то из определения ортогональности следует, что

Подстановка (11) в уравнение (10) приводит к следующему соотношению, позволяющему вычислить искомые коэффициенты:

Если базисные функции ортонормированны, то для всех . Кроме того, поскольку члены не зависят от и, следовательно, для всех коэффициентов одинаковы, то их можно исключить из аппроксимирующего выражения без всякого ущерба для классификационной мощности коэффициентов. В таком случае

После того, как коэффициенты определены, с помощью формулы (4) формируется оценка плотности распределения .