Пусть теперь функция потерь неизвестна.

случайная величина.

Введем .

Тогда штук.

Выбираем среди них наименьшее: .

Тогда правило вынесения решения строится на экстремальной задаче:

Минимаксное правило для вынесения решения строится на экстремальной задаче .

52. Процедура Неймана-Пирсона

Это правило для вынесения решения, которое придумали Нейман и Пирсон, для решения задач математической статистики.

Пусть классов всего два: .

Вектор косвенных признаков получает определенную реализацию.

При этом . Требуется сконструировать распознающую процедуру, которая позволяла бы по реализации системы решить .

Модель.

Система случайных величин . Определены две гипотезы о законе распределения .

Это правило для вынесения решения относительно гипотезы и конкурирующей гипотезе при данном наблюдении.

множество возможных значений (пространство выборок). В терминах выборочного пространства структура решения такова: если реализуется системы , что , то следует отвергнуть (принять следует гипотезу ).

Тогда критическая область, которая и задает правило.

следует сделать такой, что вероятность отвергнуть гипотезу при условии, что она справедлива, являлась бы малой величиной. Это ошибка первого рода.

Но существует и ошибка второго рода – вероятность принять гипотезу при условии, что она не справедлива.

Однако область невозможность сделать такой, что оба критерия ошибок оптимизировались.

Будем выбирать область так, чтобы минимизировалась вероятность ошибки первого рода при устраивающей нас вероятности ошибки второго рода.

Процедура – экстремальная задача.

Найти область , что , где мощность критерия с критической областью для проверки против .

система дискретных случайных величин.

До проведения наблюдения мы имеем случайные величины: .

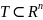
Заметим, что если в некоторой области , то автоматически присоединяем эту область к .

В дальнейшем исключим из рассмотрения область . Теперь везде

Рассмотрим область .

выбираем .

удовлетворяет решению экстремальной задачи из , то допустимое решение. Покажет теперь, что является оптимальным решением для нашей задачи.

53. Схема доказательства оптимальности процедуры Неймана-Пирсмана

показать, что любое другое правило, удовлетворяющее ограничению, хуже в смысле критерия оптимизации

От противного.

Пусть оптимум является область .

Область не пересекается с областью поэтому для справедливо .

Замечание. Из-за бесконечности область не достижимо.

Используется вся область с и часть области с .

Тогда .

Пусть функция правдоподобия , функция правдоподобия .

отношение правдоподобия.

Оптимальное правило для вынесения решения:

Это и есть процедура Неймана-Пирсона.

Случай 2.

Пусть теперь система абсолютно непрерывных случайных величин.

при верной гипотезе ; при верной гипотезе .

получение значения .

Но операции суммирования сменяются операциями интегрирования: .

Замечание. С точки зрения здравого смысла данная эвристика верна. Её оптимальность доказана.

54. Обучение байесовской процедуры распознавания: оценка неизвестных параметров.

Задана функция потерь при классификации , вероятности классов .

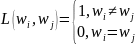
Требуются ещё условные законы распределения: .

Вероятности классов мы можем получить следующим образом:

• Через оценки ;

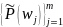• С помощью равномерного распределения ;

• С помощью минимаксного правила .

Условные законы распределения оцениваются через маркированную обучающую последовательность. Она представлена так:

Оценка законов распределения может выполняться при:

• Знании вида (формы) законов распределения;

• Незнании вида (формы) законов распределения.

Если вид законов распределения известен, то обучение Байесовской процедуры будет сводиться просто к получению состоятельной, несмещенной, эффективной оценки параметров условных законов распределения по соответствующим частям маркированной обучающей последовательности.

Получение статистических оценок параметров можно проводить любым методом.

Замечание. Гипотезу о виде законов распределения можно проверить с помощью тех же данных по любому статистическому критерию – к примеру .

Во втором же случае либо проводится аппроксимация законов распределения путем разложения их в ряд известного набора функций:

Либо от задачи минимизации общего риска переходят к задаче минимизации оценки общего риска .