Решение двух случаев.

Если имел место случай 2 (с функцией ), то тогда, начав с некоторой точки и применяя алгоритм градиентного спуска для функции , мы попадаем через некоторое количество шагов в окрестность точки . Таким образом, поставленная задача будет решена.

Если имел место случай 1, то тогда мы должны определить стратегию применения метода градиентного спуска к функциям 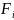такую, чтобы она обеспечивала отыскание общей точки минимума.

Искомая стратегия такова:

На первом шаге мы применяем один шаг алгоритма градиентного спуска в точке для функции . Полученное значение есть .

На втором шаге мы применяем один шаг алгоритма градиентного спуска в точке для функции , не выходя за пределы окрестности . Полученное значение есть .

…

На шаге мы применяем один шаг алгоритма градиентного спуска в точке для функции , не выходя за пределы окрестности . Полученное значение есть (переобозначим и начнём сначала).

Иначе, можно записать стратегию так:

1. Выполняется один шаг алгоритма градиентного спуска в точке для функции . Результат выполнения – .

2. Выполняется один шаг алгоритма градиентного спуска в точке для функции . Результат выполнения – .

3. 

4. Выполняется один шаг алгоритма градиентного спуска в точке для функции . Результат выполнения – .

5. Выполняется один шаг алгоритма градиентного спуска в точке для функции . Результат выполнения – .

7. Выполняется один шаг алгоритма градиентного спуска в точке для функции . Результат выполнения – .

Процесс останавливается, когда при прохождении всей последовательности функций значения вектора не меняются.

Отметим, что применение такой стратегии не гарантирует успех, даже если общая точка минимума функций существует.

Однако, для некоторых классов функций эта стратегия оказывается успешной.

42. Алгоритм обучения перцептрона как реализация специальной стратегии совместной минимизации нескольких функций с помощью градиентных методов.

Отметим, что применение такой стратегии (см. 40, 41)не гарантирует успех, даже если общая точка минимума функций существует.

Однако, для некоторых классов функций эта стратегия оказывается успешной. Покажем, что успехом применения такой стратегии является алгоритм обучения перцептрона (успех доказывается теоремой Новикова).

Укажем соответствия с введенными здесь обозначениями:

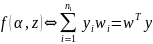
Для случая с преобразованной обучающей последовательностью :

.

Функции имеют следующий вид: .

Отметим, что все эти функции неотрицательны: .

Отметим также, что для любого любая такая функции имеет единственный минимум, равный , при .

Напишем один шаг алгоритма градиентного спуска при фиксированном значении .

Тогда мы получаем знакомое правило на шаге:

Отметим, что . Тогда конечный алгоритм запишется так:

При начальных параметрах мы получаем алгоритм обучения перцептрона. Сходимость этого алгоритма гарантируется теоремой Новикова.

43. Физическая интерпретация метода потенциальных функций

При построении систем классификации образов аналитическими методами первоочередной задачей является определение решающих функции, которые порождают в пространстве образов границы, отделяющие образы, принадлежащие различным классам.

Предположим, что требуется разделить два непересекающихся образа w₁ и w₂. Это значит, что в пространстве изображений существует, по крайней мере, одна функция, которая полностью разделяет множества, соответствующие образам w₁ и w₂. Эта функция должна принимать положительные значения в точках, соответствующих объектам, принадлежащим образу V₁, и отрицательные - в точках образа V₂. В общем случае таких разделяющих функций может быть много, тем больше, чем компактней разделяемые множества. В процессе обучения требуется построить одну из этих функций, иногда в некотором смысле наилучшую.

Метод потенциальных функций связан со следующей процедурой. В процессе обучения с каждой точкой пространства изображений, соответствующей единичному объекту из обучающей последовательности, связывается функция K(x, x_k), заданная на всем пространстве и зависящая от x_k как от параметра. Такие функции называются потенциальными, так как они напоминают функции потенциала электрического поля вокруг точечного электрического заряда. Изменение потенциала электрического поля по мере удаления от заряда обратно пропорционально квадрату расстояния. Потенциал, таким образом, может служить мерой удаления точки от заряда. Когда поле образовано несколькими зарядами, потенциал в каждой точке этого поля равен сумме потенциалов, создаваемых в этой точке каждым из зарядов. Если заряды, образующие поле, расположены компактной группой, потенциал поля будет иметь наибольшее значение внутри группы зарядов и убывать по мере удаления от нее.

Можно считать, что кластер, образованный выборочными образами, принадлежащими классу w₁, образует «плато», причем выборочные образы размещаются на вершинах некоторой группы холмов. Подобную геометрическую интерпретацию можно ввести и для образов класса w₂. Эти два «плато» разделены «долиной», в которой, как считается, потенциал падает до нуля. На основе таких интуитивных доводов создан метод потенциальных функций, позволяющий при проведении классификации определять решающие функции.