Часть 1.
Строится нерекурсивная грамматика, порождающая в точности заданное множество выборочных цепочек. Выборочные цепочки обрабатываются в порядке уменьшения длины.
Правила подстановки
строятся и прибавляются к грамматике
по мере того, как они становятся нужны
для построения соответствующей цепочки
из выборки. Заключительное правило
подстановки, используемое для порождения
самой длинной выборочной цепочки,
называется остаточным
правилом, а длина его
правой части равна 2. Остаточное правило
длины
имеет вид
,
где
— нетерминальный символ, а
—терминальные элементы.
Предполагается, что остаток каждой цепочки максимальной длины является суффиксом (хвостовым концом) некоторой более короткой цепочки. Если какой-либо остаток не отвечает этому условию, цепочка, равная остатку, добавляется к обучающей выборке.
Из последующих рассуждений будет ясно, что выбор остатка длины 2 не связан с ограничением на алгоритм. Можно выбрать и более длинный остаток, но тогда потребуется более полная обучающая выборка в связи с условием, что каждый остаток является суффиксом некоторой более короткой цепочки.
В нашем примере первой
цепочкой максимальной длины в обучающей
выборке является цепочка
.
Для порождения этой цепочки строятся
следующие правила подстановки:
,
где —правило остатка.
Вторая цепочка —
.
Правила для порождения этой цепочки
строятся аналогично.
Поскольку цепочка и предыдущая цепочка имеют одинаковую длину, требуется остаточное правило длины 2. Заметим также, что работа первой части алгоритма приводит к некоторой избыточности правил подстановки. Но в первой части мы занимаемся лишь определением множества правил подстановки, которое способно в точности порождать обучающую выборку, и не касаемся вопроса избыточности. В сложных ситуациях трудно соблюдать выполнение этого условия и одновременно уменьшать число необходимых правил подстановки. Значительно проще просматривать введенные правила слева направо, чтобы определить, будут ли они порождать новую цепочку, не стремясь при этом минимизировать число правил подстановки. Об устранении избыточности речь пойдет в третьей части алгоритма.
Окончательно множество правил подстановки, построенных для порождения обучающей выборки, выглядит следующим образом:
Часть 2.
В этой части, соединяя
каждое правило остатка длины 2 с другим
(неостаточным) правилом грамматики,
получаем рекурсивную
автоматную грамматику.
Это происходит в результате слияния
каждого нетерминального элемента
правила остатка с нетерминальным
элементом неостаточного правила, который
может порождать остаток. Так, например,
если
— остаточный нетерминал вида
и
— неостаточный нетерминал вида
,
где
,
все встречающиеся
заменяются на
,
а правило подстановки
отбрасывается.
Таким способом создается автоматная грамматика, способная порождать данную обучающую выборку, а также обладающая общностью, достаточной для порождения бесконечного множества других цепочек.
В рассматриваемом примере выделим остаточные правила:
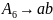
Для правила
проведем поиск кандидата на слияние.
Это правила вида
.
Здесь подходят следующие правила:
Таким образом, мы
сливаем нетерминал
с нетерминалом
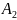и удаляем правило
(а также повторяющиеся правила):
Для правила проведем поиск кандидата на слияние. Здесь подходят следующие правила:
Таким образом, мы
сливаем нетерминал
с нетерминалом
и удаляем правило
(а также повторяющиеся правила):
.
Рекурсивными правилами
являются
и
.