3. Классификация на основе синтаксического анализатора:

Достоинства: требуется минимум информации (так как грамматика – компактное представление языка), информация в грамматике о языке всегда полная.

Недостатки: сложность вывода для обобщенных грамматик.

63. Задача восстановления грамматики по обуч выборке

Грамматика будет конструироваться по представителям своего языка . Кроме того, есть недопустимые представители – цепочки . Рассмотрим грамматику как строящуюся грамматику .

маркированная выборка – множество цепочек алфавита что либо , либо . 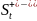содержит принадлежащих языку представителей, содержит не принадлежащих языку представителей.

При увеличении объема выборки появляются новые представители: .

Грамматика строится таким образом, что : допускаемые цепочки из выводимы в грамматике ; пропускаемые цепочки из не выводимы в грамматике .

Задача восстановления грамматики называется разрешимой, если существует алгоритм, который за конечное число шагов может построить грамматику 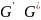, что начиная с .

Замечания. Существует не единственная грамматика, которая эквивалентна (является решением задачи восстановления грамматики).

Если задано множество грамматик и в нём грамматика , и если алгоритм формирует грамматики из множества , то будем говорить, что алгоритм перечисляет множество .

64. Информаторное представление задачи расп

Будем говорить, что задача восстановления грамматики дана в информаторном представлении, если:

1. 

2. 

3. 

65. Текстуальное

Будем говорить, что задача восстановления грамматики дана в текстуальном представлении, если:

1. 

2. 

66. Теор о разрешимости

Теорема о разрешимости задачи для информаторного представления.

Пусть произвольное множество разрешимых грамматик. Тогда при информаторном представлении задача восстановления грамматики разрешима для любой грамматики из .

67. Теор о неразр

Теорема о неразрешимости для текстуального представления.

Рассмотрим множество грамматик всех конечных языков и 1 грамматики, порождающей бесконечный язык. Тогда не существует алгоритма, который для произвольной грамматики из данного множества решает задачу восстановления грамматики.

Отметим, что множество является перечислимым множеством грамматик, так как содержит все грамматики, порождающие конечные языки, и только одну грамматику, порождающую бесконечный язык.

68. Два класса алг восст грамм

Алгоритмы восстановления грамматик можно разделить на 2класса:

• алгоритмы восстановления грамматики перечислением;

• алгоритмы восстановления грамматики индукцией.

Алгоритмы восстановления грамматики перечислением не могут быть эффективны, т.к. грамматики в перечисляются независимо от выборки.

Алгоритмы восстановления грамматики индукцией используют подход, который заключается в построении достаточно простой грамматики на основе изучения выборки так, чтобы

Наиболее известным примером алгоритма восстановления грамматики индукцией является алгоритм Фельдмана.

69. Алг Фельдмана

Алгоритм можно разделить на три части. Первая часть формирует нерекурсивную грамматику. Вторая часть преобразует её в рекурсивную грамматику. Затем, в третьей части, происходит упрощение этой грамматики.

Рассмотрим выборочное множество терминальных цепочек . Требуется получить автоматную грамматику, способную порождать эти цепочки. Алгоритм построения грамматики состоит из следующих этапов.