37. Перцептрон и его математическая модель.

Перцептрон – устройство, моделирующее работу мозга человека.

Существует три типа элементов в перцептроне:

элементы	Играют роль рецепторов, воспринимающих сигналы внешней среды.
элементы	Воспринимают сигнал от группы прикрепленных элементов; вырабатывают сигнал, если совокупное воздействие входов превосходит некоторое пороговое значение.
элементы	Соответствуют каждый определенному классу; любой элемент вырабатывает сигнал – линейную комбинацию входов.

где коэффициенты усиления.

Перцептрон относит к тому классу, в соответствие с которым поставлен элемент с наибольшим значением выходного сигнала.

Обучение перцептрона заключается в установлении таких значений каждого элемента, при которых перцептрон осуществляет безошибочную классификацию предъявленной маркированной обучающей последовательности.

Существует много разные типов перцептронов, отличающихся воспринимающими элементами, системой связи, количеством слоев элементов, процедурами обучения.

Математическая модель перцептрона.

Будем рассматривать только случай (количество классов ограничено). Тогда будет достаточно 1 элемента.

Признаки подаются на элементы в виде вектора .

.

вектор весов. Тогда .

разделяющая гиперповерхность. Принадлежность тому или иному подпространству исходного пространства означает принадлежность тому или иному классу (всего два варианта).

уравнение гиперплоскости, проходящей через начало координат. спрямляющее пространство.

38. Алгоритм обучения перцептрона

граница раздела между двумя классами.

Обучение перцептрона сводится к определению весовых коэффициентов на основе маркированной обучающей последовательности таким образом, чтобы эта обучающая последовательность правильно классифицировалась перцептроном.

мерных векторов.

значение вектора весов на шаге алгоритма.

элемент обучающей последовательности, используемый на шаге алгоритма. В процессе работы алгоритма может быть пройдено алгоритмом неоднократно. корректирующее приращение.

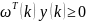Рассмотрим ый шаг алгоритма. Если и , то . Если и , то . Если ни одно условие из двух не выполнилось, оставляем вектор без изменений: .

Алгоритм заканчивает свою работу, если вся обучающая последовательность проходиться без изменений вектора весов.

Замечание 1. Алгоритм обучения перцептрона реализует известный в биологии принцип подкрепления – наказания, когда наказание – изменение весов и продолжение работы; подкрепление – отсутствие наказания.

Замечание 2. Разделяющая гиперплоскость в спрямляющем пространстве проходит через начало координат. Однако, разделение обучающей последовательности такой гиперплоскостью не всегда возможно. В этом случае переходят к пополненному спрямляющему пространству.

В дальнейшем будем считать, что такое пополнение спрямляющего пространства при необходимости уже сделано.

Замечание 3. Наряду с исходной обучающей последовательностью будем рассматривать преобразованную обучающую последовательность – , в которой . Тогда ый шаг алгоритма запишется так: если , то , иначе .