1.Предмет фин мата.

Изучает финансовые операции в которых есть необходимость использования финансо-эконом вычеслений, возникай всякий раз когда в условии сделки имеется:Даты,сроки,переодичности поступления денежных средств.

2.Наращенная сумма ренты.

Наращенная сумма ренты – сумма всех членов последовательности рентных платежей с начисленными на них процентами к концу срока ренты.

3.Инвистиции

Инвистиции:Ден средства,ценные бумаги,иное имущество вкладываемое в обьекты предпринимательской деятельности в целях получения прибыли.

Косвенные,прямые.

Виды:Краткосрочные,среднесрочные,долгосрочные

1<1,5>3.

Косвенные,прямые.

4. Сущность простых процентов состоит в том, что они начисляются на одну и ту же величину капитала К в течение всего срока ссуды.

5.О современной стоимости ренты, как уже отмечалось, нужно произвести дисконтирование величин ее элементов или, иными словами, найти их современные стоимости.

6)% ставка –это сумма ,указанная в процентном выражении сумме кредита, которую платит получатель кредита использования им в расчете на опред.период. %ставка=сумма начисленного процента/первоначальная сумма.

7) Эта схема соответствует процедуре дисконтирования, т.е. проценты начисляются не в конце, а в начале каждого периода, точкой отсчета является наращенная сумма Sn, и расчет ведется справа налево. Наращенные суммы при учетной ставке d изменяются следующим образом:

Sn-1=Sn-In = Sn(1-d);

Sn-2=Sn-1(1-d)= Sn(1-d)2;

………………………………..;

K=S1(1-d)= Sn(1-d)n.

Отношение начального и наращенного капиталов

Dn=K/Sn=(1-d)n (2.3)

называется коэффициентом дисконтирования. По определению он обратен коэффициенту наращения , или

And= 1/Dn=Sn/K=(1-d)-n (2.4)

Если принять равными процентную и учетную ставки, то антисипативный расчет сложных процентов дает больший доход, чем декурсивный. В самом деле, отношение

= An/And=(1+i)n(1-d)n

при d=i

= (1-i2)n<1,

что доказывает приведенное утверждение. Эквивалентная же дисконтная ставка оказывается всегда меньше процентной

При решении задачи нахождения по заданному доходу текущей величины при заданной доходности и в общем случае при кратном начислении применяют формулу:

.

В этом случае дисконт составляет

.

При смешанной схеме применяют формулу математического дисконтирования-

8)S=P(1+ni) Капитал ложится на определенный срок в долг,рассчитывая на получение дохода от этой сделки.Размер зависит от 3 факторов :величина капитала, от срока,от величину ссудного %.Наращение по простой %-прямая операция.

9)1-годовая рента .2-p-срочная рента.3-рента с периодом больше года.

10)Все и так знают.английская-365/365,французская -360/365 ,германская-360/360.

11) Коэффициент наращения ренты - отношение наращенной суммы ренты к сумме ее годовых платежей или к размеру отдельного платежа.

12)При выдаче кредита или при изменении банк может выставлять разные ставки.В этом случае % платежи суммируются при вычислении наращенной суммы.(ежедневные ,ежегодные,ежемесяч,квартальные).

13)При описании фин.рент часто используются универсальные показатели, не завищащие от денежных велечин платежной ренты и имеющие между народные обозначение.

Пост нумерандо. Sni= S(N) деленное R= 1+i в (N степени) -1 деленное на i.

И пренумерандо sni=S1(n) деленное R= (1+i)( 1+i)(в N степени)-1 деленное i

14)Процесс начисления и удержания % вперед(в виде дисконта)называют учетом. 2 принципа:1)путем наращения суммы 2)устанавливая скидку с конечной суммы долга

15)индекс рентабельности-рассчитывается как отношение суммы дисконт.денежных потоков к первонач.инвестициям .Он характеризует уровень дохода на единицу затрат т.е эффективность вложения.

16)Дисконт-уступка,скидка,сбавка. Разница между ценой ,по которой ценная бумага продается на фонд .бирже в данный момент и текущем биржевом курсе.

17)Виды эффективности проекта:1)эффективность проекта в целом 2)эффективность участия в проекте 1)оценивается с целью определения потенциальной привлекательности проекта 2)определяется его финансовая реализуемость, и заинтересованность участников.

18)Число, показывающее во сколько раз наращенная сумма

долга больше первоначальной, называется множителем наращения (или

множителем накопления)

Простая учетная ставка иногда применяется и при расчете наращенной суммы. Например, при определении суммы, которую надо проставить в векселе, если задана текущая сумма долга.

Множитель наращения: 

19)Консолидированные платежи-это объединение нескольких платежей в один.

20)Этот метод дисконтирования применяется в основном при банковском учете векселей.Проценты начисляются на сумму ,подлежащую уплате в конце срока операции .База при дискон.учетной ставке: 360/360 или 360/365

21)?---------------

22?---------------

23)Срок окупаемости-период времени,необходимый для того,чтобы доходы, генерируемые инвестициями,покрыли затраты на инвестиции.

24)----------------

25)Внутренняя норма прибыльности-это процентная ставка,при котрой чистый дисконтированный доход,равен 0. NPV рассчитывается на основании потока платежей, дисконтированного к сегодняшнему дню.

26)Сложные проценты начисляются на увеличивающеюся с каждым периодом начисления базу.

27)-----------------------

28)Два способа начисления сложных процентов: 1)антисипативный-(в начале периода начисляются %)2)декурсивный- (в конце периода начисляются %).

29)Параметры фин.рент-1-член ренты-величина каждого определенного платежа 2-Период ренты-временной интервал.3-% ставка –ставка используемая при наращении и дисконтирование образующих ренту ,число платежей в году ,число начислений процентов в году ,моменты платежа внутри периода ренты.

30. Декурсивный расчет сложных процентов при годовой капитализации. При декурсивном (обычном) начислении сложных процентов процентные платежи рассчитываются в конце каждого периода на сумму, накопленную в предыдущем периоде.

31. В чём бы ни заключалась та или иная конкретная задача финансовой математики, в её условии всегда будет присутствовать некий набор денежных выплат. Даже самая тривиальная финансовая операция — простая ссуда — содержит два платежа: выдачу ссуды и её возврат. Эти два платежа, рассматриваемые в совокупности, представляют собой простейший пример денежного потока, или потока платежей.

32. Коэффициент наращения.

Выражение 1 / (1 + i)n называется коэффициентом дисконтирования. Очевидно, он равен величине, обратной величине коэффициента наращения.

33. Эквивалентными считаются такие платежи, которые, будучи «приведенными» к одному моменту времени, оказываются равными. Приведение осуществляется путем дисконтирования (приведение к более ранней дате) или, наоборот, наращения платежа (если дата относится к будущему). Если при изменении условий контракта указанный принцип не соблюдается, то одна из сторон контракта терпит ущерб, размер которого можно заранее определить.

34. Сравним множители наращения по простой и сложным процентным ставкам. При

сроке большем нуля и меньше года множитель наращения по простой процентной

ставке превосходит множитель наращения по сложной:

(1+ni) > (1+i)n

При сроке больше года множитель наращения по сложной прцентной ставке больше

множителя по простой:

(1+ni) < (1+i)n

При сроках, равных нулю и единице, множители наращения по сложным и простым

процентам равны.

35.Эквивалентность процентных ставаок.

Процентные и учетные ставки решают одни и те же задачи: определяют степень доходности при операции наращения или размеры дисконтированных сумм при учетных операциях. В связи с этим возможен выбор таких процентных или учетных ставок, при использовании которых финансовые последствия окажутся равноценными.

Равноценность финансовых последствий может быть обеспечена в том случае, если наблюдается равенство множителей наращения или дисконтных множителей.

36. Дикурсивная,антипативная ставка.

При декурсивном (обычном) начислении сложных процентов процентные платежи рассчитываются в конце каждого периода на сумму, накопленную в предыдущем периоде. При годовой капитализации в конце каждого года имеем наращенные суммы:

Sn-1=Sn-In = Sn(1-d); Проценты начисляются не в конце, а в начале каждого периода, точкой отсчета является наращенная сумма Sn, и расчет ведется справа налево. Наращенные суммы при учетной ставке d изменяются следующим образом:

37. Чистая текущая стоимость, чистый дисконтированный доход, англ. Net present value, принятое в международной практике анализа инвестиционных проектов сокращение — NPV или ЧДД) — это сумма дисконтированных значений потока платежей, приведённых к сегодняшнему дню. Показатель NPV представляет собой разницу между всеми денежными притоками и оттоками, приведенными к текущему моменту времени (моменту оценки инвестиционного проекта)

38. ну я сегодня положил бабло, 100 евро

через год 10% 110 евро

а на след год 10% от 110 процентов

39.Изминение контрактов.

В практике возникают случаи, когда необходимо заменить одно финансовое обязательство другим. Общепринятым принципом, исходя из которого должны происходить изменения условий контрактов, является финансовая эквивалентность обязательства, которая предполагает неизменность (эквивалентность) финансовых отношений сторон до и после изменения условий. Эквивалентными считаются такие платежи, которые, будучи "приведенными" по заданной процентной ставке к одному моменту времени, оказываются равными. Приведение разновременно выплачиваемых сумм денег осуществляется путем их дисконтирования или, наоборот, наращения.

40.Коэф.дикурсивных процентов

An=Sn/K= (1+i)n (2.2)

называется коэффициентом наращения капитала (A – accumulation). Он показывает, во сколько раз возрастает за n лет каждая единица кредита К (например, одна гривна). По сравнению с коэффициентом наращения Anпр=Sn/K= 1+in при начислении простых процентов коэффициент (2.2) оказывается меньше при n<1, равным при n=1 и больше при n>1, причем с ростом n выигрыш нарастает.

41. Выплаты с вашей стороны например, когда у вас долг, и вы должны учитывать оплату долга +оплата процентов и прочее, а так-же наоборот.

42.Капитализация.

При декурсивном (обычном) начислении сложных процентов процентные платежи рассчитываются в конце каждого периода на сумму, накопленную в предыдущем периоде. При годовой капитализации в конце каждого года имеем наращенные суммы:

S1=K+I1, I1=Ki;

S2=S1+I2, I2=S1i;

S3=S2+I3, I3=S2i;

43.RX 1(1+i)-n(степень)/i

44. 7 ,18,21,22,24,27,44

45 Вопрос:

Уравнение эквивалентности – уравнение, устанавливающее равенство соответствующих эквивалентных значений потоков.

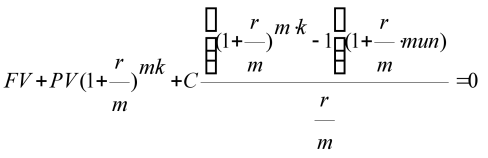
Из этого уравнения можно определить одну из величин как функцию остальных:

FV=f(PV,С,r,m,k) – будущую сумму в любой момент;

PV=f(FV,С,r,m,k) – текущую сумму, пересчитанную к любому моменту финансовой сделки;

С=f(PV,FV,r,m,k) – выплаты;

k=f(PV,FV,С,r,m) – срок договора;

r=f(PV,FV,С,m,k) – норму, годовую процентную ставку.

Уравнение эквивалентности – уравнение, устанавливающее равенство соответствующих эквивалентных значений потоков.

46 Вопрос:

Эффективная процентная ставка — это сложная процентная ставка по кредиту, рассчитанная в предположении, что все платежи, необходимые для получения данного кредита, идут на его погашение.

Если задана номинальная процентная ставка, и капитализация процентов осуществляется m раз в год, то за год сумма вклада увеличится в

(1+jm)m раз.

Найденная таким образом сложная процентная ставка называется «эффективной», так как она, в отличие от номинальной ставки, характеризует настоящую доходность (эффективность) ссудной операции. Отметим, что эффективная учетная ставка всегда меньше номинальной.

Номинальная ставка – это объявленная кредитной организацией процентная ставка. S=P(1+j/m)N

Вопрос 47:

Периодические платежи могут осуществляться в конце периода - постнумерандо (обыкновенные) или в начале периода - пренумерандо.

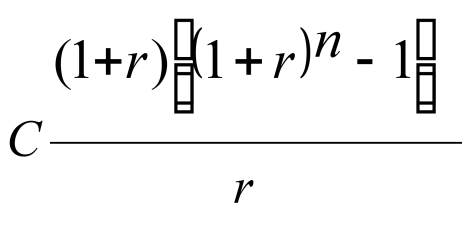
формулы можно объединить в одну:

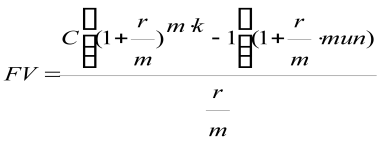
Вопрос 48:

Дисконтирование может производиться не один раз в году, а m раз в год, т. е. каждый раз учет производится по ставке  . В этом случае где f – номинальная годовая учетная ставка.

Эффективная учетная ставка d показывает степень дисконтирования за год. Ее определяют из равенства дисконтных множителей.

Эффективная учетная ставка меньше номинальной при m > 1.

Вопрос 49:

Поток платежей, все члены которого положительные величины, а временные интервалы постоянны, называют финансовойрентой или аннуитетом. Финансовая рента имеет следующие параметры: член ренты – величина каждого отдельного платежа, период ренты – временной интервал между двумя соседними платежами, срок ренты – время, измеренное от начала финансовой ренты до конца ее последнего периода, процентная ставка – ставка, используемая при наращении или дисконтировании платежей, образующих ренту, число платежей в году, число начислений процентов в году, моменты платежа внутри периода ренты.

По времени выплаты первого аннуитетного платежа различают:

аннуитет постнумерандо — выплата осуществляется в конце первого периода,

аннуитет пренумерандо — выплата осуществляется в начале первого периода.

Коэффициент аннуитета превращает разовый платёж сегодня в платёжный ряд. С помощью данного коэффициента определяется величина периодических равных выплат по кредиту:

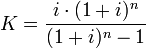
Вопрос 50:

Эквивалентные процентные ставки – такие ставки, значения, которых в конкрет­ных условиях приводят к одинаковым финансовым результа­там, т.е. замена одного вида ставки на другой при соблюдении принципа эквивалентности не изменяет финансо­вых отношений сторон в рамках одной операции. , , где n – срок в годах, i_s – ставка простых процентов, d_s – простая учетная ставка.

Процентная и учетная ставки эквивалентны, если они имеют одинаковый коэффициентнаращения A_n=1+in=1/(1-dn). Отсюда легко получить: i=d/(1-dn),) d=i/(1+in). Из этого следует, что эквивалентные простые процентная и учетная ставки зависят от срока n кредитования.

51

Рента – ряд последовательных фиксированных платежей, производимых равные промежутки времени.

По числу начисления процентов различают:

- ренты с начислением раз в год;

-ренты с начислением m раз в год;

- непрерывное начисление;

52

Две ставки называются эквивалентными, если при замене одной ставки на другую финансовые отношения сторон не меняются.

53

Одним из условий кредитного договора является способ его погашения. Долг может погашаться разными способами: в конце срока; по частям в течение срока; проценты – по частям, а основной долг – в конце срока кредитного договора и др. В зависимости от выбора способа погашения кредита сумма процентных денег будет различной.

Частным случаем погашения долга равными срочными уплатами является потребительский кредит, при котором проценты начисляются по простой ставке. При р выплатах в году сумма выплаченных процентов

                                                                                                    

   где D – сумма кредита; S – годовая ставка простых процентов по кредиту; п – срок кредита в годах.

    Общая сумма расходов по погашению кредита составит

                                                                                                                        

и, следовательно, размер одинаковых очередных взносов

                                                                   

54

Платежи по методу выплат выделяют:

- Постнумерандо (с выплатой в конце периода);

- Пренумернадо (с выплатой в начале периода);

55

Доходность портфеля ценных бумаг

Портфель ценных бумаг представляет собой совокупность различных ценных бумаг, и доходность его можно определить по следующей формуле:

 

Доходность _{портфеля} = (Стоимость ценных бумаг _{на момент расчета} – Стоимость ценных бумаг _{на момент покупки}) / Стоимость ценных бумаг _{на момент покупки}.

 Риск портфеля объясняется не только индивидуальным риском каждой отдельно взятой ценной бумаги портфеля, но и тем, что существует риск воздействия изменений наблюдаемых ежегодных величин доходности одной акции на изменение доходности других акций, включаемых в инвестиционный портфель.

56

57

Планирование погашение долга заключается в определении периодических расходов связанных с займом, так же расходы называют обслуживанием долга, а разовая сумма обслуживания долга – срочная уплата, в которую входят:

Текущие % платежа;

Средства для погашения основной суммы долга

58

Современная(текущая) величина потока платежей – это сумма платежей, дисконтированных на момент начала ренты по ставке начисляемых сложных процентов.

Если сумма долга определяется на какой-либо момент в будущем (FVA), тогда величину последующих взносов в течении N лет при начислении на них процентов по ставке I можно определить по формуле:

R=FVA* i / (1+i)ⁿ-1

59

60. Учёт векселя - это покупка векселя банком по цене ниже вексельной суммы, с дисконтом.

определяется по формуле:   , где

 — сумма дисконта;

 — вексельная сумма;

 — количество дней до даты погашения векселя;

 — учётная ставка банка.

61. Портфель (англ. portfolio) ценных бумаг — совокупность инвестиционных вложений юридического или физического лица.

Основными задачами инвестиционного портфеля являются:

• обеспечение устойчивого заданного уровня дохода;

• минимизация риска или удержание его на заданном уровне;

• снижение операционных затрат;

• решение специфических задач, постановка которых невозможна вне совокупности ценных бумаг.

Портфель дохода формируется из ценных бумаг, обеспечивающих получение высокого текущего дохода — процентных и дивидендных выплат. Его цель — систематическое получение дохода на инвестированный в ценные бумаги капитал. Существуют следующие его основные разновидности:

• портфель регулярного дохода ориентирован на получение среднего уровня дохода на капитал при минимальном уровне риска;

• портфель доходных бумаг состоит, как правило, из высокодоходных облигаций корпораций или вообще ценных бумаг, приносящих высокий доход при среднем уровне риска.

Риск портфеля ценных бумаг является вероятностью, что ожидания владельца портфеля касательно его доходности могут и не оправдаться, и тогда часть доходов получена не будет.

63.Деньги, взятые на долгосрочные капитальные вложения правило, погашается в серии ежегодных, полугодовых или ежемесячных платежей. Есть несколько способов для расчета суммы этих платежей:

1. равный общей суммы платежей за определенный период времени (амортизация);

2. равный основной сумме долга за определенный период времени, или

3. равными платежами в течение определенного периода времени с воздушного шара платеж в конце, чтобы погасить остаток.

64. Антисипативный расчет сложных процентов при годовой капитализации,т.е.проценты начисляются не в конце, а в начале каждого периода, точкой отсчета является наращенная сумма S_n, и расчет ведется справа налево. Наращенные суммы при учетной ставке d.

65.

66.  Планирование погашения задолженности, кредита или ссуды заключается в определении периодических расходов по займу, т.е. размеров срочных уплат. Срочные уплаты охватывают как текущие процентные платежи, так и средства, предназначенные для погашения основного долга.

Актуарный метод предполагает последовательное начисление процентов на фактические суммы долга.

Метод торговца –

67.