20. Циркуляция векторного поля и ротор векторного поля. Вычисление ротора в декартовых координатах.

Циркуляцией векторного поля называется криволинейный интеграл второго рода, взятый по произвольному замкнутому контуру L:

Где — векторное поле (или вектор-функция), определенное в некоторой области D, содержащей в себе контурL,— бесконечно малое приращение радиус-векторавдоль контура. Окружность на символе интеграла подчёркивает тот факт, что интегрирование производится по замкнутому контуру.

Циркуляция по контуру, ограничивающему несколько смежных поверхностей, равна сумме циркуляций по контурам, ограничивающим каждую поверхность в отдельности, то есть

–формула Стокса в векторном виде.

Вихревым вектором (вихрем) или ротором векторного поля называется вектор, имеющий координаты:

Ротор в декартовых координатах:

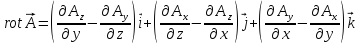
Если , то векторное поленазывается безвихревым или потенциальном.

21. Оператор Гамильтона (набла), дифференциальные операции второго порядка, связь между ними.

Оператор набла (оператор Гамильтона) – векторный дифференциальный оператор, обозначаемый символом . Для трёхмерного евклидова пространства в прямоугольных декартовых координатах оператор набла определяется следующим образом:

22. Основные понятия, относящиеся к оду первого порядка: общее и частное решения, общий интеграл, интегральные кривые. Задача Коши, её геометрический смысл.

Дифференциальным уравнением называется соотношение , в которомx – независимая переменная, y – искомая функция. Это обыкновенное дифференциальное уравнение (ОДУ) первого порядка.

–уравнение, разрешённое относительно производной.

f(x,y) – заданная, непрерывная в некоторой области D переменных (x,y) функция.

Пусть . График функцииназываетсяинтегральной кривой, –изоклины кривые.

Пусть правая часть уравнения (*) не зависит от y, то есть , тогда.

На рисунке представлено семейство интегральных кривых, зависящих от одного параметра C.

Пусть . Будем считать независимой переменнойy, а x – функция от y, то есть . Тогда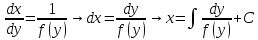. Но еслии это уравнение имеет корень, то добавляется решение, которое надо добавить к общему семейству, зависящему от параметраC.

Всякая функция вида при подстановке в (*), после чего (*) становится тождеством, является решением (общим решением дифференциального уравнения (*)).

Если C взято равным конкретному числу, то решение φ(x,C₀) называется частным решением уравнения (*). - отсюда находится значениеC.

Условие Коши – когда указано, какому x₀ соответствует y₀. Задача Коши: – условие уравнения + условие Коши, то есть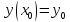. Задачу Коши геометрически можно сформулировать так: среди всех интегральных кривых уравнения (*) найти ту кривую (рисунок слева), которая проходит через заданную точку (x₀, y₀).

Пример. Дано: и. Решить задачу Коши.

Когда , то:

–частное решение задачи Коши.

23. Интегрирование оду первого порядка с разделяющимися переменными и однородных.

Уравнением с разделенными переменными называется дифференциальное уравнение вида: с непрерывными функциямиf(х) и g(y). Равенство , гдеC — произвольная постоянная, определяет общий интеграл уравнения с разделёнными переменными.

Принцип решения таких уравнений:

Если дано условие Коши, то есть и, то. Еслии уравнение имеет корень, то это решение добавляется к основному семейству.

Определение однородной функции. Функция f(x,y) называется однородной функцией своих переменных x и y, если, каково бы ни было число , выполняется следующее:, гдеp – степень (показатель) однородности. Например, – однородная функция, степень однородности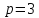, так как. Степеньp может быть равной нулю, если .

Уравнение называетсяоднородным, если функция, стоящая в правой части, является однородной функцией своих переменных. Пусть f(x,y) будет однородной функцией степени 0, то есть . Пусть, тогда. Уравнения такого типа решаютсязаменой (переходом к новой функции): .

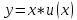
–общее решение.

Если , а, то:

Если , то уравнениеимеет кореньu₀, тогда: – решение: – прямая наряду с семейством.

Общий вид однородного уравнения, если его записать в виде дифференциалов:

То есть M(x,y) и N(x,y) должны быть однородными функциями одной и той же степени однородности.