36. Линейно-зависимые и линейно-независимые системы функций. Необходимое условие линейной зависимости. Теорема об определителе Вронского решений однородного линейного оду.

Вопрос убран.

37. Теорема об общем решении (о структуре общего решения) однородного линейного оду.

Линейное однородное ОДУ: .

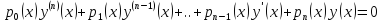Теорема о структуре общего решения линейного однородного уравнения:

Если все коэффициенты уравнения линейного однородного дифференциального уравнения непрерывны на отрезке [a;b] , а функции y₁(x), y₂(x),..., y_n(x) линейно независимые решения этого уравнения, то общее решение уравнения имеет вид , гдеC₁,...,C_n — произвольные постоянные.

38. Теорема об общем решении (о структуре общего решения) неоднородного линейного оду.

Неоднородное линейное ОДУ: , где .

Краткое определение теоремы для заучивания: Для нахождения общего решения неоднородного уравнения достаточно найти одно какое-нибудь частное решение этого уравнения и прибавить к нему общее решение соответствующего однородного уравнения.

Формулировка по-другому: Если все коэффициенты уравнения линейного однородного дифференциального уравнения непрерывны на отрезке [a;b], а функции y₁(x), y₂(x),..., y_n(x) образуют фундаментальную систему решений соответствующего однородного уравнения, то общее решение неоднородного уравнения имеет вид:

где C₁,...,C_n — произвольные постоянные, y*(x) — частное решение неоднородного уравнения.

39. Метод вариации произвольных постоянных для отыскания частных решений неоднородного линейного оду.

Рассмотрим линейное неоднородное дифференциальное уравнение 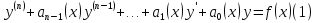с непрерывными на [a; b] коэффициентами и непрерывной правой частью. Предположим, что известна фундаментальная система решений соответствующего однородного уравнения (2). Будем искать частное решение неоднородного уравнения в виде где- неизвестные,n раз дифференцируемые на [a; b] функции. Их называют варьируемые постоянные общего решения однородного уравнения.

Пусть — фундаментальная система решений однородного уравнения  (2) с непрерывными на отрезке [a;b] коэффициентами. Если правая часть f(x) неоднородного уравнения  (1) непрерывна на [a; b], то его частное решение можно искать в виде:

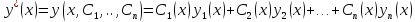Неизвестные функции находятся из системы:Такой метод называетсяметодом вариации произвольных постоянных или методом Лагранжа.

40. Фундаментальная система решений однородного линейного оду с постоянными коэффициентами в случае простых корней характеристического уравнения, действительных или комплексных.

Вопрос убран.

41. Фундаментальная система решений однородного линейного оду с постоянными коэффициентами в случае, когда имеются кратные корни характеристического уравнения.

Вопрос убран.

42. Отыскание частных решений неоднородного линейного оду с постоянными коэффициентами и специальной правой частью.

Неоднородное линейное ОДУ: , где

Уравнение (*) имеет справа неоднородность f(x) специального вида, т.е. типа решений однородного уравнения 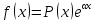, где(не разбирали, что такоеP), α – постоянное число вещественное или комплексное. Общее решение неоднородного уравнения в этом случае есть сумма общего решения однородного уравнения плюс частное решение неоднородного, которое надо искать в виде , гдеQ(x) – многочлен той же степени, что и P(x) (если α – НЕ (!!) корень характеристического многочлена).

Абзац из учебника. (не разбирали). Коэффициенты полиномаQ(x) определяются подстановкой в (*) и приравниванием коэффициентов при одинаковых степеняхx в левой и правой частях полученного равенства. Искомые коэффициенты найдутся и притом единственным образом, так что уравнение (*) имеет только одно частное решение вида .

Если же α совпадает с корнем характеристического многочлена кратности r, то частное решение неоднородного уравнения надо искать в виде , гдеQ имеет такой же вид, как написано выше. Коэффициенты тоже определяются подстановкой в (*).

Пример.

Найдём решение однородного уравнения:

, ,

,

Общее решение однородного уравнения:

а) Найдём частное неоднородное первое решение, то есть:

б) Найдём частное неоднородное второе решение, то есть:

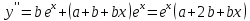
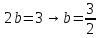
Ответ: .