32. Теорема об общем решении (о структуре общего решения) нормальной системы неоднородных линейных оду.

Рассмотрим неоднородную линейную систему обыкновенных дифференциальных уравнений n-го порядка

 Здесь A

Справедлива следующая теорема о структуре общего решения этой неоднородной линейной системы ОДУ.

Если матрица A(x) и вектор-функция b(x) непрерывны на [a, b], и пусть Φ(x) — фундаментальная матрица решений однородной линейной системы , то общее решение неоднородной системыY' = A(x)Y + b(x) имеет вид:

где C — произвольный постоянный вектор-столбец, x₀ — произвольная фиксированная точка из отрезка [a, b].

Из приведенной формулы легко получить формулу решения задачи Коши для линейной неоднородной системы ОДУ — формулу Коши.

Решением задачи Коши ,Y(x₀) = Y₀ является вектор-функция

33. Метод вариации произвольных постоянных для отыскания частных решений нормальной системы неоднородных линейных оду.

Определение системы неоднородных линейных ОДУ. Система ОДУ вида:

называется линейной неоднородной. Пусть

Система (*) в векторно-матричном виде: .- система однородная, иначе – неоднородная.

Сам метод. Пусть имеется линейная неоднородная система , тогда- линейная однородная система, соответствующая линейной неоднородной. Пусть– фундаментальная матрица системы решений,, гдеC – произвольный постоянный вектор, - общее решение системы. Станем искать решение системы (1) в виде, гдеC(x) – неизвестная (пока) вектор-функция. Хотим, чтобы вектор-функция (3) была решением системы (1). Тогда должно быть справедливо тождество:

(произвольный постоянный вектор, который получается в результате интегрирования, можно считать равным 0). Здесь точки x₀, – любые.

Видим, таким образом, что если в (3) в качестве C(t) брать , то вектор-функциябудет решением системы (1).

Общее решение линейной неоднородной системы (1) может быть записано в виде . Пусть требуется найти решение системы (1), удовлетворяющее начальному условию. Подстановка (4) начальных данных (5) даёт. Следовательно, решение задачи Коши (1)-(5) может быть записано в виде:. В частном случае, когда, последняя формула принимает вид:.

34. Фундаментальная система решений нормальной системы однородных линейных оду с постоянными коэффициентами в случае простых действительных корней характеристического уравнения.

Нормальная линейная однородная система n порядка с постоянными коэффициентами - или,Коэффициенты линейных комбинаций искомых функций постоянны. Эта система в матричной форме–матричная форма, гдеA-постоянная матрица. Матричный метод: Из характеристического уравнения найдем различные корни и для каждого корня (с учетом его кратности) определим соответствующее ему частное решение .Общее решение имеет вид: . При этом 1) если - действительный корень кратности 1, то , где -собственный вектор матрицы А, соответствующий собственному значению, то есть. 2) – корень кратности , то соответствующее этому корню решение системы ищут в виде вектора(**), коэффициенты которого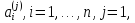определяются из системы линейных уравнений, получающихся приравнивание коэффициентов при одинаковых степеняхx в результате подстановки вектора (**) в исходную систему.

Фундаментальной системой решений НЛОС называется совокупность произвольных n линейно независимых решений

35. Фундаментальная система решений нормальной системы однородных линейных ОДУ с постоянными коэффициентами в случае, когда все корни характеристического уравнения простые, но имеются комплексные корни.

Вопрос убран.