
- •Определение двойного интеграла и его основные свойства.
- •Сведение двойного интеграла к повторному.
- •Тройной интеграл, сведение его к повторному.
- •Криволинейные координаты на плоскости и в пространстве. Координатные линии и поверхности. Полярные, цилиндрические и сферические координаты.
- •Замена переменных в двойном интеграле. Пример: случай полярных координат.
- •Замена переменных в тройном интеграле. Примеры: случаи цилиндрических и сферических координат.
- •Вычисление площади гладкой поверхности, заданной параметрически и в явном виде. Элемент площади поверхности.
- •Определение криволинейного интеграла первого рода, его основные свойства и вычисление.
- •Определение криволинейного интеграла второго рода, его основные свойства и вычисление. Связь с интегралом первого рода.
- •Формула Грина. Условия того, что криволинейный интеграл на плоскости не зависит от пути интегрирования.
- •Определение поверхностного интеграла первого рода, его основные свойства и вычисление.
- •Определение поверхностного интеграла второго рода, его основные свойства и вычисление. Связь с интегралом первого рода.
- •Теорема Гаусса-Остроградского, её запись в координатной и векторной (инвариантной) формах.
- •Теорема Стокса, её запись в координатной и векторной (инвариантной) формах.
- •Условия того, что криволинейный интеграл в пространстве не зависит от пути интегрирования.
- •Скалярное поле. Градиент скалярного поля и его свойства. Вычисление градиента в декартовых координатах.
- •Определение векторного поля. Поле градиента. Потенциальные поля, условия потенциальности.
- •Поток векторного поля через поверхность. Определение дивергенции векторного поля и её свойства. Вычисление дивергенции в декартовых координатах.
- •Соленоидальные векторные поля, условия соленоидальности.
- •Циркуляция векторного поля и ротор векторного поля. Вычисление ротора в декартовых координатах.
- •Оператор Гамильтона (набла), дифференциальные операции второго порядка, связь между ними.
- •Основные понятия, относящиеся к оду первого порядка: общее и частное решения, общий интеграл, интегральные кривые. Задача Коши, её геометрический смысл.
- •Интегрирование оду первого порядка с разделяющимися переменными и однородных.
- •Интегрирование линейных оду первого порядка и уравнений Бернулли.
- •Интегрирование оду первого порядка в полных дифференциалах. Интегрирующий множитель.
- •Метод введения параметра. Интегрирование оду первого порядка Лагранжа и Клеро.
- •Простейшие оду высших порядков, интегрируемые в квадратурах и допускающие понижение порядка.
- •Нормальная форма системы линейных оду, скалярная и векторная (матричная) запись. Задача Коши для нормальной системы линейных оду, её геометрический смысл.
- •Линейно-зависимые и линейно-независимые системы вектор-функций. Необходимое условие линейной зависимости. Теорема об определителе Вронского решений системы однородных линейных оду.
- •Теорема об общем решении (о структуре общего решения) нормальной системы неоднородных линейных оду.
- •Метод вариации произвольных постоянных для отыскания частных решений нормальной системы неоднородных линейных оду.
- •Фундаментальная система решений нормальной системы однородных линейных оду с постоянными коэффициентами в случае простых действительных корней характеристического уравнения.
- •Линейно-зависимые и линейно-независимые системы функций. Необходимое условие линейной зависимости. Теорема об определителе Вронского решений однородного линейного оду.
- •Теорема об общем решении (о структуре общего решения) однородного линейного оду.
- •Теорема об общем решении (о структуре общего решения) неоднородного линейного оду.
- •Метод вариации произвольных постоянных для отыскания частных решений неоднородного линейного оду.
- •Фундаментальная система решений однородного линейного оду с постоянными коэффициентами в случае простых корней характеристического уравнения, действительных или комплексных.
- •Фундаментальная система решений однородного линейного оду с постоянными коэффициентами в случае, когда имеются кратные корни характеристического уравнения.
- •Отыскание частных решений неоднородного линейного оду с постоянными коэффициентами и специальной правой частью.
- •Теорема существования (локальная) решения задачи Коши для оду первого порядка.
- •Теорема единственности решения задачи Коши для оду первого порядка.
1.Определение двойного интеграла и его основные свойства. 3
2.Сведение двойного интеграла к повторному. 4
3.Тройной интеграл, сведение его к повторному. 5
4.Криволинейные координаты на плоскости и в пространстве. Координатные линии и поверхности. Полярные, цилиндрические и сферические координаты. 6
5.Замена переменных в двойном интеграле. Пример: случай полярных координат. 7
6.Замена переменных в тройном интеграле. Примеры: случаи цилиндрических и сферических координат. 8
7.Вычисление площади гладкой поверхности, заданной параметрически и в явном виде. Элемент площади поверхности. 11
8.Определение криволинейного интеграла первого рода, его основные свойства и вычисление. 12
9.Определение криволинейного интеграла второго рода, его основные свойства и вычисление. Связь с интегралом первого рода. 14
10.Формула Грина. Условия того, что криволинейный интеграл на плоскости не зависит от пути интегрирования. 17
11.Определение поверхностного интеграла первого рода, его основные свойства и вычисление. 18
12.Определение поверхностного интеграла второго рода, его основные свойства и вычисление. Связь с интегралом первого рода. 20
13.Теорема Гаусса-Остроградского, её запись в координатной и векторной (инвариантной) формах. 22
14.Теорема Стокса, её запись в координатной и векторной (инвариантной) формах. 24
15.Условия того, что криволинейный интеграл в пространстве не зависит от пути интегрирования. 26
16.Скалярное поле. Градиент скалярного поля и его свойства. Вычисление градиента в декартовых координатах. 27
17.Определение векторного поля. Поле градиента. Потенциальные поля, условия потенциальности. 28
18.Поток векторного поля через поверхность. Определение дивергенции векторного поля и её свойства. Вычисление дивергенции в декартовых координатах. 29
19.Соленоидальные векторные поля, условия соленоидальности. 30
20.Циркуляция векторного поля и ротор векторного поля. Вычисление ротора в декартовых координатах. 31
21.Оператор Гамильтона (набла), дифференциальные операции второго порядка, связь между ними. 32
22.Основные понятия, относящиеся к ОДУ первого порядка: общее и частное решения, общий интеграл, интегральные кривые. Задача Коши, её геометрический смысл. 33
23.Интегрирование ОДУ первого порядка с разделяющимися переменными и однородных. 34
24.Интегрирование линейных ОДУ первого порядка и уравнений Бернулли. 36
25.Интегрирование ОДУ первого порядка в полных дифференциалах. Интегрирующий множитель. 37
26.Метод введения параметра. Интегрирование ОДУ первого порядка Лагранжа и Клеро. 40
27.Простейшие ОДУ высших порядков, интегрируемые в квадратурах и допускающие понижение порядка. 43
28.Основные понятия, относящиеся к системам ОДУ: порядок системы, нормальная форма системы, общее и частное решения, общий и первый интегралы. Задача Коши для нормальной системы, её геометрический смысл. 45
29.Нормальная форма системы линейных ОДУ, скалярная и векторная (матричная) запись. Задача Коши для нормальной системы линейных ОДУ, её геометрический смысл. 47
30.Линейно-зависимые и линейно-независимые системы вектор-функций. Необходимое условие линейной зависимости. Теорема об определителе Вронского решений системы однородных линейных ОДУ. 48
31.Фундаментальные системы решений нормальной системы однородных линейных ОДУ. Теорема существования фундаментальных систем. Теорема об общем решении (о структуре общего решения) нормальной системы однородных линейных ОДУ. 49
32.Теорема об общем решении (о структуре общего решения) нормальной системы неоднородных линейных ОДУ. 50
33.Метод вариации произвольных постоянных для отыскания частных решений нормальной системы неоднородных линейных ОДУ. 51
34.Фундаментальная система решений нормальной системы однородных линейных ОДУ с постоянными коэффициентами в случае простых действительных корней характеристического уравнения. 53
35.Фундаментальная система решений нормальной системы однородных линейных ОДУ с постоянными коэффициентами в случае, когда все корни характеристического уравнения простые, но имеются комплексные корни. 54
36.Линейно-зависимые и линейно-независимые системы функций. Необходимое условие линейной зависимости. Теорема об определителе Вронского решений однородного линейного ОДУ. 54
37.Теорема об общем решении (о структуре общего решения) однородного линейного ОДУ. 55
38.Теорема об общем решении (о структуре общего решения) неоднородного линейного ОДУ. 56
39.Метод вариации произвольных постоянных для отыскания частных решений неоднородного линейного ОДУ. 57
40.Фундаментальная система решений однородного линейного ОДУ с постоянными коэффициентами в случае простых корней характеристического уравнения, действительных или комплексных. 58
41.Фундаментальная система решений однородного линейного ОДУ с постоянными коэффициентами в случае, когда имеются кратные корни характеристического уравнения. 58
42.Отыскание частных решений неоднородного линейного ОДУ с постоянными коэффициентами и специальной правой частью. 59
43.Теорема существования (локальная) решения задачи Коши для ОДУ первого порядка. 61
44.Теорема единственности решения задачи Коши для ОДУ первого порядка. 61
Определение двойного интеграла и его основные свойства.
Определение
двойного интеграла.
Пусть на плоскости XY
задана функция
 и область (P)
(область задания функции f(x,y)),
её площадь P.
Произведём разбиение площади сеткой
кривых Pi,
где Pi
– частичная
область. Внутри частичной области
возьмём произвольную точку с координатами
(ξi,ηi).
Составим интегральную сумму:
и область (P)
(область задания функции f(x,y)),
её площадь P.
Произведём разбиение площади сеткой
кривых Pi,
где Pi
– частичная
область. Внутри частичной области
возьмём произвольную точку с координатами
(ξi,ηi).
Составим интегральную сумму:
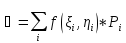 .
Пустьλ
– характеристика
разбиения,
которая равна
.
Пустьλ
– характеристика
разбиения,
которая равна
 ,
гдеdi
– диаметр частичной области. Диаметр
– максимальное расстояние между любой
парой точек в области. Устремим λ
к нулю. Если существует предел интегральных
сумм
,
гдеdi
– диаметр частичной области. Диаметр
– максимальное расстояние между любой
парой точек в области. Устремим λ
к нулю. Если существует предел интегральных
сумм
 ,
то этот предел и называетсядвойным
интегралом:
,
то этот предел и называетсядвойным
интегралом:
 .
.
Основные свойства двойного интеграла:
Свойство аддитивности:

Свойства линейности:
а)

б)

Модуль интеграла меньше или равен интегралу от модуля:

Теорема о среднем. Так как
 ,
то, проинтегрировав это неравенство,
получим:
,
то, проинтегрировав это неравенство,
получим:



 ,
где
,
где
 .
.
Сведение двойного интеграла к повторному.
Теорема.
Если функция f(x,
y)
интегрируема в
прямоугольнике,
указанном на рисунке, и если  и существует интеграл
и существует интеграл ,
тогда существует повторный интеграл
,
тогда существует повторный интеграл и
он равен двойному:
и
он равен двойному: =
= .
.
Замечание.
Если f(x,
y)
интегрируема в прямоугольнике, указанном
на рисунке, и  и существует интеграл
и существует интеграл тогда
существует повторный интеграл
тогда
существует повторный интеграл .
.
Предположим, что
область D
произвольного
вида. Делаем
разбиение и проводим параллельные
линии. Заключим область (D)
в прямоугольник (D*),
 ,
и в нём определим функциюf*(x,y):
,
и в нём определим функциюf*(x,y):
 .
.

Формула в общем
виде:
 .
Так же доказывается, что
.
Так же доказывается, что .
.
Тройной интеграл, сведение его к повторному.
Определение
тройного интеграла.
Пусть в некоторой области (V)
с границей (S)
задана в каждой точке функция f(x,y,z).
Разобьём тело (V)
сеткой поверхностей на частичные области
(Vi).
В каждой (Vi)
возьмём произвольную точку (ξi,
ηi,
ζi)
и составим интегральную сумму:
 .
Устремим максимальный диаметр (макс.
расстояние между любой парой точек в
области) к нулю:
.
Устремим максимальный диаметр (макс.
расстояние между любой парой точек в
области) к нулю: .
Тогда, если существует предел интегральных
сумм, то он равен тройному интегралу:
.
Тогда, если существует предел интегральных
сумм, то он равен тройному интегралу: .
.
На
всякий случай
определение
интегральной суммы.
Пусть на
нек-ом отрезке
 задана
задана .
Произведём разбиение отрезка:
.
Произведём разбиение отрезка: .
Число
.
Число ,
называетсяинтегральной
суммой функции
f(x),
соответствующей данному разбиению
T(ξi;xi)
сегмента [a;b]
и данному выбору промежуточных точек
ξi
на частичных
сегментах [xi-1;xi],
Δ
–хар-тика разбиения:
,
называетсяинтегральной
суммой функции
f(x),
соответствующей данному разбиению
T(ξi;xi)
сегмента [a;b]
и данному выбору промежуточных точек
ξi
на частичных
сегментах [xi-1;xi],
Δ
–хар-тика разбиения:

Сведение к
повторному интегралу.
Рассмотрим первый
простейший случай.
Пусть тело V
– прямоугольный параллелепипед. Проведём
секущую плоскость. Возьмём приращение
плоскости (жирные линии). Тогда:
 .
.
Рассмотрим второй
случай.

Рассмотрим третий случай – область (V) цилиндрического типа.


Криволинейные координаты на плоскости и в пространстве. Координатные линии и поверхности. Полярные, цилиндрические и сферические координаты.
Криволинейная
система координат
— система координат в евклидовом
(аффинном) пространстве, или в области,
содержащейся в нём. Применяются обычно
на плоскости
( )
и впространстве
(
)
и впространстве
( ),
гдеn
–размерность пространства (равно числу
координат). Пусть
),
гдеn
–размерность пространства (равно числу
координат). Пусть
 -область
евклидова пространства E.x,y,z-
декартовы координаты в этом пространстве.
-область
евклидова пространства E.x,y,z-
декартовы координаты в этом пространстве.
 -область евклидова пространства
-область евклидова пространства ,
, декартовы координаты
декартовы координаты .Рассмотрим
однозначное и взаимно непрерывное
отображение области
.Рассмотрим
однозначное и взаимно непрерывное
отображение области
 на область
на область ,
которое осуществляется посредством
функций:
,
которое осуществляется посредством
функций:

В области
 вводятся криволинейные координаты
вводятся криволинейные координаты .
ТочкаM
определяется тройкой чисел
.
ТочкаM
определяется тройкой чисел
 .
Если фиксированы какие-либо координаты
(например
.
Если фиксированы какие-либо координаты
(например ),
то при переменном
),
то при переменном эти соотношения определяют в области
эти соотношения определяют в области некоторую линию, отличную от прямой –это координатная
линия
некоторую линию, отличную от прямой –это координатная
линия
 .Производные
.Производные
 вычисленные
в точке M,
представляют собой координаты вектора
касательной к линии
вычисленные
в точке M,
представляют собой координаты вектора
касательной к линии
 в этой точке (вектор
в этой точке (вектор ).
).
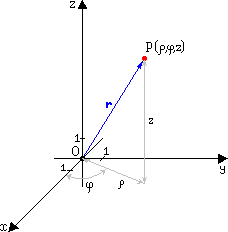
Цилиндрическая
система координат
 ,
, .
Таким образом,
.
Таким образом, ,
, .
(
.
(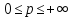 ,
, ,
, .
Эти неравенства определяют на евклидовом
пространстве бесконечную область
.
Эти неравенства определяют на евклидовом
пространстве бесконечную область .
Для цилиндрических координаткоординатными
поверхностями
являются плоскости, перпендикулярные
к оси Oz (z=const), полуплоскости, ограниченные
осью z
(
.
Для цилиндрических координаткоординатными
поверхностями
являются плоскости, перпендикулярные
к оси Oz (z=const), полуплоскости, ограниченные
осью z
( ),
и цилиндрические поверхности, осью
которых является ось z (
),
и цилиндрические поверхности, осью
которых является ось z ( ).Координатные
линии – линии
пересечения этих поверхностей.
).Координатные
линии – линии
пересечения этих поверхностей.
Сферическая система
координат:
 ,
,
 .
. ,
, .
Координаты
.
Координаты тоже
тоже :
(
:
( ,
, ,
, .Координатные
поверхности:
сферы с центром в начале (
.Координатные
поверхности:
сферы с центром в начале ( ),
полуплоскости, ограниченные осью z
(φ=const), конусы (с вершиной в начале), для
которых ось z является осью (θ=const).Координатные
линии – линии
пересечения этих поверхностей.
),
полуплоскости, ограниченные осью z
(φ=const), конусы (с вершиной в начале), для
которых ось z является осью (θ=const).Координатные
линии – линии
пересечения этих поверхностей.
Полярными
координатами точки P
называются радиус-вектор ρ – расстояние
от точки P до заданной точки O (полюса) и
полярный угол φ – угол между прямой OP
и заданной прямой, проходящей через
полюс (полярной осью). Координатные
линии в полярных
системах – окружности с центром в полюсе
и лучи.
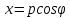 ,
, .
.
