Лекции + ответы на экзамен (3 семестр) / Обязательные вопросы

1. Определение двойного интеграла

Пусть на плоскости XY задана функция и область (P) (область задания функции f(x,y)), её площадь P. Произведём разбиение площади сеткой кривых P_i, где P_i – частичная область. Внутри частичной области возьмём произвольную точку с координатами (ξ_i,η_i). Составим интегральную сумму: . Пусть λ – характеристика разбиения, которая равна , где d_i – диаметр частичной области. Диаметр – максимальное расстояние между любой парой точек в области. Устремим λ к нулю. Если существует предел интегральных сумм , то этот предел и называется двойным интегралом: .

2.Определение криволинейного интеграла первого рода.

Дана простая кривая, то есть . Пусть кривая будет разбита точками разбиения. Составим интегральную сумму..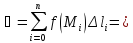

- криволинейный интеграл первого рода.

На словах можно сказать так. Если существует предел интегральной суммы (см. выше) при стремлении к нулю наибольшей из длин Δl_k (то есть 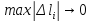), то этот предел называется криволинейным интегралом первого рода от функции f(x,y) по кривой L и обозначается символом или .

3. Определение криволинейного интеграла второго рода.

Пусть на кривой AB заданы две функции, P(x, y) и Q(x, y). Разобьем сегмент на n частей точками . Кривая АВ разобьется на n частей точками в направлении от A к B. Пусть – координаты точки , ,, – длина дуги . На каждой дуге возьмем некоторую точку (координаты ) и составим две интегральные су­ммы: , . Если существует предел интегральной суммы при стремлении к нулю наибольшей из длин , то этот предел называется криволинейным интегралом второго рода . Сумма называется общим криволинейным интегралом второго рода.

4. Формула Грина. Пусть заданы функции P(x,y) и Q(x,y), которые непрерывны в области D вместе с частными производными первого порядка. Интеграл по границе (L), целиком лежащий в области D и содержащий все точки в области D: –общая формула Грина.

5. Определение поверхностного интеграла первого рода. Спроектируем S на плоскость xy, получим область D. Разобьём область D сеткой линий на части, называемые . Из каждой точки каждой линии проведём параллельные z линии, тогда и S разделится на . Составим интегральную сумму: . Устремим максимум диаметра к нулю: , получим: Это поверхностный интеграл первого рода.

Определение вкратце. Если существует конечный предел интегральной суммы, не зависящий от способа разбиения S на элементарные участки S_i и от выбора точек, то он называется поверхностным интегралом первого рода.

6. Определение поверхностного интеграла второго рода. Рассмотрим в пространстве XYZ двухстороннюю поверхность S, состоящую из конечного числа кусков, каждый из которых либо задан уравнением вида z=f(x,y), либо является цилиндрической поверхностью с образующими, параллельными оси ОZ. Пусть R(x,y,z)-функция, определенная в точках поверхности S. Разобьем поверхность S на n частей ,не имеющих общих внутренних точек и таких, что каждая часть умещается на однои из кусков поверхности S. Обозначим через -площади поверхности на XOY. Возьмем на каждой часть поверхности S произвольную точку .

Cумма всех таких произведений –интегральная сумма для функции R(x,y,z) по поверхности S по переменным x и у. Если при стремлении к нулю шага разбиения поверхности S интегральные суммы имеют предел, то этот предел называется поверхностным интегралом (второго рода) по выбранной стороне поверхности S от функции R(x,y,z) по переменным x и у: . Аналогичным образом определяются поверхностные интергралы второго рода по выбранной стороне S по переменным y и z (z и x). Если существуют интерграллы по всем переменным : . – общий вид.

7. Теорема Гаусса-Остроградского. Пусть в замкнутой ограниченной области (V) заданы функции P(x,y,z), Q(x,y,z) и R(x,y,z), непрерывные на (V) вместе со своими частными производными первого порядка. Тогда имеет место следующее тождество: .

8. ОДУ первого порядка с разделяющимися переменными и однородных. Дифференциальным уравнением называется соотношение , в котором x – независимая переменная, y – искомая функция. Это обыкновенное дифференциальное уравнение (ОДУ) первого порядка. – уравнение, разрешённое относительно производной. С разделяющимися переменными(принцип решения): ; ; ; .

Общий вид однородного уравнения, если его записать в виде дифференциалов:

. То есть M(x,y) и N(x,y) должны быть однородными функциями одной и той же степени однородности. Уравнения такого типа решаются заменой (переходом к новой функции): ;;; ;;– общее решение.

9. Линейные ОДУ первого порядка и уравнения Бернулли.

ДУ первого порядка называется линейным, если неизвестная функция y(x) и её производная y’(x) входят в уравнение в первой степени: . P(x), Q(x) – непрерывные функции. Уравнение однородное, если Q(x)=0.

. Окончательно неоднородное уравнение будет иметь вид:.

Уравнение Бернулли: . Принцип решения:;

Если обозначить за Z(x), то . Отсюда . Подставим это выражение выше и получим:

.Получили дифференциальное линейное уравнение.

10. ОДУ первого порядка в полных дифференциалах. Интегрирующий множитель. Полных диффернциалах: . Если левая часть есть дифференциал некоторой функции u(x,y): – общий интеграл уравнения; если , а , то критерий полного дифференциала . Найдём эту функцию u. Пусть , тогда . Так как , то:. Отсюда находится φ'(y). Если оказалось НЕ уравнением в полных дифференциалах. Возникает вопрос, существует ли функция μ(x,y), которая: становится полным дифференциалом, где μ – интегрирующий множитель. Методику решений, пример см. в лекциях.

11. Метод введения параметра. Для уравнений не разрешенных относительно производной (1) : . Если из уравнения y можно выразить, то есть , то это решается методом введения параметра, а именно: Обозначим , получим: Продифференцируем по x:; ; ; . Получили уравнение, разрешённое относительно производной. p(x,C) подставляем в (*), получим: . Это и будет решение.

Рассмотрим теперь случай, когда из уравнения можно явно выразить x, то есть 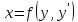. Вводим параметр , получаем . Дифференцируем по y обе части: ; ; ;

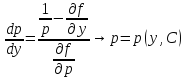
Мы получили уравнение, разрешённое относительно производной . В итоге получаем: .