Лекции + ответы на экзамен (3 семестр) / !Вычеркнутые вопросы и ответы на них

Вопрос 28. Задача Коши для нормальной системы, её геометрический смысл.

Для системы (2) задача Коши ставится так: среди всех решений системы (2) найти такое решение

в котором функции y₁(x), y₂(x), …, y_n(x) принимают заданные числовые значения 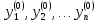при заданном числовом значении x₀ переменной x:

так что решение (3) удовлетворяет условиям:

Здесь числа называются начальными значениями искомых функций или начальными значениями решения (3), число x₀ – начальным значением независимой переменной x; числа вместе взятые называются начальными данными решения (3), а условия (5) – начальными условиями этого решения.

Задачу Коши для системы (2) с начальными условиями (5) геометрически можно формулировать так: среди всех интегральных кривых системы (2) найти ту, которая проходит через заданную точку .

Например, решением задачи Коши для системы с начальными условиями является пара функций и . Геометрически этому решению соответствует интегральная кривая, проходящая через точку (0, 1, -1).

Вопрос 29. Задача Коши для нормальной системы линейных ОДУ, её геометрический смысл.

Задача Коши: среди всех решений системы (1) найти такое решение , которое удовлетворяет условию , . Геометрический смысл задачи Каши заключается в том, чтобы во множестве всех интегральных кривых системы (1) найти ту, которая проходит через точку (

Вопрос 31. Теорема существования фундаментальных систем.

Любое линейное однородное дифференциальное уравнение n -го порядка с непрерывными коэффициентами имеет фундаментальную систему решений, т.е. систему из n линейно независимых решений.

Вопрос 35. Фундаментальная система решений нормальной системы однородных линейных ОДУ с постоянными коэффициентами в случае, когда все корни характеристического уравнения простые, но имеются комплексные корни.

Имеется n неизвестных функций и n уравнений:

Данная система может быть приведена к системе 1го порядка.

После таких преобразований сохранятся только функции и их первые производные. Запишем систему в "нормальном виде":

(*)

Введем матричное обозначение

Тогда – система в векторно-матричном виде.

Решение системы ищем в виде:

- подставляем в (*)

Чтобы система имела решение, отличное от тривиального, необходимо и достаточно, чтобы было корнем уравнения:

– характеристическое уравнение.

- в таком случае называется собственным вектором.

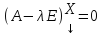
Каждому из корней соответствует хотя бы одно частное решение вида

Рассмотрим случай когда 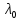- комплексный корень:

Общее решение системы записывается в виде

Вопрос 36. Линейно-зависимые и линейно-независимые системы функций. Необходимое условие линейной зависимости. Теорема об определителе Вронского решений однородного линейного ОДУ.

Рассмотрим m систем функций

Эти системы называются линейно независимыми в интервале (a,b), если не существует чисел a₁, a₂, …, a_m, не равных одновременно нулю, при которых для всего интервала (a,b) выполнялись бы соотношения:

Или

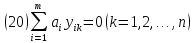
т.е. если никакие линейные комбинации функций каждого столбца таблицы (18), с одними и теми же для всех столбцов постоянными коэффициентами a₁, a₂, …, a_m, не равны нулю в интервале (a,b) или, что то же, если ни одна строка таблицы (18) не является в интервале (a,b) линейной комбинацией всех остальных строк. В противном случае системы (18) называются линейно зависимыми в (a,b).

Очевидно, что если одна из систем функций (18) состоит из функций, тождественно равных нулю в интервале (a,b), то эти системы функций линейно зависимы в (a,b).

Необходимое условие линейной зависимости n систем функций. Пусть мы имеем n систем функций:

Введём в рассмотрение определитель:

Этот определитель называется определителем Вронского для систем функций (3) или вронскианом этих систем функций.

Теорема. Если n систем функций (30) линейно зависимы в интервале (a,b), то в (a,b).

Пусть теперь каждая из систем функции (3) является решением системы (2), так что мы имеем n решений:

Теорема об определителе Вронского решений однородного линейного ОДУ. Если n решений (33) линейно независимы в интервале (a,b), в котором определены и непрерывны p_kl(x), то их вронскиан не обращается в нуль ни в одной точке этого интервала.

Из этой и предыдущей теоремы следует, что для того, чтобы n решений системы (2) были линейно независимы в интервале (a,b), необходимо и достаточно, чтобы их вронскиан не обращался в нуль ни в одной точке этого интервала.

Однако для установления линейной независимости n решений системы (2) достаточно убедиться, что W(x) отличен от нуля хоть в одной точке интервала (a,b). Это вытекает из следующих двух замечательных свойств вронскиана n решений системы (2):

1. Если W(x) обращается в нуль хоть в одной точке интервала (a,b), то есть интервала непрерывности коэффициентов системы (2), то W(x) равен нулю во всех точках этого интервала.

2. Если W(x) не равен нулю хоть в одной точке интервала (a,b), то он не обращается в нуль ни в одной точке интервала (a,b).

Таким образом, для линейной независимости n решений системы (2) в интервале (a,b) необходимо и достаточно, чтобы их вронскиан был отличен от нуля хоть в одной точке этого интервала.

Вопрос 40. Фундаментальная система решений однородного линейного ОДУ с постоянными коэффициентами в случае простых корней характеристического уравнения, действительных или комплексных.

Рассматриваем уравнение , считая в нем коэффициенты . Это уравнение имеет ФСР , определенную для любого x и состоящую из степенных, показательных и тригонометрических функций. Соответствующее ей общее решение .

ФСР ОЛДУ строится по методу Эйлера: частное решение ОЛДУ ищем в виде

где - некоторое постоянное число (вещественное или комплексное), подлежащее определению. Для его определения составляют характеристическое уравнение .

Структура ФСР зависит от вида корней

1. Все корни характеристического уравнения различны и вещественны. ФСР в этом случае имеет вид и общее решение запишется по формуле: .

2. Все корни различны, но среди них имеются комплексные. Пусть - комплексный корень; тогда - тоже корень. Этим двум корням соответствуют два линейно независимых частных решения . Корням в формуле общего решения соответствует выражение вида .

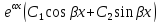3. Среди корней характеристического уравнения имеются кратные корни.

1. Пусть - вещественный k- кратный корень. Тогда ему соответствует k линейно независимых частных решений , а в формуле – выражение вида .

2. Если есть комплексный корень кратности k, то ему и сопряженному с ним корню той же кратности соответствуют 2k линейно независимых частных решений вида В формуле общего решения этим корням соответствует выражение вида .

Вопрос 41. Фундаментальная система решений однородного линейного ОДУ с постоянными коэффициентами в случае, когда имеются кратные корни характеристического уравнения.

– характеристическое уравнение.

Пусть имеется действительный корень λ кратности :

, где P_k1(x) – некоторый многочлен степени r.

Вопрос 43. Теорема существования (локальная) решения задачи Коши для ОДУ первого порядка

См. след. вопрос. Добавление к нему:

Важно понимать, что результат теоремы имеет локальный характер — существование и единственность решения гарантированы, вообще говоря, только в малой окрестности точки x₀ . Важно также понимать, что условия теоремы существования и единственности достаточные условия. Нарушение условий теоремы не означает, что решение задачи не существует либо что оно не единственно.

Вопрос 44. Теорема единственности решения задачи Коши для ОДУ первого порядка.

Рассмотрим обыкновенное дифференциальное уравнение 1–го порядка, записанное в нормальной форме:

. Функция y = y(x) является решением задачи Коши   если y = y(x) дифференцируема на [a,b] , ( для всех x из [a, b] , , и при подстановке в уравнение обращает его в тождество:. Фундаментальным результатом теории обыкновенных дифференциальных уравнений является теорема существования и единственности решения задачи Коши: Если правая часть f(x,y) уравнения и её частная производная по у, то есть , определены и непрерывны в некоторой области D изменения переменных х и у, то какова бы ни была внутренняя точка этой области, данное уравнение имеет единственное решение у=у(х), принимающее при заданное значение . Геометрически это означает, что если условия теоремы выполнены, то через каждую точку области D проходит единственная интегральная кривая уравнения.