19. Принцип дуальності

У законах електричних ланцюгів і описують ланцюга виразах можна виявити подібність співвідношень, записаних для струмів і напруг, зване дуальності: при взаємній заміні струмів і напруг виявляється своєрідна симетрія. Дуальними є пари фізичних величин, топологічних понять і законів ланцюгів, відповідні один одному в дуальних співвідношеннях. Так, індуктивність характеризується компонентним рівнянням u = L di / dt, що зв'язує напругу u і похідну струму di / dt. Дуальним буде рівняння, що виражає струм елемента i через похідну напруги du / dt. Це - зв'язок i = C du / dt для ємності. Звідси випливає, що L і C є дуальними елементами. Також дуальні один одному джерело ЕРС і джерело струму. Дуальні та топологічні поняття контуру і перетину, перший і другий закони Кірхгофа, формулируемого для дуальних один одному топологічних структур. Наведемо деякі основні дуальні величини, поняття і закони (перелік цей може бути продовжений):

контур  розтин; гілки дерева  гілки зв'язків;

паралельне  послідовне з'єднання;

розрив  з'єднання накоротко.

Якщо рівняння для струмів і напруг одного ланцюга тотожні рівнянням для струмів і напруг іншого ланцюга при заміні в них всіх величин на дуальні, такі два ланцюги є дуальними. Вузлам в дуальній ланцюга відповідають елементарні комірки вихідної ланцюга. Дуальними можуть бути тільки планарниє ланцюга.

Принцип дуальності дозволяє поширити результати, отримані при аналізі одних ланцюгів, на дуальні співвідношення в дуальних їм ланцюгах. Для знаходження структури дуальної ланцюга можна скористатися перетворенням рівнянь вихідної ланцюга, замінюючи входять до них величини на дуальні. У найпростіших випадках дуальну ланцюг можна отримати, застосовуючи принцип безпосередньо до топологічних понять і елементів. Так, послідовному з'єднанню джерела й індуктивності в дуальній ланцюга відповідає паралельне з'єднання джерела струму і ємності.

Вузлу 1 вихідної ланцюга (рис. 6.1, а) в дуальній ланцюга (рис. 6.1, б) відповідає елементарний осередок 1, що включає джерело струму J і ємність C _1, дуальну індуктивності L _1.

Рис. 6.1

Вузлу 2 вихідної ланцюга відповідає в дуальній ланцюга осередок 2. Неважко перевірити, що всі топологічні характеристики другій ланцюга (див. рис. 6.1, б) тотожні таким для дуальних величин вихідної ланцюга. Обидві ланцюга описуються і дуальними системами рівнянь:

20. Режим гармонічних коливань. Основні поняття символічного методу.

Режим гармонійних коливань в лінійних ланцюгах.

3.1. ГАРМОНІЧНІ КОЛИВАННЯ

Визначення гармонійного коливання

Електромагнітні процеси в електричному ланцюзі, при яких миттєві значення напруг і струмів повторюються через рівні проміжки часу, називаються періодичними, для їх кількісного опису використовуються періодичні функції часу. Найменший проміжок часу T, після закінчення якого спостерігаються повторення миттєвих значень періодичних функцій a (t) називається періодом:

a (t + T) = a (t).

Величина, зворотна періоду, тобто число періодів в одиницю часу, називається частотою:

f = 1 / T.

Частота має розмірність 1 / с, а одиницею виміру частоти служить герц (Гц).

Переважним видом періодичних процесів в електричних колах є гармонійні коливання, які описуються синусоїдальними або косінусоідальное функціями:

u (t) = Umcos (wt + j);

u (t) = Umsin (wt + y),

де Um - максимальне значення або амплітуда;

w - швидкість зміни аргументу (кута), звана кутовою частотою; вона дорівнює добутку 2pf і вимірюється в радіанах в секунду (рад / с);

j і y - початкові фази, що визначаються зміщенням гармонійних функцій відносно початку координат при t = 0.

Оскільки обидва записи гармонійної функції є еквівалентними при y = j + p / 2, то при аналізі електричних ланцюгів використовують одну. У сьогоденні конспекті буде використовуватися косінусоідальное функція.

Гармонійні коливання володіють важливою властивістю зберігати форму і частоту при перетвореннях в лінійних ланцюгах. Тому вони використовуються при вивченні та описі характеристик лінійних ланцюгів і систем.

Середнє, средневипрямленному і чинне значення гармонійних струмів і напруг

Струми і напруги ланцюга, що змінюються по гармонійному або іншому періодичному закону, поряд з іншими параметрами характеризуються середніми за період, средневипрямленному і діючими значеннями.

Середнє значення періодичної функції a (t) за період 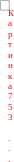визначається виразом

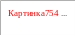(3.1)

Середнє значення гармонійної функції за період дорівнює нулю, так як площа обмежена позитивної напівхвиль і віссю часу, дорівнює площі, обмеженої негативною напівхвиль віссю абсцис.

Средневипрямленному значенням періодичного струму або напруги називається середнє значення модуля відповідної періодичної функції a (t) за період:

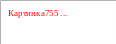(3.2)

Средневипрямленному значення гармонійного струму або напруги дорівнює середньому значенню відповідної гармонійної функції a (t) на позитивному напівперіод.

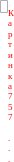Средневипрямленному значення гармонійного коливання одно :

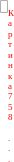Aср.в = (p / 2) Am = 0,637 Am. (3.3)

Діючим значенням періодичної функції a (t) називається середньоквадратичне значення цієї функції за період

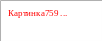(3.4)

Чинне значення A гармонійної функції a (t) в разів менше її амплітуди:

. (3.5)

СИМВОЛІЧНИЙ МЕТОД

Методи розрахунку електричних кіл змінного струму за допомогою векторних діаграм, розглянуті в попередніх розділах, ґрунтуються на зображенні синусоїдних величин векторами.

З курсу математики відомо, що кожному вектору А в комплексній площині (рис. 15.1) відповідає комплексне число А, яке можна подати в формі.

Це дає підставу від графічного (векторного) зображення синусоїдних напруг і струмів перейти до аналітичного вираження їх комплексними числами, а операції з векторами замінити алгебраїчними діями.