
- •1. Основні поняття і закони теорії електричних кіл.
- •2. Лінійні і нелінійні електричні кола з системної точки зору.
- •3. Основні поняття топології електричних кіл.
- •4. Закон Ома для ділянки кола.
- •5. Закони Кірхгофа.
- •6. Пасивні елементи електричного кола.
- •7. Послідовне і паралельне з'єднання елементів кола.
- •10.Метод рівнянь Кіргофа
- •11. Метод контурних струмів.
- •13. Метод двох вузлів.
- •14.Метод накладення
- •15. Метод еквівалентного джерела ерс
- •16. Метод еквівалентного джерела струму.
- •18. Послідовне і паралельне з'єднання нелінійних резисторів.
- •19. Принцип дуальності
- •20. Режим гармонічних коливань. Основні поняття символічного методу.
- •21. Закони електричних кіл в комплексній формі
- •22. Потужність в режимі гармонічних коливань
- •23. Методика розрахунку rc і rl ланок.
- •24. Комплексна функція
- •25. Ачх і фчх електричного кола.
- •26. Логарифмічні частотні характеристики.
- •27. Чутливість електричних кіл.
- •28. Основні схеми включення оп.
- •29. Повітряний трансформатор. Схема заміщення.
- •30. Явище резонансу в нерозгалуженому електричному ланцюзі.
- •34. Що називають амплітудним і фазовим дискретними спектрами? Яким чином будують такі спектри?
- •35. Що називається спектральною щільністю? Приведіть приклади.
- •36. Який сигнал називається дельта-функцією? Розрахуйте його спектральну щільність.
- •37. Суть вейвлет-аналізу
- •38. Сформулюйте умову передачі без спотворення сигналів через електричний ланцюг.
- •39. Що розуміється під апроксимацією вах нелінійних елементів?
- •40. Апроксимація статечними поліномами і кусково-лінійна
- •41. Приведіть схему обмежувача миттєвих значень. Поясніть роботу такого пристрою.
- •42. Покажіть схему випрямляча, поясніть роботу такої схеми.
- •46. Які умови називаються балансом амплітуд і фаз?
- •49. Диференціюючі та інтегруючі ланцюги.
- •50. Що називається прямою передачею, зворотною передачею і зустрічним напрямом передачі? Приведіть приклади.
- •51.Запишіть рівняння чотириполюсників в a-, z-, h- і в y-параметрах. Який фізичний сенс коефіцієнтів чотириполюсників?
- •52.Що називається постійною передачею і робочим ослабленням чотириполюсника?
- •53. Яке включення чотириполюсника називається узгодженим?
- •54. Отримайте еквівалентну п-подібну схему чотириполюсника.
- •56. Телеграфні рівняння для режиму гармонійних коливань
- •57. Що називається падаючою і відображеною хвилями в довгих лініях?
- •58. Що називається фазовою швидкістю? Як вона залежить від довжини хвилі і періоду? Що називається кбв і ксв?
- •59. Виведіть рівняння Хевісайда
40. Апроксимація статечними поліномами і кусково-лінійна
Вона заснована
на використанні добре відомих з курсу
вищої математики рядів Тейлора і
Маклорена і полягає в розкладанні
нелінійної ВАХ
![]() в
нескінченновимірних ряд, що сходиться
в деякій околиці робочої точки
в
нескінченновимірних ряд, що сходиться
в деякій околиці робочої точки
![]() .
Оскільки такий
ряд фізично не реалізуємо, доводиться
обмежувати число членів ряду, виходячи
з необхідної точності. Степенева
апроксимація застосовується при
відносно малій зміні амплітуди впливу
щодо
.
Розглянемо типову форму ВАХ будь-якого
НЕ (рис. 1).
Напруга
визначає положення робочої точки і,
отже, статичний режим роботи НЕ.
.
Оскільки такий
ряд фізично не реалізуємо, доводиться
обмежувати число членів ряду, виходячи
з необхідної точності. Степенева
апроксимація застосовується при
відносно малій зміні амплітуди впливу
щодо
.
Розглянемо типову форму ВАХ будь-якого
НЕ (рис. 1).
Напруга
визначає положення робочої точки і,
отже, статичний режим роботи НЕ.
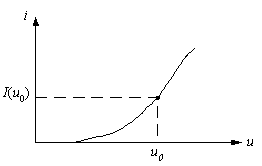 Рис.
1. Приклад типової ВАХ НЕ
Зазвичай
апроксимується не вся характеристика
НЕ, а лише робоча область, розмір якої
визначається амплітудою вхідного
сигналу, а становище на характеристиці
- величиною постійного зміщення
.
Апроксимуючої поліном записується у
вигляді
Рис.
1. Приклад типової ВАХ НЕ
Зазвичай
апроксимується не вся характеристика
НЕ, а лише робоча область, розмір якої
визначається амплітудою вхідного
сигналу, а становище на характеристиці
- величиною постійного зміщення
.
Апроксимуючої поліном записується у
вигляді
![]() ,
(2)
де коефіцієнти
,
(2)
де коефіцієнти
![]() визначаються
виразами
визначаються
виразами
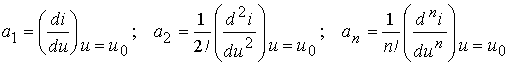 .
Апроксимація статечним поліномом
полягає в знаходженні коефіцієнтів
ряду
.
При заданій формі ВАХ ці коефіцієнти
істотно залежать від вибору робочої
точки
,
А також від ширини використовуваного
ділянки характеристики. У зв'язку з цим
доцільно розглянути деякі найбільш
типові і важливі для практики випадки.
1. Робоча точка розташована на
середині лінійної дільниці (рис. 2).
.
Апроксимація статечним поліномом
полягає в знаходженні коефіцієнтів
ряду
.
При заданій формі ВАХ ці коефіцієнти
істотно залежать від вибору робочої
точки
,
А також від ширини використовуваного
ділянки характеристики. У зв'язку з цим
доцільно розглянути деякі найбільш
типові і важливі для практики випадки.
1. Робоча точка розташована на
середині лінійної дільниці (рис. 2).
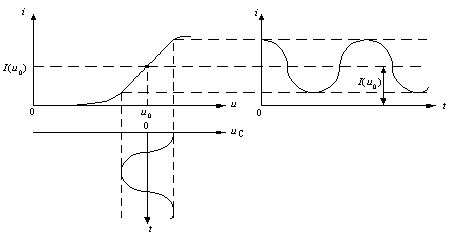 Рис.
2. Робоча точка ВАХ - на середині лінійної
дільниці
Ділянка на характеристиці,
де закон зміни струму близький до
лінійного, щодо неширокий, тому амплітуда
вхідної напруги
Рис.
2. Робоча точка ВАХ - на середині лінійної
дільниці
Ділянка на характеристиці,
де закон зміни струму близький до
лінійного, щодо неширокий, тому амплітуда
вхідної напруги
![]() не
повинна виходити за межі
цієї ділянки. У цьому випадку можна
записати:
не
повинна виходити за межі
цієї ділянки. У цьому випадку можна
записати:
![]() ,
(3)
де
,
(3)
де
![]() -
Струм спокою;
-
Струм спокою;
![]() ;
;
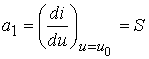 -
Диференційна крутість характеристики.
Цей випадок
застосуємо тільки при слабкому сигналі
-
Диференційна крутість характеристики.
Цей випадок
застосуємо тільки при слабкому сигналі
![]() ,
Оскільки в цьому випадку можна без
великої похибки знехтувати нелінійністю
ВАХ.
2. Робоча точка розташована на
початковому ділянці характеристики.
,
Оскільки в цьому випадку можна без
великої похибки знехтувати нелінійністю
ВАХ.
2. Робоча точка розташована на
початковому ділянці характеристики.
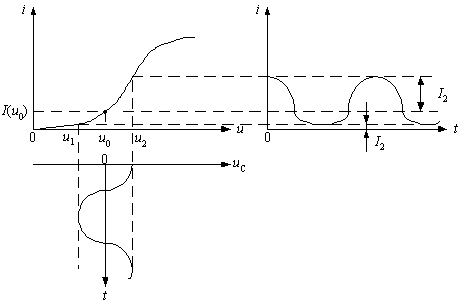
Рис. 3. Робоча точка ВАХ - на початковому ділянці характеристики
При невеликій
зміні амплітуди вхідного сигналу щодо
можна
з малою похибкою апроксимувати ВАХ
квадратичної параболою (статечним
поліномом другого порядку). Апроксимує
вираз матиме вигляд
![]() (4)
Як і у виразі (6.6),
(4)
Як і у виразі (6.6),
![]() -
Струм спокою (постійна складова вихідного
струму);
-
Струм спокою (постійна складова вихідного
струму);
![]() -
Крутизна характеристики в точці
-
Крутизна характеристики в точці
![]() .
Для визначення значень
.
Для визначення значень
![]() і
і
![]() необхідно
скласти систему рівнянь:
необхідно
скласти систему рівнянь:
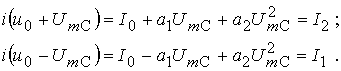 (5)
Звідси можна записати:
(5)
Звідси можна записати:
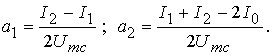 3.
Робоча точка є точкою перегину
характеристики (рис. 4).
3.
Робоча точка є точкою перегину
характеристики (рис. 4).
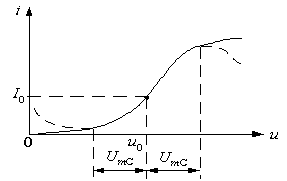
Рис. 4. Робоча точка ВАХ - точка перегину
У точці перегину
всі парні похідні функції
![]() звертаються
в нуль, тому у виразі (3) будуть присутні
тільки доданки з непарними ступенями
звертаються
в нуль, тому у виразі (3) будуть присутні
тільки доданки з непарними ступенями
![]() ,
K
= 1, 2, 3, ....
Нагадаємо, що точка перегину
- точка кривої, у якій:
1) увігнутість
(опуклість) кривої змінюється на
опуклість (увігнутість);
2) крива
"лежить" по різні боки від дотичної
в цій точці.
У загальному випадку
апроксимуючої поліном може бути
будь-якого, скільки завгодно високого
порядку. Однак у більшості практичних
випадків достатню для інженерної
практики точність дає поліном третього
ступеня:
,
K
= 1, 2, 3, ....
Нагадаємо, що точка перегину
- точка кривої, у якій:
1) увігнутість
(опуклість) кривої змінюється на
опуклість (увігнутість);
2) крива
"лежить" по різні боки від дотичної
в цій точці.
У загальному випадку
апроксимуючої поліном може бути
будь-якого, скільки завгодно високого
порядку. Однак у більшості практичних
випадків достатню для інженерної
практики точність дає поліном третього
ступеня:
![]() (6)
На малюнку 4 графік, відповідний
(6), показаний пунктирною лінією. Робоча
ділянка ВАХ (динамічний діапазон)
визначається інтервалом
(6)
На малюнку 4 графік, відповідний
(6), показаний пунктирною лінією. Робоча
ділянка ВАХ (динамічний діапазон)
визначається інтервалом
![]() .
На кордонах цього інтервалу похідні
апроксимуючої функції звертаються в
нуль. Для знаходження коефіцієнтів
і
.
На кордонах цього інтервалу похідні
апроксимуючої функції звертаються в
нуль. Для знаходження коефіцієнтів
і
![]() необхідно,
як і в попередньому випадку, скласти
систему рівнянь і вирішити її відносно
і
:
необхідно,
як і в попередньому випадку, скласти
систему рівнянь і вирішити її відносно
і
:
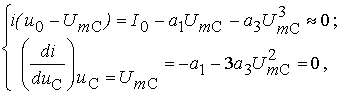 (7)
Звідки
(7)
Звідки
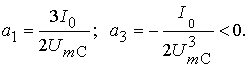 При
дуже великих амплітудах вхідного
сигналу часто буває зручніше замінювати
реальну характеристику ідеалізованої,
складеної з відрізків прямих ліній.
Таке уявлення ВАХ називається
кусково-лінійною апроксимацією. На
малюнку 5 показані деякі характерні
приклади.
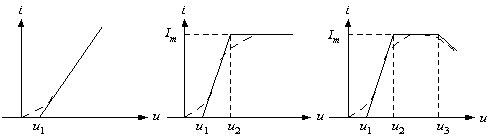
При
дуже великих амплітудах вхідного
сигналу часто буває зручніше замінювати
реальну характеристику ідеалізованої,
складеної з відрізків прямих ліній.
Таке уявлення ВАХ називається
кусково-лінійною апроксимацією. На
малюнку 5 показані деякі характерні
приклади.
 а
б в
а
б в
Рис. 5. Кусково-лінійна апроксимація ВАХ
