2. Расчет сети по временным параметрам (Таблица p-2).

К этому моменту, у вас уже имеется заполненная Таблица Р-1 и сшитый сетевой график. Процесс заполнения таблицы Р-2 состоит из 6 основных этапов:

1. В колонки «i»и «j»заносятся номера (соответственно начальных и конечных) событий для каждой работы по возрастанию номераi, а для работ с одинаковым номеромi– по возрастаниюj. При этом в колонку «работа» заносится буква соответствующей работы (для фиктивных работ ставится прочерк).

2. Для обеих колонок t<i,j>заносится длительность для каждой работы из Таблицы Р-1 (для фиктивных работ она равна 0). Колонкаs²[t_ij] также переносится из Таблицы Р-1 (для фиктивных работ дисперсия равна 0).

3. Для работ, у которых индекс iравен 0, в колонкуt_рн<i,j>заносится 0 (эти работы начинают выполняться сразу и не зависят от других работ). Колонкаt_ро<i,j> для всех работ вычисляется какt_рн<i,j>+ t<i,j>.

Теперь для работ, индекс iу которых равен 1, в качестве значенияt_рн<i,j>выбирается максимальное значениеt_ро<i,j>из строк, индексjв которых равен 1.

Аналогичные действия производятся для всех оставшихся работ.

4. Среди всех значений t_ро<i,j>выбирается максимальное – это и будет величина критического пути.

5. Для работ, у которых индекс jравен номеру последнего события на графике (Nmax), в колонкуt_по<i,j> заносится значение критического пути. Колонкаt_пн<i,j> для всех работ вычисляется какt_по<i,j> –t<i,j>.

Теперь для работ, индекс jу которых равенNmax- 1, в качестве значенияt_по<i,j> выбирается минимальное значениеt_пн<i,j> из строк, индексiв которых равенNmax- 1.

Аналогичные действия производятся для всех оставшихся работ.

6. Значение для всех работ вычисляется по формуле

Как уже упоминалось ранее, полный резерв для работ, лежащих на критическом пути, равен 0. После заполнения таблицы следует отразить критический путь на сетевом графике. Для этого просто подкрашиваются работы, у которых нулевой резерв (фиктивные работы не подкрашиваются). Теоретически, может быть несколько критических путей, но задания подобраны так, что он будет только один.

3. Расчет дополнительных параметров.

Следующие параметры должны записываться в отчет по принципу:

Искомая величина = Формула = Результат

с опусканием 2 составляющей там, где это возможно.

Значение критического времени, далееT_КР.

T_дир Директивный срок выполнения комплекса работ. Это округленное до десятковT_КРс округлением в большую сторону. (T_дир(123) = 120;T_дир(135) = 140).

Дисперсия критического пути (сумма дисперсий работ критического пути).

Квадратный корень из дисперсии критического пути.

Временной интервал, в которыйT_КРпопадает с

вероятностью 99.8% (вычисляется по правилу трех сигм).

Вероятность того, что критическое время окажется

меньше T_дир. Берется из Таблицы 3 нормального распределения от рассчитанного параметраx.

Работа с минимальным ненулевым резервом (надкритическая работа) заключается в скобки < x , y >, где указывается пара номеров начального (x) и конечного (y) событий этой работы. Если таких работ несколько, то выбирается работа с наибольшей дисперсией.

В последующих выражениях обозначает резерв.

Величина полного резерва выбранной работы.

Величина раннего резерва выбранной работы.

Величина позднего резерва выбранной работы.

Величина независимого резерва выбранной работы.

Дисперсия полного резерва, вычисляется по формуле:

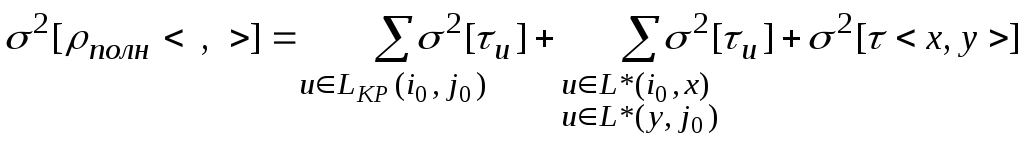
На сетевом графике это выглядит следующим образом:

Вначале для работы с минимальным ненулевым резервом < x , y >определяется путь максимальной длительности, проходящий через нее. Затем выделяется первая общая вершинаi₀путейL^*(I, x)иL_КРи последняя общая вершина путейL^*(y, C)иL_КР- вершинаj₀. Жирными линиями на графике обозначен критический путь, нежирными - .

Расчет вероятности того, что путь, проходящий через работу с минимальным, отличным от нуля полным резервом, будет длиннее критического пути.

Вероятность берется из Таблицы 3 нормального распределения от рассчитанного параметра x.