22.Шероховатость….
Шероховатость поверхности — совокупность неровностей поверхности с относительно малыми шагами на базовой длине. Измеряется в микрометрах (мкм). Шероховатость относится к микрогеометрии твёрдого тела и определяет его важнейшие эксплуатационные свойства. Прежде всего износостойкость от истирания, прочность, плотность (герметичность) соединений, химическая стойкость, внешний вид. В зависимости от условий работы поверхности назначается параметр шероховатости при проектировании деталей машин, также существует связь между предельным отклонением размера и шероховатостью. Исходная шероховатость является следствием технологической обработки поверхности материала, например, абразивами. В результате трения и изнашивания параметры исходной шероховатости, как правило, меняются.
Если высота выступов шероховатости Δ меньше, чем толщина ламинарной пленки (Δ <δ), то в этом случае шероховатость стенок не влияет на характер движения и соответственно потери напора не зависят от шероховатости, а стенки называются гидравлически гладкими.
Когда высота выступов шероховатости превышает толщину ламинарной пленки (Δ <δ), то потери напора зависят от шероховатости, и такие трубы называются гидравлически шероховатыми. В третьем случае, являющемся промежуточным между двумя вышеуказанными, абсолютная высота выступов шероховатости примерно равна толщине ламинарной пленки. В этом случае трубы относятся к переходной области сопротивления. Толщина ламинарной пленки определяется по формуле:
Эквивалентная шероховатость - такая условная, постоянная по длине трубы шероховатость, образованная выступами одинаковой высоты еа, при которой потери энергии потока на трение будут теми же самыми, что и при данной реальной шероховатости с выступами различной величины.
23.Графики Никурадзе и Мурина
Наиболее полные исследования по определению зависимости коэффициента l от числа Рейнольдса и от относительной шероховатости были выполнены И. Никурадзе.
И.
Никурадзе испытал ряд труб с искусственно
созданной шероховатостью на их внутренней
поверхности. Шероховатость была получена
путем приклейки песчинок определенного
размера, полученных просеиванием через
сита. Такая шероховатость называется
равномерно зернистой. Испытания были
проведены при широком диапазоне
относительных шероховатостей
,
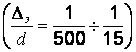а также чисел Рейнольдса
.
Данные опытов И. Никурадзе изобразил на графике, где по оси абсцисс откладывались логарифмы величин Re, а по оси ординат – логарифмы 100 l при различных значениях относительных шероховатостей (рис. 6.6).
Рис. 6.6. График Никурадзе
При Re < 2300 (lgRe < 3,36) – прямая 1 – имеет место ламинарный режим и l зависит только от числа Рейнольдса и не зависит от шероховатости стенок.
При
– участок 2
– наблюдается быстрый переход от
ламинарного режима к турбулентному.
Далее начинается прямая 3,
характеризующая зависимость l
от числа Рейнольдса для гидравлически
«гладких» труб, у которых величина
выступов шероховатостей меньше толщины
ламинарной пристенной пленки. Далее
кривые зависимости l
от Re
расходятся. Участки кривых 4
характеризуют собой переход от
гидравлически «гладких» труб к
гидравлически «шероховатым» трубам 5,
т. е. в зоне 4–5
коэффициент гидравлического трения l
зависит как от шероховатости, так и от
Re.
Последняя область 5 представлена линиями, параллельными оси абсцисс, что свидетельствует о том, что здесь коэффициент гидравлического трения зависит только от шероховатости. Эту область обычно называют областью квадратичного сопротивления, так как потери напора по длине пропорциональны квадрату скорости.
Для труб с естественной шероховатостью закон изменения l от Re получается несколько иным, без подъема кривых после отклонения их от линии гладких труб. Различие объясняется тем, что в трубах с естественной шероховатостью выступы шероховатости имеют различную высоту и при увеличении числа Рейнольдса начинают выступать за пределы ламинарного слоя не одновременно, а при разных Re. Поэтому переход от линии «гладких» труб к горизонтальным прямым, соответствующим квадратичному закону, происходит более плавно, без провала кривых, что наглядно представлено на графике Г. А. Мурина (рис. 6.7).
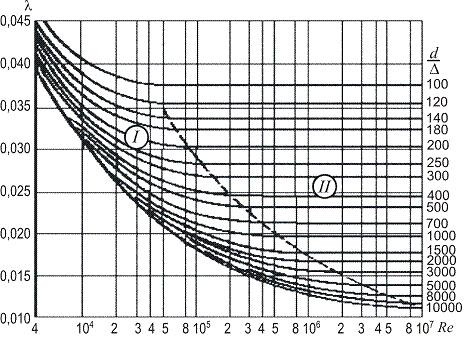
Рис. 6.7. График Мурина