Формальное описание риска

А) Со стратегией связано множество неблагоприятных событий

,

Пусть у стороны А имеется n возможных стратегий:

и с каждой принимаемой стратегией связано множество неблагоприятных событий

с условными вероятностями , ,

Каждому сочетанию и поставлено в соответствие количественное описание последствия , тогда величина, сопутствующая риска определяется как сумма

– средняя величина ущерба при принятии решения

Б) Пусть с некоторым рискованным вариантом решения связаны всевозможные сочетания неблагоприятных событий

,

и каждому мысленному сочетанию неблагоприятных событий , которое может реализоваться в результате принятия решений можно приписать условную вероятность , и количественно описываемое последствие, тогда величина риска сопутствующего решению определяется формулой:

Пусть – полезность варианта решения без учета возможных неблагоприятных последствий, тогда соответствующая варианту решения величина – суммарный эффект решения.

Вариант решения называется оптимальным, если он

При этом в рамках конкретной практической задачи множество допустимых вариантов решения может быть дополнительно ограничено пределами риска.

Если выигрыш определен, то риск при использовании стратегии и неблагоприятном событии определяется выражением

,

То есть риском лица, принимающего решение при использовании стратегии в условиях , называется разность между выигрышем, который он получил, если бы знал , и выигрышем, который он получит в тех же условиях, принимая стратегию

Матрица рисков дает более наглядную картину, чем матрица выигрыша.

	1	4	5	9
	3	8	4	3
	4	6	6	2

	3	14	1	0
	1	0	2	6
	0	2	0	7

Стратегия, максимизирующая средний выигрыш, совпадает со стратегией, минимизирующей средний риск.

Тогда

То есть величина обращается в минимум, когда в максимум.

Планирование эксперимента в условиях природной неопределенности

Задача: предстоит провести некоторую операцию в недостаточно выясненных условиях. Имеет ли смысл для уточнения условий в нашей неопределенной ситуации применять эксперимент для уточнения условий операции?

Этот вопрос возникает, когда затраты существенны и сравнимы с тем увеличением выигрыша, который мы можем получить, узнав обстановку более точно.

Пусть затраты на проведение эксперимента равны . Сравним средний выигрыш без/с проведением эксперимента.

Без: максимальный средний выигрыш

С: средний выигрыш

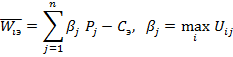
Эксперимент целесообразен, если максимальный средний выигрыш

Эксперимент следует проводить, если затраты на его осуществление меньше минимального среднего риска.

Задача:

	1	2	3
1	1	2	-1	0.4
2	0	-1	1	1.4
3	-1	0	-2	2.2
	1	2	1	0.4