
- •Преобразование структуры проектируемых систем
- •Декомпозиция процесса р
- •Координируемость
- •Координируемость по отношению к задаче, решаемой вышестоящей управляющей системой.
- •Координируемость по отношению к глобальной задаче.
- •Принципы координации
- •Описание взаимодействия структурных элементов системы.
- •Классификация задач оптимизации и задач принятия решений.
- •Бинарные отношения
- •Способы задания бинарных отношений.
- •Принятие решений в условиях природной неопределенности
- •Формальное описание риска
- •Планирование эксперимента в условиях природной неопределенности
- •Классические критерии принятия решений в условиях неопределенности
- •Расширенный минимаксный критерий
- •Методы решения задач векторной (многокритериальной) оптимизации.
- •Методы поиска компромиссных решений в задачах векторной оптимизации.
- •Пример экспертизы проекта ла методом маи
Классификация задач оптимизации и задач принятия решений.
Классификация задач оптимизации.
Постановка любой задачи оптимизации предполагает наличие следующих обязательных компонентов:
Математическая модель объекта оптимизации
Область определения и существования моделей
Критерий оптимальности или ЦФ.
По характеру объекта оптимизации и соответственно по характеру искомого решения различают статические и динамические задачи оптимизации.
К первым относятся задачи оптимизации так называемых статических объектов, математические модели которых могут быть представлены в виде некоторых зависимостей ЦФ от искомых параметров.
Такие задачи называют задачами математического программирования.
Для статических задач оптимизации формализованная модель принятия решения имеет вид: максимизировать или минимизировать функцию при ограничениях:
![]()
![]()
![]() (показатель
качества) системы
(показатель
качества) системы
- вектор управляющих переменных;
![]() - вектор неуправляемых переменных;
- вектор неуправляемых переменных;
![]() – функция потребления -го ресурса;
– функция потребления -го ресурса;
![]() - величина -го ресурса.
- величина -го ресурса.
Для нахождения оптимальных значений задачи в зависимости от вида и структуры ЦФ и функций ограничения используют следующие методы оптимизации:
Класс задачи безусловной оптимизации
Линейное программирование (может быть применено в случаях, где функции
 и
и  линейны относительно переменной
)
линейны относительно переменной
)Нелинейное программирование (если и нелинейны относительно переменных)
Динамическое программирование (если ЦФ имеет специальную структуру, являясь аддитивной или мультипликативной функцией от переменных )
![]() аддитивная, если:
аддитивная, если:
![]()
![]() – мультипликативная, если:
– мультипликативная, если:
![]()
Геометрическое программирование (если ЦФ и ограничения
 имеют название – функции-позиномы)
имеют название – функции-позиномы)
![]() - позином
- позином
Математическая модель задачи в этом случае записывается в следующем виде: максимизировать и минимизировать функцию следующего вида:
![]()
при условиях, что функция
![]()
![]()
Пример: связь 111 подсистемы; использовать геометрическое программирование позином.
Стохастическое программирование
Математическая модель задачи будет иметь следующий вид:
![]()
при ограничениях вида:
![]()
или вероятностных ограничениях
![]()
![]() - какая-то пороговая величина (доверительная
вероятность)
- какая-то пороговая величина (доверительная
вероятность)
![]() - математическое ожидание по Y
- математическое ожидание по Y
Вероятность выполнения
условия ![]() :
:
![]()
Дискретное программирование (если на переменные налагается условие дискретизации, например, целочисленности)
Используется при решении задач целераспределения, есть цели, есть носители, средства поражения на них, нужно распределить их по целям.
Эвристическое программирование (в силу сложности задачи используются специальные приемы, эвристики, позволяющие существенно сократить число просматриваемых вариантов)
Методы многокритериальной оптимизации (в этом случае критериальная функция является векторной и включает набор ЦФ) Решение данной задачи состоит в определении множества Парето или неулучшаемых решений, из которых в последействии выбирается единственное.
Методы принятия решения при нечеткой исходящей информации. Они позволяют формализовать нечеткие понятия и суждения, которыми оперирует человек при описании своих представлений о желаемых целях и системе.
Вторую группу методов составляют задачи оптимизации управления динамическими системами.
Как правило, математические модели таких объектов представляют систему дифференциальных уравнений или разностных уравнений.
Условием оптимальности в такой задаче служит некоторый функционал, устанавливающий связь искомого управления с ЦФ через систему дифференциальных или разностных уравнений.
В современной теории управления такие задачи принято называть задачами оптимального управления.
Конкретная задача оптимального управления определяется типом уравнений, описывающих эволюцию системы видом минимального функционала и ограничениями на траекторию и управление.
В зависимости от характера исследуемой задачи для ее описания можно использовать объектные дифференциальные уравнения, разностные уравнения, стохастические уравнения и т.д. В зависимости от способа задания минимального функционала принято различать задачи Майера, Лагранжа, Больца.
В задаче Лагранжа критерий качества:

![]() - заданная скалярная функция;
- заданная скалярная функция;
![]() - момент окончания движения.
- момент окончания движения.
Если ![]() ,
то задача, состоящая в минимизации
времени управления, называется задачей
быстродействия.
,
то задача, состоящая в минимизации
времени управления, называется задачей
быстродействия.
Пример:
Максимизировать
дальность полета ракеты при заданных
ограничениях из т.1 в т.2, минимизируя
время полета ![]() .
.

В задаче Майера критерий качества зависит от траектории системы в момент Т окончания движения.
![]()
В задаче Больца:

В ряде случаев целеуправления является стабилизация задач программирования движения.
Для этой задачи часто используется квадратичная функция вида:

![]() (управление определяется аналитически)
(управление определяется аналитически)
![]() неотрицательно определены
неотрицательно определены
Классификация задач принятия решений.
Любой процесс принятия решений характеризуется следующими элементами:
Лицо, принимающее решение (ЛПР), которое должно нести ответственность за последствия этих решений.
Множество переменных, зависящих от выбора стратегии. Их будем называть исходами или результатами решений.
Множество переменных, значения которых выбираются ЛПР. Будем называть их стратегиями.
Множество переменных, значения которых не регулируются ЛПР. Эти переменные могут остаться вполне определенными при решении задачи и тогда их называют параметрами задачи. Иначе они могут изменяться независимо от ЛПР и тогда это возмущения.
Интервал времени, на котором принимается решение в рассмотренной системе.
Математическая модель, связывающая стратегии и параметры задачи с исходами решений.
Определения, отображающие требования, налагаемые ситуацией принятия решений на исходы решений и стратегии.
ЦФ или критерий оптимизации, с помощью которого оцениваются свойства выбираемого решения. При этом ЦФ должна зависеть от стратегий согласно математической модели задачи принятия решений.
В зависимости от условий внешней среды и степени информированности ЛПР существуют следующие классификации задач принятия решений.
В условиях определенности каждая стратегия приводит к одному исходу
В условиях неопределенности, которая включает следующие варианты:
Условия природной неопределенности: стратегия приводит к нескольким исходам, появление каждого из которых связывается с определенной вероятностью;
В условиях неопределенности целей и задач проекта: это так называемые задачи многокритериального выбора;
В условиях конфликтной неопределенности: исход зависит от стратегий, выбираемых противником.
При нечетко сформированных целях и ограничениях: описания цели проектирования и ограничений проводятся аппаратом теории нечетких множеств.
Принятие решений в условиях определенности.
Функция полезности и бинарные соединения.
Принятие решений в условиях определенности характеризуется однозначной детерминированной связью между принятым решением и его исходом.
Рассмотрим проблему выбора решений в условиях определенности. Совокупность стратегий, удовлетворяющих ограничениям, - множество альтернатив А.
Для сравнения альтернатив и выбора лучшей из них используется функция полезности. Применение теории полезности основывается на следующих аксиомах:
Альтернатива
 предпочтительней альтернативы
предпочтительней альтернативы  :
:
![]()
![]() - полезности альтернатив
- полезности альтернатив ![]()
Если
 ,
,
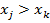 ,
то
,
то  и
и  (свойство транзитивности)
(свойство транзитивности)Если некоторый результат можно представить в виде
 ,
то
,
то 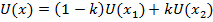 (свойство линейности)
(свойство линейности)Если U
 - полезность от достижения и одновременно
функция полезности результатов
- полезность от достижения и одновременно
функция полезности результатов  и
,
то свойство аддитивности функции
записывается как
и
,
то свойство аддитивности функции
записывается как
U![]()
Аналогично, если
имеется ![]() ,
то функция полезности от достижения
одновременно этих результатов определяется
как
,
то функция полезности от достижения
одновременно этих результатов определяется
как
U![]()
Определим в терминах
функции полезности ![]() следующее отношение на множестве
альтернатив А:
следующее отношение на множестве
альтернатив А:
Отношение слабого предпочтения

Отношение равноценности
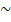
Отношение строгого предпочтения

Для двух альтернатив
и
будем говорить, что ![]() тогда и только тогда, когда
тогда и только тогда, когда ![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() при сравнении значений функции полезности
для различных альтернатив берутся в
зависимости от того, считается ли лучше
альтернатива при большем или меньшем
значении функции полезности.
при сравнении значений функции полезности
для различных альтернатив берутся в
зависимости от того, считается ли лучше
альтернатива при большем или меньшем
значении функции полезности.
Рассмотрим несколько вариантов методики определения функции полезности:
Имеется два результата. Определяем, какой результат предпочтительнее для ЛПЛ

Определяем такую вероятность 𝜶, при которой достижение результатов будет эквивалентно результату , получаемому с вероятностью 1
Оцениваем соотношения между полезностями результатов и , для этого принимаем:
Значение полезности при
 ,
тогда
,
тогда 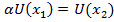 :
:

Имеется n возможных результатов, между которыми установлено отношение предпочтения:
![]()
1 шаг:
Определяем величину ![]() из следующих отношений:
из следующих отношений:
![]()
![]()
…
![]()
2 шаг: Положив полезность наименее предпочтимого результата:
![]()
![]()
…
![]()
Некоторые критерии являются качественными.
Имеется n результатов:
![]()
Выполняем следующие действия:
Упорядочим все результаты по убыванию предпочтительности: пусть наиболее предпочтительный результат, а
 наименее.
наименее.Составляем таблицу возможных комбинаций результатов, достигаемых одновременно, и затем устанавливаем их предпочтительность относительно их результатов.
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
|
|
|
|
n |
|
|
|
3 шаг: Приписываем начальные оценки полезности одинаковых результатов
![]()
Если ![]() удовлетворяет заданным начальным
условиям, то начальные значения не
изменяют. В противном случае производят
коррекцию полезностей так, чтобы
удовлетворить данное соотношение.
Переходят к следующему от конца
соотношению. Процесс коррекции
продолжается до тех пор, пока не образуется
система оценок
удовлетворяет заданным начальным
условиям, то начальные значения не
изменяют. В противном случае производят
коррекцию полезностей так, чтобы
удовлетворить данное соотношение.
Переходят к следующему от конца
соотношению. Процесс коррекции
продолжается до тех пор, пока не образуется
система оценок
![]() ,
которая будет удовлетворять всем
соотношениям.
,
которая будет удовлетворять всем
соотношениям.
Коррекцию следует производить таким образом, чтобы изменять по возможности оценки для минимального количества результатов.
