Основные понятия, определения и принципы системного анализа

Системный анализ – базовая дисциплина, объединяющая методы исследования систем.

Понятие системы. Классификация систем.

Система существует среди других объектов, объединенных понятием внешняя среда. Объекты внешней среды связаны с системой и ее компонентами. Понятие системы относительное, зависящее от цели и объекта исследования. Выявление системы есть разделение некоторой области материального мира на 2 части: одна из которых рассматривается как система (т.е. объект исследования или изучения), а другая – как внешняя среда.

Под системой будем понимать отграниченный в окружающей ее внешней среде и взаимодействующий с внешней средой объект, который обладает следующими свойствами:

1)имеет цель, для достижения которой он существует;

2)состоит из взаимосвязанных составных частей (компонентов), образующих многоуровневую иерархическую структуру и выполняющих определенные функции, направленные на достижение цели объекта;

3)имеет управление, благодаря которому все компоненты функционируют согласованно и целенаправленно.

4)имеет в своем составе или во внешней среде источники энергии и материалов для функционирования.

5)обладает свойствами, не сводимыми к сумме свойств ее компонентов.

Система в процессе проектирования представляет собой виртуальную модель будущей реальной системы. Виртуальная модель может быть представлена четверкой следующих множеств:

, где

- виртуальная модель,

- множество, элементы которого дают информацию о фактах внешней среды, действующей на систему;

- множество, дающее информацию о подсистемах и элементах проектируемой системы;

- множество, элементы которого есть информация об отношениях между компонентами проектируемой системы, а также об отношениях между системой с ее составляющими и внешней средой;

- множество, элементы которого несут информацию о качествах системы, определяемых факторами внешней среды, компонентами системы и отношениями между компонентами системы, а также между системой и внешней средой.

По сложности системы подразделяются на элементарные (простые) и сложные.

Простые системы являются совокупностью конечного числа объектов, объединенных для решения простейших или единичных задач. Отличительная особенность этих систем – это полная детерминированность номенклатуры и числа элементов и связи внутри системы, а также связи системы с внешней средой.

Система имеет вход и выход. На вход подаются воздействие внешней среды и управление, с помощью обратной связи и ограничений влияющее на ее характеристики и поведение.

Выход системы – совокупность воздействий системы на внешнюю среду.

Обратная связь – это связь, определяющая влияние выхода системы на вход.

Управление – это целенаправленное воздействие на вход системы с целью влияния на ее выход.

Движение системы – это процесс последовательных смен состояний системы в пространстве и во времени.

Наиболее общая классификация систем предусматривает их деление на два основных вида: абстрактные и материальные.

Материальные системы являются объектами реального мира, которые в свою очередь делятся на естественные и искусственные. Естественные системы представляют собой совокупность объектов природы, а искусственные – совокупность технических и социально-экономических объектов.

Искусственные системы могут быть классифицированы по нескольким признакам, в т.ч. и по роли человека в системе. По этому признаку можно выделить технические, эргономические и организационно-эргономические системы.

В основе функционирования технических систем лежат процессы, совершаемые машинами, роль человека при этом незначительна. В эргономических системах рассматриваются человеко-машинные комплексы. В основе организационно-эргономических систем доминирующим является поведение человека.

Абстрактные системы – это виртуальное представление образа или модели материальных систем, которые подразделяются на логические (описательные) и символические (математические).

Логические системы могут рассматриваться как системы понятий и определений о структуре основных закономерностях состояний и о динамике материальных систем.

Символические системы представляют собой математическую формализацию логических систем.

Сложная техническая система (СТС) – это совокупность технических и эргономических систем, объединенных выполнением комплексных задач, взаимодействующих друг с другом и внешней средой в ходе функционирования и выступающих по отношению к внешней среде как единое целое для достижения общей для них цели.

Их отличительной чертой является недетерминированность связи как внутри системы, так и во взаимодействии с внешней средой.

Внешнюю среду, взаимодействующую с СТС целесообразно разбить на 3 группы:

1)противодействующую, т.е. порождаемую разумно действующим противником;

2)сотрудничающую, т.е. порождаемую сотрудничающими системами;

3)физическую среду, в которой функционирует СТС.

СТС определяется обликом и поведением.

Облик СТС задается структурой и конструктивными параметрами.

Структура системы характеризует тип, состав и компоновку (т.е. взаимное расположение) основных компонентов СТС.

Конструктивные параметры определяют конструкцию СТС и ее компоненты количественно.

Поведение – это развернутое во времени последовательность реакций СТС на внешнее воздействие.

СТС обладает целенаправленным поведением и стремится достигнуть определенного предпочтительного для них состояния, которое является их целью.

Цель – это желаемый результат деятельности, достижимый в пределах некоторого интервала времени.

В основном СТС являются многоцелевыми.

При количественной конкретизации цели, она становится задачей.

Задача – это желаемый результат деятельности, достижимых за заданный интервал времени и характеризуется конкретным набором параметров этого результата.

Совокупность мероприятий, организуемых для выполнения поставленной задачи является операцией.

Операции протекают с использованием средств, которые называют ресурсами, а способ проведения операции – стратегией.

Операции, проводимые СТС оцениваются степенью ее приспособленности к выполнению функций и задач, для которых она предназначена.

Эта степень приспособленности называется эффективностью СТС. Количественно мера эффективности СТС называется показатель эффективности применения СТС в выполнении операции.

Различают общие и частные показатели эффективности.

Общие определяют эффективность операции в целом, а

частные – эффективность отдельных этапов и фрагментов операции.

СТС состоит из составляющих частей (компонентов).

Компоненты системы могут быть двух типов: подсистемы и элементы.

Под элементом понимается простейшая для данной задачи неделимая часть СТС, выполняющая в ней определенные функции, т.е. в условиях рассмотрения задачи они не подлежат дальнейшему членению.

Подсистемы же расчленяются дальше на свои компоненты: системы более низкого ранга и элементы.

Каждая подсистема может рассматриваться как система более низкого уровня, а сама исследуемая система может входить составной частью (компонентом) в некоторую систему более высокого уровня.

Совокупность составляющих систему компонентов в их взаимодействии друг с другом представляют собой структуру системы.

Связи между компонентами системы называются структурными.

В общем случае можно выделить 2 основных типа структурных связей: подчинение подчиненностей (вертикальные связи между компонентами разных иерархических уровней), согласование (связи между компонентами, находящимися на одном иерархическом уровне – горизонтальные связи).

Тип связи между компонентами определяет иерархическую структуру системы, т.е. размещение компонентов системы по иерархическим уровням.

Между компонентами системы и компонентами внешней среды возникают коммуникативные связи.

Иерархической структуре системы можно поставить в соответствие иерархическую структуру функций компонентов.

На верхнем уровне этой структуры находится цель системы, на достижение которой направлены функции компонентов.

Функции компонентов можно трактовать как цели функционирования компонентов.

В основе методов системного анализа лежит системный подход.

Системный подход – это подход к исследованию СТС, при котором свойства СТС определяются не только свойствами ее компонентов, а существенным образом зависят от их взаимодействия между собой и окружающей внешней средой.

Основные принципы системного подхода состоят в следующем:

1) принцип целостности, говорящий о принципиальной несводимости свойств СТС к сумме свойств ее компонентов и несводимости из последних свойств целого;

2) принцип структурности, предполагающий, что если один из компонентов СТС будет заменен другим адекватно взаимодействующим, то структура системы не изменится;

3) принцип иерархичности, согласно которому каждый компонент системы в свою очередь может рассматриваться как система, а исследуемая в данном случае система представлять собой один из компонентов более общей системы.

Это обстоятельство допускает декомпозицию системы и возможность отдельного проведения исследования ее компонентов.

Декомпозицией называют процесс разбиения системы на уровни иерархии и подсистемы на каждом иерархическом уровне с выделением существенных связей между ними, общих (глобальных) и частных показателей эффективности системы и ее подсистем, подчиненных достижению общей цели.

Пример.

Декомпозиция системы ПВО для проектирования зенитно-ракетной системы.

1.1 – Зенитный ракетный комплекс малой дальности;

1.2 - Зенитный ракетный комплекс средней дальности;

1.3 - Зенитный ракетный комплекс большой дальности;

1.4 – Средства неогневой защиты;

1.5 – Пункты боевого управления;

1.6 – Информационные средства дальнего обнаружения;

1.7 – Средства радиотехнической разведки;

1.1.1 – Информационные средства обнаружения;

1.1.2 - Информационные средства наведения;

1.1.3 – Пусковая установка;

1.1.4 – Боекомплект зенитных управляемых ракет (ЗУР);

1.1.5 – Система электропитания;

1.1.6 – Электронная вычислительная машина;

1.1.7 – Самоходная установка;

1.1.8 – Дополнительное оборудование;

1.1.4.1 – Система управления ЗУР;

1.1.4.2 – Система стабилизации ЗУР;

1.1.4.3 – Боевая часть;

1.1.4.4 – Взрыватель;

1.1.4.5 – Двигательная установка;

1.1.4.6 – Корпус ЗУР;

1.1.4.7 – Крылья;

1.1.4.8 – Рули стабилизации;

1.1.4.9 – Ускоритель ракета.

Иерархия показателей эффективности и затрат в задаче оптимального проектирования зенитного вооружения.

уровни иерархии	показатели
	эффективности	затрат
n (ЗРС)	Мера предотвращенного зенитной ракетной системой ущерба: где i – тип ЗРК; k – тип СВН; m – количество типов ЗРК в ЗРС; - число пораженных i-ым типом ЗРК средств воздушного нападения (СВН); - неизрасходованный боевой потенциал СВН k-ого типа по обороняемым объектам.	Затраты ЗРС на операцию: где - число боевых машин в составе i-го типа ЗРК; - число ЗРК i-го типа в составе ЗРК; - суммарное число боевых машин остальных средств ЗРС.
n-1	Мера предотвращенного ЗРК ущерба: или - вероятности выживания ЗРК в налете; Т – чисто налетов СВН в операции.	Затраты ЗРК на операцию: где J – число подсистем в составе ЗРК; - масса j-ой подсистемы ЗРК.
n-2	Тактико-технические характеристики (ТТХ) ЗУР хj (где j – индекс подсистемы): 1) вероятность поражения различных типов целей по зоне поражения; 2) размеры зоны поражения; 3) средняя скорость полета ЗУР по зоне поражения; …	Стартовая масса ЗУР:

Обратная декомпозиции процедура называется агрегированием.

Агрегирование – это процедура, при которой группа подсистем, входящие в состав СТС, заменяется новым компонентом таким образом, что отношение связывающее вводимый компонент с другими компонентами СТС и внешней средой совпадает с внешними отношениями агрегируемой группы.

4) принцип взаимозависимости системы и внешней среды: система формирует и проявляет свои свойства в процессе взаимодействия со средой.

5) принцип множественности описания каждой системы, т.е. при исследовании системы, в силу ее сложности, требуется построение различных моделей для данной системы, каждая из которых описывает лишь определенный аспект системы.

Системный анализ предполагает изучение СТС с различных аспектов, основными из которых являются:

1) системно-компонентный (из каких компонентов образована система);

2) системно структурный (организация внутренней структуры и способ взаимодействия образующих ее компонентов);

3) системно-функциональный (какие функции выполняет система и образующие ее компоненты);

4) системно-коммуникационный (взаимосвязь данной системы с внешней средой);

5) системно-временнóй (определяет жизненный цикл системы);

6) системно-интегративный (определяет механизмы и факторы сохранения и развития системы);

7) системно-исторический (это обстоятельства возникновения системы, этапы развития и исторические перспективы);

Методы системного анализа включают

разработку общей схемы решения поставленной проблемы и основных ее этапов;

способы формирования целей и задач;

назначение и согласование критериев (показателей эффективности);

декомпозицию системы и операции ее разработки и применения;

методические основы формирования альтернатив и общую методологию подготовки обоснованных решений.

Основное содержание системного анализа, применительно к задачам исследования авиационных боевых комплексов и комплексов их вооружения (АБК и КАВ).

Первым шагом при исследовании АБК и КАВ является представление их в виде иерархических структур по функциональному признаку.

Под АБК будем понимать совокупность ЛА, его бортовых систем, экипажа (в пилотируемых – пилот, в беспилотных – оператор), систем управления боевыми действиями, средств инжененрно-аэродромного и аэродромно-технического обеспечения, предназначенных для выполнения некоторого множества боевых задач.

Схема:

Комплекс авиационного вооружения (КАВ) представляет подсистему АБК и предназначен для обеспечения доставки, атаки и поражения наземных, морских и воздушных целей противника.

КАВ состоит из следующих систем:

1) прицельно-навигационного комплекса, обеспечивающего обнаружение цели, выход в атаку и прицеливание;

2) установок вооружения, предназначенных для транспортировки и отделения средств поражения;

3) системы управления вооружением, управляющей процессом применения АБК и средств поражения и самих авиационных средств поражения, предназначенных для непосредственного поражения цели.

КАВ обеспечивает выполнение основных этапов боевого вылета, наведение на цель, ее атаку с применением АСП.

В свою очередь АБК является составной частью авиационной системы оружия, под которой будем понимать совокупность функционально связанных между собой АБК, авиационных комплексов обеспечения боевых действий, включающих заправщики, ретрансляторы, самолеты радиоэлектронной борьбы, спутниковые группировки.

Авиационные системы боевого управления, которые включают

1) наземные и воздушные пункты наведения систем аэродромного и инженерного обслуживания;

2) совокупность АБК вместе с соответствующими системами управления и обеспечения боевых действий определенным образом расположенными на театре военных действий (ТВД) образуют группировку авиации на ТВД.

Из всей группировки могут быть выделены группировки рода авиации (истребительная, ударная,…).

АБК и КАВ принято называть СТС и их исследования проводятся на основе методологии системного анализа.

КАВ является подсистемой АБК. Следовательно, цели, задачи и показатели эффективности КАВ должны непосредственно следовать из цели, задач и показателей эффективности АБК, а те в свою очередь из целей, задач и показателей эффективности группировки рода авиации.

Чтобы иметь возможность анализировать влияние характеристик КАВ на эффективность АБК необходимо сформулировать цели и определить показатели эффективности АБК и группировки данного рода авиации.

Выход за рамки собственно КАВ при анализе его эффективности необходим еще и потому, что некоторые и свойств КАВ проявляют себя на уровне АБК и группировки и их невозможно оценить оставаясь на уровне КАВ.

С другой стороны КАВ является подсистемой АБК, представляет СТС, состоящую из ряда подсистем, показатели эффективности которых следуют из показателей следуют из показателей эффективности АБК.

Практическая необходимость изучения АБК на соответствующем уровне иерархии определяется теми параметрами или способами боевого применения, которые подлежат исследованию.

Уровень иерархии, который необходимо рассматривать является необходимым, если хотя бы один из исследуемых параметров АБК непосредственно используется при оценке эффективности системы данного уровня иерархии.

Уровень иерархии считается достаточным, если ни один из параметров АБК непосредственно не используется при оценке эффективности системы более высоких уровней.

Таким образом, характерными для исследования АБК является необходимость анализа боевого применения АБК в составе макросистемы, т.е. группировки ВВС.

Обращение к глобальным оценкам эффективности как при формировании рационального множества боевых задач, так и при определении облика обязательно, т.к. роль и место АБК могут быть определены только исходя из анализа его функционирования в системе высшего уровня.

Пример.

1.1 – операция на театре военных действий;

1.2 – типаж группировки (из каких типов), типаж вооружения, численность группировки, состав средств обеспечения боевых действий, эффективность выполнения боевых задач группировки, потери группировки, стоимость группировки, организация боевых действий группировки;

1.3 – перечень боевых задач по каждому типу АБК, требуемый уровень ущерба по каждой боевой задаче, условия выполнения задач, условия базирования, количество аэродромов, характеристики аэродромной сети, время на подготовки групп к вылету;

2.1 – боевой вылет тактической группы;

2.2 – состав тактической группы (боевые наряды), определение боевого наряда (полигонный наряд – без противодействия ПВО; боевой наряд – потери от ПВО – их показатели эффективности), боевая эффективность тактической группы, боевой порядок (интервалы, дистанции), маршруты полета;

2.3 – перечень боевых задач, требуемый уровень ущерба по каждой боевой задаче, условия выполнения, состав вооружения, тактический радиус, времена подготовки, потребная эффективность;

3.1 – см. 2.1 , дальность действия для радиолокационных средств: , где Н –высота (м),D – в свободном пространстве (без помех), подготовка к полету и боевой полет группы;

3.2 – оптимальный состав группы для поражения цели, боевой наряд, боевая эффективность, стоимость применения, способ применения;

3.3 – перечень боевых задач, требуемый уровень ущерба, условия выполнения задач, состав вооружения, время подготовки;

4.1 – подготовка к полету, боевой полет в составе АБК группы;

4.2 – оптимальное распределение ресурсов между подсистемами АБК, функциональные характеристики АБК, боевая эффективность АБК, боевая зарядка АБК, способ боевого применения;

4.3 – задачи решаемые КАВ, требуемая эффективность их решения, условия выполнения, время подготовки;

5.1 – процесс выхода на цель и атака цели АБК

5.2 – оптимальный состав КАВ и его тактико-технических характеристик, способы атаки цели, эффективность выполнения этапов;

5.3 – задачи подсистем КАВ, условия работы, ограничения по габаритам и весу;

6.1 – процесс боевого применения АСП;

6.2 – тактико-технические характеристики АСП, эффективность;

6.3 – массогабаритные ограничения, условия функционирования.

При исследовании эффективности АБК можно выделить 3 основных задачи:

1) задача эффективностного анализа, которая состоит в определении показателей эффективности по заданной структуре и параметрам АБК и условиям применения.

В качестве оптимизируемых параметров выступают стратегии функционирования в рамках системы верхнего уровня в взаимосвязи с другими объектами, образующие макросистему.

2) Задача эффективностного синтеза состоящая в определении оптимизируемой структуры и параметров АБК по заданным показателям, ограничениям и условиям применения.

В основу синтеза положе эффективностно-стоимостной (затратный) принцип выбора.

В качестве компонента стоимостных показателей используется полная стоимость жизненного цикла АБК от разработки до утилизации.

Поскольку синтез АБК состоит в выборе структуры и параметров, то различают задачи структурного и параметрического синтеза.

3) Задача определения рационального типажа, состоящая в определении рационального состава и численности смешанного, т.е. включающего несколько типов АБК, парка, выполняющего заданный во времени объем боевых задач, при заданных ресурсных ограничений на создание и эксплуатацию парка.

Параметрическое описание облика СТС.

Облик СТС представляется структурой и существенные параметры, которые количественно определяют конструкцию СТС, ее функциональные характеристики, полезный эффект и затраты на все этапы жизненного цикла.

Жизненный цикл – это упорядоченная во времени совокупность взаимосвязанных процессов от разработки до утилизации.

Структура СТС определяет состав и тип входящих в нее подсистем, общую компоновку (т.е. их размещение), распределение между ними системных функций (т.е. функциональное назначение).

К существенным относятся параметры, оказывающие влияние на полезные свойства и затраты.

Допустимая область существенных параметров Р выделяется ограничениями, связанными с физической реализуемостью СТС, отпущенными ассигнованиями (финансированием), системой требований нормативного характера и условиями взаимодействия с другими СТС, т.е.

Где - заданные функции ограничений;

- константы ограничений.

Проектируемая СТС представляет динамическую управляемую систему во времени и пространстве.

Следовательно, при формировании ее облика должна быть определена номенклатура основных управлений:

Область допустимых значений .

В конструкции СТС можно выделить особый класс параметров:

значения которых определяются уровнем развития науки и техники в стране и мире (пример: 1) материалы с определенной теплостойкостью или прочностью; 2) ограничения по памяти, быстродействию процессора; 3) химические характеристики топлива) – определяют предельные возможности («в мире» - если кооперация).

Это характеристики материалов, топлива, элементной базы, освоенных технологий и т.д.

В задачу формирования облика они вводятся как константы, но при определенных условиях, если процесс проектирования занимает достаточно большой промежуток времени, они могут изменяться.

Таким образом, для описания облика СТС вводятся ее структурно-параметрическое описание, которое включает:

1) описание структурной схемы;

2) номенклатуру существующих проектных параметров и область их допустимых значений;

3) номенклатуру основных управлений и область их допустимых значений;

4) номенклатуру и значения параметров совершенства технической базы (h).

Структурно-параметрическое описание должно иметь несколько вариантов степени подробности (разные стадии проектирования), должно позволять формировать множества альтернатив.

Достаточно общее формальное параметрическое описание СТС может быть дано многомерным набором Р, который представляется в виде четырех подмножеств (поднаборов):

- многомерный вектор, где

k – элементы, принадлежащие пространству конструкторских параметров: ;

х – элементы, принадлежащие пространству функциональных характеристик: ;

з – элементы, принадлежащие пространству характеристик затрат: ;

w – элементы, принадлежащие пространству характеристик эффективности: .

В качестве примера рассмотрим таблицу примерного состава обликовых характеристик АБК, которые входят в заданные поднаборы.

Табл.1 Примерный перечень параметров авиационного комплекса

параметры и характеристики	системы авиационного комплекса
	планер	силовая установка	оборудование	система наземного обеспечения
конструктивные	состав, весовая сводка, геометрия (размеры и компоновка в пространстве), конструктивная схема, используемые материалы
функциональные	аэродин-ие, уст-ти, упр-ти, прочностные, хар-ки заметности (р/л, ик)	газодинам-ие, дроссельные, высотно-скоростные, заметности (ИК, акустич.)	усл-ия применения, зоны действия, точность, помехоустойчивость, эргономичность, эл-магн-ая совместимость	пропускная способность
	летно-технические хар-ки ( max и min скорости, высоты полета; дальности полета; маневренные; разгона; взлетно-посадочные хар-ки), эффективностная поверхность рассеивания, индикатриссы		степень автоматизации
	надежность, контроле- и ремонто- пригодность, энергопотребление, степень унификации, возможности перебазирования и подвоза материалов
затрат	расход материальных, денежных, трудовых и временных ресурсов на НИР, ОКР, серийное производство, эксплуатация, консервация, утилизация
эффективности	вероятности выполнения задачи или этапа с заданной эффективностью

Анализ табл. 1 показывает, что принадлежащими пространству конструктивных параметров считаются те параметры АК, которые могут быть измерены для уже созданного, но не находящегося в состоянии функционирования АК или его подсистем.

В том случае, если создание АК не завершено, конструктивные параметры с той/иной степенью приближения могут быть получены расчетным путем. Принадлежащим пространству ПФХ считаются те характеристики АК, которые могут быть измерены в состоянии его функционирования.

Большинство характеристик могут быть измерены в процессе летно-технических испытаний. Для не созданного АК функциональные характеристики определяются расчетным путем.

Принадлежащие ПХЗ считаются характеристики денежных, материальных, трудовых и временных ресурсов, расходуемых на всех этапах жизненного цикла АК. Для проектируемого АК они определяются расчетным путем.

Принадлежащие ПХЭ считаются характеристики, определяющие степень приспособленности АК для решения поставленных перед ним задач. Эти характеристики определяются методами моделирования.

В каждом из подпространств параметры и характеристики задаются в виде:

Допустимое множество - это области допустимых (или реализуемых) значений параметров и характеристик, выделенные ограничениями.

Постановка задачи эффективности формирования облика предполагает, что существуют методы вычисления векторов для СТС, определяемой вектором конструктивных параметров, т.е.

- это параметры внешних по отношению к СТС условий, неконтролируемых непосредственно разработчиком СТС, т.е. предполагается, что в каждом пространстве присутствует своя среда, со своей спецификой воздействия на СТС.

При параметрическом задании СТС целесообразно иметь несколько уровней ее параметрического описания, соответствующих фиксированному уровню структуризации СТС.

Различным уровням параметрического описания соответствуют, как правило, векторы проектных параметров разной размерности.

Конструктивные параметры:

В состав конструктивных параметров входят:

1) геометрические;

2) весовые (или массовые) параметры;

Геометрические – определяют форму СТС, ее геометрические размеры, взаимное расположение ее подсистем (т.е. компоновку), а также при заданных материалах – весовые или массовые характеристики СТС.

Весовые (или массовые) характеристики связываются уровнем баланса масс между массой всей СТС и массами отдельных подсистем.

Где - конструктивные параметры j-ой подсистемы.

Область определяется условием:

Где ,

- параметры состояния физической среды.

Функциональные характеристики СТС:

Характеристики, которыми является числовые величины или функции достаточно полно представляющие функционирование СТС в задаче формирования ее облика, называют функциональными.

Функциональные характеристики в отличие от конструктивных параметров К определяются не только материальной основой СТС, но и физическими параметрами среды функционирования ; и для определения каждой характеристики , необходима модель функционирования СТС.

В общем виде каждую функциональную характеристику объекта можно представить в следующем виде:

, где

Z – вектор фазовых координат.

- определяет семейство (комплекс) моделей функционирования.

В общем случае функциональные характеристики или часть из них зависят от управлений и формируя по-разному вектор управления из допустимой области можно получить разные величины х (например: дальность полета, тактический радиус).

При этом каждая конкретная СТС, определяемая вектором , может реализовывать множество значений характеристик в пределах области , т.е.

На практике в качестве характеристик обычно рассматривается значения , определенные при оптимальном или субоптимальном (при определенных допущениях; например: в методе) управлении СТС.

Соотношения при зафиксированных отображает вектор , задающий облик СТС из области в точку , что значительно упрощает описание СТС.

Характерные точки областей функционирования объекта представлены координатами , включаются не только в техническое описание СТС, но и используются в качестве частных критериев в промежуточной процедуре локально оптимизации СТС.

Для уменьшения размерности вектора Х, широко применяется метод агрегирования параметров, при котором СТС, представленная вектором параметров большей размерности, характеризуется агрегированным вектором меньшей размерности с помощью функции агрегирования:

,

Где - функция агрегирования.

Последовательное агрегирования параметров, введение цепочки функций агрегирования:

позволяет исследовать влияние полноты представления СТС на конечный результат решения задачи проектирования.

Эффективностные характеристики СТС.

Эффект непосредственно связан с целью создания СТС. Для многоцелевых СТС критериальная функция, определяющая эффект от создания СТС, является векторной многопараметрической.

,

где - параметры эффекта СТС.

Применяются на ракетах типа «Воздух-воздух», «Воздух-поверхность», «Воздух-космос».

Для получения параметров эффекта разрабатываются системы моделей операций.

Состав системы моделей операций в каждой конкретной задаче проектирования разный, но должен быть минимально достаточным для оценки и обоснования всех существенных параметров СТС, включенных в задачу. В общем случае:

W=F ( , K, h, u(t), Ω, ).

- Структурная схема СТС.

h, K - Параметры конструкции, технического уровня.

Ω - Операция.

Условия, определяемые сотрудничающей системой (аэродромная ВВП, длиной определяет возможности посадки нашей СТС.)

- Условия, определяемые противником.(Характеристики цели.)

- Условия, определяемые физической средой (рельеф, температура.)

Для конкретной СТС К* непосредственно в задачу проектирования чаще всего вводят только эффект, получаемый при оптимальном или субоптимальном (квазиоптимальном) управлении СТС. Поэтому обеспечение управления СТС в моделируемых операциях входят составной частью в задачу формирования облика СТС.(СТС берут оптимальной, противника оптимальным; тактики применения существенно воздействуют на проектирование.)

Если правило выбора оптимального или квазиоптимального управления в исследуемой операции, где – номер операции u(t) U(k), состоящее для всех K, h, то сформировано соответствие при заданных u(t), , Ω, значению .

Для каждых K и h в соответствие ставятся . Этим обеспечивается отображение каждой точки k K в точку (пространство эффекта).

Следует заметить, что в моделях операций параметры K входят чаще всего не непосредственно, а через характеристики x, функционально связанные с K.

Параметры затрат.

При определении затрат на операцию следует различать начальные затраты и затраты на безвозмездные потери (будет ли нанесен противнику ущерб или нет).

При детальном исследовании в рассмотрение вводится ряд компонентов затрат ( )= C . Полный учет затрат ведется не только в денежном выражении, но и в натуральном.

Для вычисления параметров затрат разработаны модели, позволяющие установить связь параметров затрат с конструкционными параметрами конструкционной СТС.

, .

Таким образом, СТС, обладающая параметрами затрат )= C , задается как точка в r–мерном пространстве подмножества характеристик затрат.

Область значений C в этом пространстве ограничена не только допустимыми R K, но и прямыми ограничениями вида: Ф(с)≤0.

При разработке моделей затрат должны соблюдаться следующие принципы:

• Принцип согласованности по исходной информации входов моделей затрат с входами моделей анализа эффективности альтернативных вариантов.

• Принцип полных затрат. В процессе сравнения альтернатив должны учитываться затраты на все этапы их жизненного цикла: проектирование, изготовление образцов, испытания, серийный выпуск…

• Распределение затрат по времени должно быть оптимальным.

Основные задачи параметрического синтеза.

1. Постановка задачи параметрического синтеза для заданной структуры СТС.

2. Проведение декомпозиций с целью установления иерархий показателей эффективности и затрат и существенных связей между подсистемами.

3. Определение вектора существенных параметров для всех уровней иерархии задачи.

4. Построение системы ограничений для всех иерархических уровней.

5. Разработка системы математических моделей функционирования СТС и ее подсистем в операциях и фрагментирующих операций на каждом иерархическом уровне.

Разработка моделей необходима для установления связей показателей эффективности и затрат с вектором существенных параметров СТС для заданного уровня иерархии.

6. Определение неулучшаемых альтернативных вариантов СТС по частным показателям в результате решения локальных задач оптимизации.

7. Решение координирующей задачи – задачи глобальной оптимизации.(Распределение ресурса.)

8. Послеоптимизационный анализ.

Структурное описание облика СТС.

Структурой системы будем называть ее организацию из отдельных подсистем и элементов и их объединение с их взаимосвязями, которое определяется распределением функций выполняемых системой и целями её функционирования. Таким образом, структура – способ организации целого из составных частей. Типичными характеристиками структуры СТС являются:

• Число уровней иерархии в системе (одно- и многоуровневые);

• Количество подсистем и элементов;

• Степень централизации в СТС, то есть принцип управления и подчинения.

По степени централизации можно выделить децентрализованные, централизованные, смешанные системы.

Децентрализованная система – решение отдельными элементами системы принимаются независимо и не корректируются системами более высокого уровня.

Централизованная система – задания отдельным элементам системы выдаются одним элементом более высокого уровня.

Смешанная система – управление некоторыми функциями (или этапами их выполнения) происходит централизованно, а другими децентрализовано.

Рассмотрим типовой вариант представления структуры СТС. На верхнем уровне иерархии рассматривается система в целом.

1 уровень – СТС как совокупность подсистем, выделенных по функциональному принципу.

2 уровень – каждая подсистема – совокупность агрегатов.

3 уровень – агрегат – совокупность узлов.

4 уровень – узел – совокупность деталей.

Между смежными уровнями иерархии существуют как однонаправленные, так и двунаправленные связи. Однонаправленные связи возникают из-за требований подсистемы более высокого уровня к подсистеме нижестоящего уровня. Двусторонние связи между смежными системными уровнями возникают в случае взаимовлияния вышестоящей подсистемы на нижестоящую и наоборот.

Между подсистемами одного системного уровня также могут существовать двунаправленные связи, если существует элемент, общий для двух подсистем.

Подсистемы первого и нижележащих системных уровней образуют изолированные группы, замыкающиеся только на один элемент вышележащего уровня.

Делаются допущения об отсутствии связей между элементами систем несмежных уровней.

Основные понятия теории графов.

Универсальным аппаратом для описания структуры СТС является язык графов.

G -совокупность двух конечных множеств:

Множество точек – вершины;

Множество пар вершин – ребра.

G =(x, u)

Представим наглядно множество точек плоскости, называемых вершинами, и множество отрезков, соединяющих все или некоторые из вершин, называемых ребрами.

Если на каждом ребре задается направление, то граф называется ориентированным, а ребра – дугами (направленный отрезок, соединяющий две вершины). Ребра, имеющие одинаковые конечные вершины – параллельные. Ребро, конечные вершины которого совпадают, называется петля. ( - параллельные, петля.)

Пусть G – такая последовательность ребер, в которой конец каждого предыдущего ребра – это начало следующего. Путь, в котором никакое ребро не встречается дважды – простой. Путь, где вершины не встречаются дважды – элементарный. Цикл – путь, начальные и конечные вершины которого совпадают ( ).

Длина пути (цикла) – число ребер (пути или цикла).

Графы удобно представлять в виде матриц, которые называются матрицы смежности или инцидентности.

Вершины х и у являются смежными, если они различны и если существенная дуга, идущая из х и у. Дугу называют инцидентной в вершине, если она заходит в эту вершину или исходит из нее. Два ребра инцидентные одной и той же вершине – смежные. Обозначим через ,…, вершины графа, а через ,…, его дуги. Введем числа :

Квадратичная матрица – матрица смежности графа размерности .

Если между узлами имеются кратные связи, то значения элемента равняются числу связей.

Введем числа:

– матрица инцидентности для дуг графов.

Матрица смежности
i	11	22	33	44	55
11	00	11	00	11	11
02	00	00	00	00	00
.3	00	00	00	00	11
44	00	11	11	00	11
55	00	00	10	11	00

Матрица инцидентности
i	11	22	33	44	55	66	77	88
11	11	11	11	00	00	00	00	00
22	--1	00	00	--1	00	00	00	00
33	00	00	00	00	--1	00	00	11
44	00	--1	00	11	11	11	--1	00
55	00	00	--1	00	00	--1	11	--1

Граф G – полный, если любые две его различные вершины соединены ребром и он не содержит параллельных ребер.

G - без учета ориентаций дуг – неориентированный.

Для неориентированного графа понятия: дуга, путь, контур заменяются на: ребро, цепь, цикл соответственно.

Ребро – отрезок, соединяющий две вершины.

Цепь – последовательность ребер.

Цикл – цепь, у которой начальные и конечные вершины совпадают. Он называется простым, если не проходит ни через одну вершину более одного раза.

Определения, служащие для характеристики неориентированных графов:

Степень вершины – число ребер, инцидентных ей.

Вершина степени один – висячая.

Вершина степени ноль – изолированная.

Граф G – связный, если для любых двух его вершин существует путь, их соединяющий.

Связный граф без циклов – дерево.

Если дано множество вершин a, b, c, то дерево можно построить так:

a - Возьмем начальной – корень дерева. Т.о. дерево можно построить, последовательно добавляя ребра в его вершинах. Дерево с n вершинами имеет n-1 ребро.

Операции над графами

Объединение графов - : множество вершин - объединение множеств вершин графов . Множество ребер – объединение множества ребер .

Пересечение – граф множество его вершин – пересечение вершин , множество ребер – множество пересечения ребер .

Кольцевая сумма: – граф, порожденный на множестве ребер, присутствующих либо в , либо в , но не принадлежащих их пересечению.

С топологической точки зрения можно ввести следующую классификацию структур системы СТС:

1. Несвязные структуры.

2. Двудольные структуры.

3. Кольцевые структуры.

4. Максимально связанные структуры.

5. Последовательная структура.

6. Радиальная структура.

7. Древовидная структура.

Т.о. граф аналитически представляется в виде матрицы смежности или инцидентности. Элемент матрицы смежности принимает 0 или 1 в зависимости от того, имеется ли в графе дуга между -ым и -ым узлом. Если между вершинами имеются кратные связи, то значение равняется значению этих связей.

Элемент матрицы инцидентности равняется 1, если -ая вершина – начальная для ребра , равняется -1, если - конечная для -го ребра, равняется 0, если -ая вершина не связана с -ым ребром.

Дуги структурного графа описывают отношения между элементами проектируемой системы. Физический смысл их таков: они определяют пространственные размеры, стоимостные характеристики, массогабаритные, временные.

Матрицы смежности и инцидентности, отображающие структуру проектируемой системы, могут рассматриваться как обычные числовые, над которыми определен ряд операций. Это позволяет использовать матрицы для непосредственного определения характеристик систем.

Рассмотрим техническую систему, структура которой состоит из трех системных уровней: 0,1,2. Связи в системе односторонние. На первом системном уровне две подсистемы. На втором первой подсистеме соответствует три агрегата, второй – два. Матрица смежности для нашего случая:

	1	2	3	4	5	6	7	8
1	0	1	1	0	0	0	0	0
2	0	0	0	1	1	1	0	0
3	0	0	0	0	0	0	1	1
4	0	0	0	0	0	0	0	0
5	0	0	0	0	0	0	0	0
6	0	0	0	0	0	0	0	0
7	0	0	0	0	0	0	0	0
8	0	0	0	0	0	0	0	0

Кратные связи в системе возникают, если между элементами системы имеется несколько типов отношений. Если структура системы достаточно сложна, то граф её ограничений может быть не плоским, а простым. Тогда элемент матрицы смежности может иметь третий индекс, соответствующий слою пространственного графа.

Применение сигнальных графов для представления структуры в линейных моделях.

Вершина графа соответствует компоненту системы, дуги – каналы передачи воздействий от первого компонента к другому. Каждой вершине ставится в соответствие переменная, имеющая номер, совпадающий с номером вершины. Начальная вершина – нулевая. Каждая дуга имеет весовой коэффициент или коэффициент усиления, с которым передается воздействие между смежными вершинами. Если воздействие при передаче усиливается, то коэффициент усиления положительный, ослабляется – отрицательный. Индекс коэффициента усиления двузначный: 1 – номер воздействующей вершины, 2 – вершина, на которую воздействуют. Значение переменной, определяющей вершину, находится как результат прохождения воздействия через все вершины, является материнским по отношению к данной. Воздействие вычисляется как перемножение аргумента на коэффициент связи. Граф, обладающий этими свойствами – сигнальный. Пример сигнального графа:

Система уравнений:

Чаще метод представления структуры в виде сигнального графа используется для отображения системы управления. Удобство заключается в возможности формального преобразования структуры системы с целью её упрощения.

Соединение и его преобразование	Формула определения результирующего сигнала	Название соединения
	,	Последовательное
		Параллельное
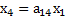	,	Замкнутый контур (обратная связь)

Отображение структуры системы в нелинейных моделях.

Основные типы структурных взаимодействий компонентов системы:

• Последовательное

• Параллельное

• С обратной связью

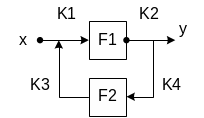
Для типовых структур мы провели преобразования. Х –входной вектор, - передаточные функции, - коэффициенты связи.

Для СТС предложены различные методы структурного описания. Наиболее широко применяемые среди которых:

1. Задание структуры с помощью матрицы признаков (морфологический);

2. Задание структуры с помощью и/или графа.

Задание структуры матрицей признаков.

Пусть для описания структуры достаточно указать n её составляющих - признаков. Пусть i-ый признак имеет альтернатив (возможных реализаций). Тогда полный список, включающий полный перечень альтернатив, определяет множество структур, которое будет определятся числом N= Один из вариантов предлагаемой матрицы признаков: если в каждой строке i зафиксировать один из элементов j, то набор из них – возможный вариант решения. Всего таких вариантов N. Очевидно, что среди N решений найдутся работоспособные и неработоспособные. Поэтому при генерации вариантов должна решаться задача их функциональной совместимости.

Пример.

Ракета «Воздух-Воздух». 12 признаков. - альтернативные

	- Большая	-Средняя	- Малая		Дальность действия
	- одна	- две			Количество ступеней
	- нормальная схема	- «утка»	- схема с поворотным крылом		Тип аэродинамической схемы
	– аэродинами-ческая	- газодинами-ческая (поворот-ное сопло)	- газодина-мическая(интерцептор)	- комбини-рованная	Тип системы создания управ.сил и моментов
	- самонаводя-щаяся	- самонав. С инерцион.кор.участком			Тип системы наведения
	- активное	- полуактивное	- пассивное	- комбиниро-ванное	Тип ГСН

Представление структуры в виде и/или графа.

И/ИЛИ граф – граф, в котором множество вершин разбито на два класса:

И-вершины – конъюктивные,

Или-вершины – дезъюнктивные.

Каждая И вершина содержательно интерпретируется как подсистема объекта проектирования определенного уровня иерархии, а ИЛИ вершина соответствует альтернативным вариантам структур подсистемы. И/ИЛИ графы наиболее хорошо приспособлены для задач, которые естественным образом разбиваются на взаимонезависимые.

Каждая «И-вершина» содержательно интерпретируется как подсистема объекта проектирования, определенного уравнения иерархии. «ИЛИ-вершина» соответствует альтернативным вариантам структурных подсистем.

Представление И/ИЛИ графов наиболее хорошо приспособлено для задач, которые естественным образом разбивают на взаимно независимые.

Рис.1

Вершины, из которых выходят только «И-дуги»-«И-вершина».

Вершина, из которой выходят «ИЛИ-дуги»-«ИЛИ-вершина».

Представление структуры И/ИЛИ графа называется морфологическим деревом.

При генерации структуры с помощью И/ИЛИ графа также должна контролироваться совместимость признаков технических решений.

Пример: (Задача поиска маршрута).

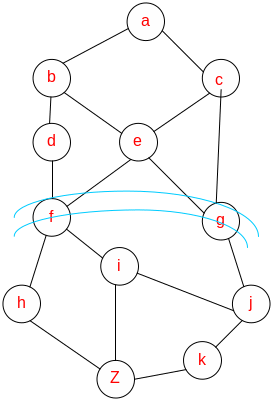
Рис. 2

Решение:

Рис.3

Решение представляет решающее дерево T ,которое определяется следующим образом:

Исходная задача-корень дерева;

Если исходная задача является «ИЛИ» вершина, то в дереве T содержится только один из ее приемников вместе со своим решающим деревом.

Если исходная задача «И» вершина, то все ее приемники вместе со своими решающими деревьями содержатся в T.

Следовательно, «И/ИЛИ» графы способны описывать все возможно допустимые структуры проекта и его подсистем.

Множество таких описаний, упорядоченных выделением уровней структурного описания отвечает в глубине проработке структуры на различных этапах проектирования

Пример: (ракета «воздух-воздух»).

1)Управление режимом работы двигателя.

2)Управление программой расхода топлива.

3)Управление формой траектории.

4)Управление параметрами аэродинамической схемы за счет изменения положения крыла или размера площадей управляющей поверхности.

5)Управление параметрами для поражения боевой части за счет использования

Преобразование структуры проектируемых систем

Преобразование структуры сводится к двум процессам:

-декомпозиция;

-агрегация;

Декомпозиция-это преобразование проектируемой системы, когда какой-либо из компонентов системы заменяется новой группой компонентов таким образом, что отношение, вводимое для данной группы, совпадает с соотношениями связывающими декомпозируемый компонент с остальными компонентами системы внешней средой.При этом отношение между компонентами внутри группы дополняет множество проектируемых систем.

В применении к задачам оптимизации декомпозиция состоит в разбиении основной задачи оптимальности на несколько связанных друг с другом экстремальных задач значительно меньшей размерности; эти подзадачи образуют первый уровень в иерархии системы.

На первом уровне решаются подзадачи при произвольных связях, определение этих связей составляет задачу второго уровня.

Агрегирование- такое преобразование структуры системы ,при котором группа компонентов системы заменяется новым компонентом таким образом, что отношения связывающие вводимый компонент с другими компонентами системы и внешней средой совпадает с отношениями агрегируемой группы. В этом случае отношение между компонентами внутри группы исключаются из множества отношений системы. Следовательно, агрегация-это процесс построения системы, обладающей заданными свойствами , путем объединения отдельных подсистем с известными характеристиками

Если декомпозиция систем вызвана необходимостью получения объема информации достаточной для реализации процесса проектирования, то агрегирование необходимо для управления процессом проектирования и оценкой эффективности и принимаемых проектных решений.

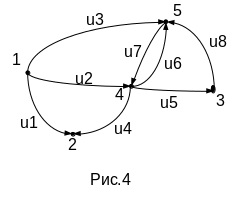
Пример: (преобразование структуры проектируемых систем для двух вариантов.)

А) Декомпозиция

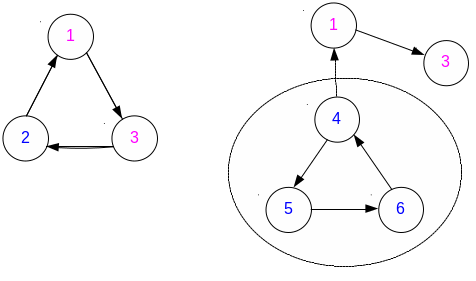
Рис.4

Б) Агрегирование

Рис.5

Преобразование структуры вызывает изменение структуры графа, то есть его матрицы смежности и инцидентности

При декомпозиции:

Размерность соответствующих матриц увеличивается, элемент матрицы смежности принимает значение «0» или «1» в зависимости от того имеется ли в графе дуга между i-ым j-ым углами. Если между углами есть кратные связи , то значение соответствующего элемента матрицы равно числу этих связей.

Пусть в системе есть n-компонент и матрица смежности имеет размерность [n×n].Декомпозиция к-ый компонент которой заменяется подсистемой, состоящей из вершин нового компонента.

В этом случае матрица смежности увеличивает свою размерность до следующей.

(n+m-1)×(n+m-1)

Рассмотрим метод декомпозиции, основанный на распределении ресурсов.

Пусть имеется модель синтеза систем

extr x Si, i=

Функции цели fi, характеристики gi и множество значений параметров системы в пространстве состояний Si связаны с i-ой подсистемой проектируемой системой.

Векторы xi имеют n-компонентов, а gi m-компонентов.

Задача 1 допускает интерпретацию, как задача оптимального распространения ресурса по подсистемам.

Пусть количество ресурса выделено i-ой подсистеме и равно yi, тогда возникает условие.

Предполагая, что ресурс между подсистемами распространяется оптимальным образом, получим следующие подзадачи синтеза для каждой i-ой подсистемы:

extr fi(xi)

qi(xi) yi,

x Si

Тип экстремумов в задаче 1 и 3 совпадают. Экстремальное значение fi(xi) является функцией выделенного данной подсистемой ресурса

Обозначим этот ресурс yi

extr fi(xi)→ yi

extr (yi)

В случайной декомпозиции преобразований структура будет иметь вид

В результате оптимальных ресурсов от каждой системы получаем наилучшую систему

Рис.6

Рассмотрим подход разбиения оптимизационных систем на подсистемы.

Проблема:

Исходное множество компонентов большое, его необходимо агрегировать. Пусть в состав проектной системы S входит m-компонентов, то есть g-множество подсистем.

S={c1,c2,…cm}

Вводится система разбиения множества S

E={ }, ={ }

S= ; = ; p,q= ; p q

Пусть каждый компонент системы Ck n-мерный векторный показатель Ck(xi), xi= .

q(x,y)=q(y,x)-определяют степень близости между компонентами. Компоненты считаются тем более положительными, чем меньше .

Зафиксируем число элементов разбиения.

Для каждого подмножества элементов системы определим базовый компонент вокруг которого будем формировать агрегат следующим образом.

Таким образом каждому разбиению соответствует система центров.

…

Хорошие разбиения, которые удовлетворяют условию:

q (xi, ui) ≤ q(xi,ur) I Iτ, где r,j

ur-мера близости, которая определяет возможность включения компонента в агрегат.

Примем за меру качества разбиения:

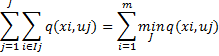
Условие позволяет свести построение оптимального разбиения к задаче отысканиятакого набора векторов j= , на котором правая часть достигает минимума:

Определения структуры в виде (5)-(9) повторяет задачу кластерного анализа

№	Название	Функция близости
1	Эвклидово расстояние	q(xi,yi)=
2	L1-норма	q(xi,yi)=
3	Супремум-норма	q(xi,yi)= }
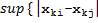4	Ln-норма	q(xi,yi)=

Алгоритм оптимальной структуры состоит из последовательного решения следующих задач:

1. Формирование допустимого множества обобщенных подсистем.

2. Формирование морфологической матрицы (матрица-признак).

3. Интервальное задание (коэффициент эффективности aij), входящее в состав морфологической матрицы.

4. Формирование морфологической матрицы несовместимости Q={ 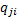} (признаки в морфологической матрице могут быть несовместимы)

5. Генерация варианта структуры с помощью ДСЧ и проверка принадлежности набранных структур матрицы Q.

6. Проверка условия функциональной реализуемости варианта сгенерированной структуры.

7. Проверка условия физической реализуемости.

8. Выделение множества альтернативных структур, соответствующих результатам оптимальности.

Целями структурного анализа является следующее:

1. Разработка правил символического отображения систем.

2. Оценка качества структуры системы

3. Изучение структурных свойств системы в целом и ее подсистем.

4. Выработка заключения об оптимальности структуры и рекомендации по ее совершенствованию.

Формирование задач, поставленных перед СТС.

Формирование облика СТС проводится при моделировании ее функционирования в типовых операциях, для выполнения которых предназначена проектируемая СТС.

Выявление и классификация производится в следующем порядке:

1)Составляется полный перечень задач по всем видам применяемых СТС на всех иерархических уровнях.

2)Все множество задач сводится к ограниченному числу обобщенных типовых задач. Число типовых задач должно быть минимальное, но достаточное для оценки и отбора лучших. По каждой типовой задаче составляется сценарий, т.е. ее словесное описание.

3)Описание по каждой задаче формализуется ,для чего составляется схема последовательности действий СТС во времени и пространстве, от начала до завершения задачи.

4)Основной формой конкретизации задачи являются операции, следовательно, задачи стоящие перед СТС задаются набором типовых операций ,причем каждая операция ставится как многоцелевая, а в каждой операции может быть и многокритериальность.

Типично следующее представление задач, поставленное перед объектом, достаточное для начального этапа проектирования:

1.Набор типовых операций СТС или объекта, определенных в значительной степени словесно с минимальным числом количественных параметров.

2. Ориентировочные значения наборов параметров внешних условий .

3. Рекомендованная номенклатура параметров эффекта СТС в каждой из операций

4. Желаемое значение некоторых из показателей эффекта, абсолютная или по отношению к СТС предшествующему поколению, к которому следует стремиться.

s-некоторые из компонент векторов в рамке критериев.

s

wos –заданные числа.

5. Ограничения на нижний допустимый уровень некоторых из характеристик xj , j= и параметров эффекта wi, т.е.

i

6. Если цель и ограничения представлены таким образом, то задачи, стоящие перед СТС, можно определить, как задачи проектирования.

={ , , }

-желаемое значение вектора эффекта

-нижняя граница эффекта

-желаемые характеристики нижнего значения

Отдельно должен быть указан желаемый уровень затрат на СТС и должно выполняться условие C (желаемый уровень затрат).

C→

Векторы задачи проектирования и ограничения на затраты -это еще не аналоговое техническое задание, а некоторые числовые рамки для начального этапа разработки, для которого в дальнейшем допустимы отклонения.

При формировании облика СТС все множество типизированных задач, а, следовательно, и операционных моделей удобно разбить на группы , принадлежащие следующим иерархическим уровням:

1.Элементарная операция.

2.Операции однократного применения СТС законченным циклом действий, включающих последовательность элементарных операций.

3.Многократный повтор циклического применения СТС в ходе операций.

Для формирования облика создается система операционных моделей, которая разворачивается по двум иерархическим структурам.

4.По этапам жизненного цикла, т. е моделям затрат.

Иерархическая система

Рис.7

Операции иерархии

Рис.8

Модель затрат

Рис.9

Общая схема и типовые задачи параметрического синтеза.

Возможные постановки:

Постановка1 (На реальных этапах )

w→max (максимизация параметров эффекта.)

C< , T

Постановка2 (На этапах проектирования)

c→min (минимизация затратов)

w , T

w,c- показатели эффекта, затрат.

, - ограничения.

T – момент начала эксплуатации.

- ограничения на момент начала эксплуатации.

При одинаковых внешних условиях обе постановки эквивалентны и приводят к одинаковому результату

Обозначим варьирующие параметры на входе задач проектирования через z=(z1…zp), общий эффект СТС через А, общие ограничения, налагаемые на решение задач-G.

Будем предполагать, что для решения задач

A→max

G b

Необходимо представить

A=F(z), G=g(z) , где

F(z)-целевая функция;

g(z)-функция ограничений;

Следовательно, задачу проектирования можно представить, как задачу математического программирования.

z0= argmax F(z)

z={z/g(z b}

Процедуру решения данной задачи можно представить следующей блок-схемой.

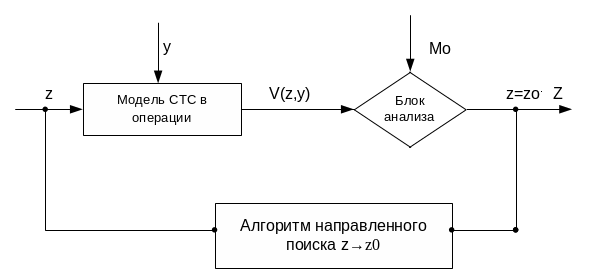
Рис.10

Предполагается, что к этому моменту времени структура СТС и стоящие перед ней задачи виде моделей операции уже сформированы.

Поиск оптимального решения z0 по приведенной схеме производится в итерационных циклах.

z – вектор парируемых параметров;

Z – область допустимых значений z;

y – вектор внешних условий (независимых параметров);

V – вектор числовых показателей полезных свойств СТПС при заданной паре z, y;

– вектор задачи проектирования для заданной операции;

={ , , }

- решение задачи, при которой выход V0 max0 близок к желаемому M0.

-полная система математических моделей операций, устанавливающих связь между входными параметрами z y и выходными функциями V(z,y) для СТС в данной операции применения.

- это операция сопоставления численных значений функций V(z,y) и параметров задачи M0 и принятия решения о прекращении процесса оптимизации или повторной итерации.

В зависимости от состава компонент вектора M0 могут быть разные постановки.

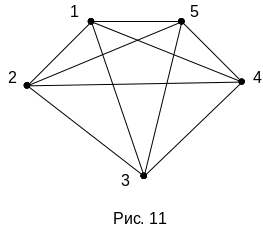
Если оценка и оптимизация СТС производится на уровне его конструктивных характеристик, то с следует принять, что z=k, V=x и параметрический синтез в этом случае по следующей схеме

Рис.11

В случае оценки СТС по параметрам эффекта в операции принимается, что

Z=k; V=w

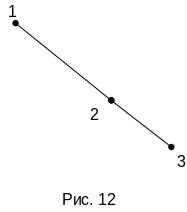
Блок-схема параметрического синтеза выглядит следующим образом

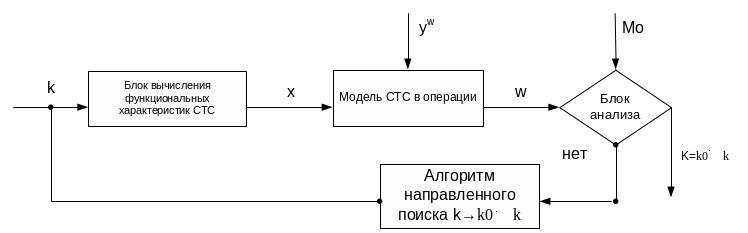
Рис.12

Mo={Wos,Woi,Xoi}

На самых ранних этапах разработки иногда в качестве варьируемых параметров могут использоваться функциональные характеристики, в этом случае

Z=x, V=W

Ограничения на область допустимых значений функции ограничений на x может быть внесено через уровень затрат

Рис.13

Примечание:

На всех схемах затраты зафиксированы и представляют собой дополнительные ограничения при выделении областей k или x .Также во всех схемах определение функциональных характеристик или показателей эффекта проводится при оптимальных управлениях СТС в операциях.

Учет расчета внешних условий

При синтезе СТС необходимо учитывать все многообразие внешних условий и полную картину влияния внешних условий дает так называемая матрица эффективности.

Для этого область изменений z Z и y Y, разбив сеткой опорных точек и в качестве столбцов матриц примем значения

И в качестве строк матрицы значения, а на пересечении строк и столбцов , то есть в узлах сетки задаются целевой функции, полученной на модели операции

Типовые задачи синтеза.

Рассмотрим несколько типовых постановок и методов синтеза при разных постановках задач проектирования .

1. Получение полного образа области допустимых решений (множество всех альтернатив в пространстве выходных показателей эффекта)

Для этого выделяется множество опорных точек, достаточно полно представляющих дополнительно областей Z и для этих точек находятся методом моделирования операций.

Определение V (эффект) дает полное представление о достижимых значениях параметров эффекта для всех проектных решений; выбор лучших альтернатив сводится к операциям сравнения, заданных значениями в векторе .

M0(Vos, Voi, Zoi)

Vs(z)→Vos

Voi(z) Voi

2. Проектирование СТС по тактико-техническому заданию (ТТЗ).

Задача проектирования содержит систему чисел Voj и требуется найти хотя бы одно решение ZoЄ Z, удовлетворяющие условию Vj≥Voj (1).

Решение является любая точка Zo, для которого выполняется данное условие (1).

Если условие (1) не выполняется, то необходимо корректировать ТТЗ и формировать новое значение Voj. Для определения оптимального решения можно использовать любой алгоритм условной оптимизации, для котой выполняется условие g(Zo) ≤ b, а далее выполняется условие (1).

3. Предельное решение задачи проектирования.

При заданной номенклатуре показателей Vj, j= 1,p путем вариации значений параметров z Є Z ищется такое значение VojП, при котором область решения

Zo={Zo| Voj(Zo) ≥ VojП| ->ZoП

стягивается в точку

Метод поиска предельного решения состоит в последовательном переводе каждой из ограничивающих функций Voj в разряд целевой с выполнением процедуры ее максимизации.

Найденное решение ZoП и соответствующие ему значения VojП являются предельными.

Найти точку ZoП, для которой выполняется неравенство, нельзя.

Мы в этом случае минимизируем расстояние между фактической и желаемой функцией.

Zo^П Z^П

Z

Поскольку ЦФ могут быть различной физической размерности, необходимо их форматировать.

4. Оптимизация в случае скалярного критерия

A=F(V)

F(V) – заданная скалярная ЦФ

Vj, j=1,p – ЦФ

A=F(V) = , Jj≥0

Vj пронормированные ЦФ, т.е. безразмерные.

В данном случае требуется найти решение

Zo=argmax F(V)

z є Z

g(Zo) ≤ в

При 4 подходе в решение задачи вносятся определенные произвольные связанные с использованием того или иного вида свертки глобальной ЦФ.

5. Векторная задача оптимизации

Это постановка не решения до конца задачи выбора лучшей альтернативы Zo, позволяет существенно сократить множество возможных решений.

Пусть для проектировщика представляют ценность все целевые показатели Vj, j=1,p и он не утверждается в выборе свертки F(Vj).

В этом случае можно строгими методами выделить в область эффекта V доминирующие другие при любом виде монотонной ЦФ F(V).

Одним из таких приемов, позволяющих сузить область поиска решения в пространстве Z и пространстве эффективности V является определение решений, оптимальных по Парето.

Рассмотрим геометрическое пояснение этого решения для случая, когда вектор показателей двумерный

V=(V1,V2)

Очевидно, что из любой точки области V, включая граничные, но не принадлежащие дуге ab, можно перемещаться, одновременно увеличивая оба показателя.

И только при достижении дуги ab эта возможность будет утрачена, т.е. при перемещении по дуге ab один из показателей будет расти, а другой обязательно уменьшаться.

Объекты допустимой области Z, породившие точки дуги ab, называются эффективными или оптимальными по Парето и доминируют все остальные объекты области Z.

В задаче с многомерными векторами

V(Z)=(V1(Z), V2(Z),…, Vp(Z))

альтернатива

Z⁽¹⁾ доминирует по Парето альтернативу Z⁽²⁾, если Vj(Z⁽¹⁾) ≥Vj(z⁽²⁾), j=1,p j ≠l и хотя бы для одного j такое неравенство является строгим, т.е.

Vj(Z⁽¹⁾) > Vj(Z⁽²⁾) j=l

Решение векторной задачи оптимизации состоит в нахождении всех эффективных точек множеств Парето и Z: П(V,Z)

В большинстве задач оптимального проектирования полезно находить множество эффективных точек П(V,Z) и уже только на нем, а не на всем допустимом множестве Z, строить процедуры окончательного выбора единственного решения (см. лекцию последовательного анализа вариаций)

Задача проектирования состоит в определении оптимального параметров по ЦФ высокого уровня иерархии.

Предварительно все множество Z сужается до множества, оптимального по Парето, по системе критериев, определяющих оптимальные характеристики 1 объекта проектирования.

Например, проектируем авиационную пушку. Ее эффективность определяется калибром, темпом, начальной скоростью. Для определения эффективности параметров надо выйти на уровень воздушного боя.

6. Максимизация одного из показателей Vj, j=1,p и переводе остальных при этом в систему ограничений Ve – к-то один критерий.

Zo=argmax Ve при условии z є Z

Vj(Zo) ≥ Vjo, j=1,p; j ≠ l

Задача выбора типажа

Система нескольких типов СТС, относящихся к одному виду, называется типажом.

Очевидно, что наиболее эффективно сможет выполнить каждый конкретный тип задач лишь та СТС, которая специально синтезирована для решения этого типа задач.

Также понятно, что число типов СТС образующих эксплуатационный парк, должно быть не только конечным, но и весьма небольшим.

Объективная основа для постановки задачи выбора рационального типажа обусловлено следующими причинами:

1. Снижение стоимости серийного производства при производстве одной СТС по мере увеличения размера серии.

2. Многократно возрастающая стоимость и сложность подготовки обслуживающего персонала и обеспечение запаса соответствующих материалов и запчастей, необходимых при эксплуатации многотипного парка СТС.

Под задачей типажа СТС понимается задача определения рационального по принятому критерию эффективности качественному и количественному составу парка СТС, выполняющий заданный по времени объем цел задач.

Отметим наличие взаимосвязей задач синтеза и типажа.

Решение задачи типажа невозможно до тех пор пока не заданы облики альтернативных вариантов СТС, т.е. не получено решение задачи синтеза для этих вариантов, а решение задачи синтеза СТС невозможно до тех пор пока не определен круг целевых задач, возможных на СТС данного типа.

Наличие указанной взаимосвязи вынуждает особенно на ранних этапах проектирования рассматривать эти задачи совместно как составляющие одной проблемы «синтез-типаж».

Решение задачи «синтез-типаж» требует не только рационального выбора компонент вектора типа СТС, но и отыскание разбиения всего множества целевых задач S на подмножества Sk, решаемые каждым конкретным типом.

Решение задачи типажа рассматривается в следующих постановках:

Задача А: задан суммарный объем целевых задач S=(S1,S2,…,Sn), который должен быть решен в ходе выполняемых операций, формируемых парком СТС.

Задан набор альтернативных вариантов СТС

X={xj}, j=1,k

Обликовые характеристики этих СТС известны.

Необходимо определить рациональный состав парка СТС, обеспечивающий выполнение заданного объема целевых задач при минимальных затратах на разработку, серийное производство и эксплуатацию в течение полного жизненного цикла СТС.

Задача В. В отличие от задачи А, где все СТС считаются вновь разрабатываемыми, здесь предполагается, что к моменту формирования парка в эксплуатации имеются Y={yj} старых типов, производство некоторых из которых уже прекращено, а некоторых еще продолжается.

В этом случае при вычислении суммарных затрат этих типов учитываются только затраты на их эксплуатацию и серийное производство, если оно продолжается.

Задача С. Она представляет собой динамичный вариант задачи В.

Существо этой задачи сводится к рассмотрению не единовременного акта формирования рационального парка, а непрерывного процесса замены одних типов СТС, морально или физически устаревших, другими, более совершенными, с учетом временной динамики изменений, возлагаемых на парк целевых задач.

Рассмотрим формализацию этих задач.

Постановка задачи А: требуется найти в-р

X={xj}, j=1,k,

доставляющий min функции

Σj(xj)= j (xj)* ij

при следующих ограничениях

Si ≤ ; i=1,n; j=1,k

Xij≥0; i=1,n; j=1,k

Xj = ≤ xj’

n – количество подлежащих выполнению целевых задач;

i – тип целевых задач;

Xij – количество СТС j-го типа, выделенных для решения задач i-го типа с заданным уровнем эффективности;

СΣj (Xj) – суммарные затраты на разработку, производство и эксплуатацию СТС j-го типа;

Xj* - заданное ограничение на количество СТС j-го типа.

Определение Xj сводится к определению потребной численности СТС j-го типа, обеспеченных при решении задачи i-го типа ущерб противнику не менее заданного.

Задача В. Требуется найти вектора X={xj}, j=1,k,

доставляющие минимум функции

Σj(Хj)+ j (Уj)= j (xj)* ij+ j (Уj)*

при ограничениях

Si ≤ ; i=1,n; j=1,k

Xij≥0; Yij≥0, i=1,n; j=1,k

Xj ≤xj’; Yj≤ Yj’

Si-количество подлежащих боевому выполнению боевых задач i-ого типа;

Yij-необходимое количество СТС задач j-ого типа для решения задач i-ого типа с заданным уравнением эффективности.

З адача С.Отличия постановки задачи С по сравнению с постановкой задачи В состоит в следующий плановый период Tп=[t0,t max] разбивается на m в общем случае неравных интервалов t ti и на каждом из интервалов решается задача В, причем результат решения задачи В на (i-1) интервале, т.е. конечный состав парка для ( i-1) интервала, выступает в роли начальных условий для величин Xj и Yj для задачи В на i-ом интервале – «принцип короткосрочного планирования».

Метод существенных связей при параметрическом синтезе СТС.

В соответствии с системным подходом формирование ошибки СТС как элемента большой системы должно проводиться с учетом его взаимосвязей с внешней средой и с другими СТС, входящими в состав большой системы. В свою очередь облик подсистем, входящих в состав синтезируемой СТС, должен формироваться с учетом их взаимосвязей с внешней средой и между собой и в интересах повышения эффективности СТС, в состав которой они входят.

При этом функционирование систем, входящих в СТС, основано на различных физических принципах и их проектирование выполняет разные коллективы разработчиков.

В этой связи возникает необходимость реализации процедуры условно автономной каждой из подсистем с учетом требований и обеспечения системного подхода.

СТС

Подсистема 1

Подсистема 2

Основным подходом при решении задачи синтеза СТС являются декомпозиция СТС, т.е. ее разбиение на ряд подсистем с последующим агрегированием решения, полученных для каждой подсистемы в интересах выработки окончательного решения.

Объединение частного решения в интересах общего выполняет процедура координации. Цель декомпозиции – упростить задачу формирования ошибки СТС путем рассмотрения ее оп частям. А в организационном плане- предоставить автономию разработчикам подсистем, но при этом сохранить основные рычаги управления за разработчиком большой системы за счет координации.

Координация- задача вышестоящей управляющей системы обеспечить согласованное функционирование нижестоящих систем в интересах глобальной цели, поставленной перед всей системой.

Декомпозиция задачи синтеза состоит в разделении общей задачи на ряд задач субоптимизации по частным критериям оптимальности, которые имеет существенно меньшую размерность и допускает раздельное решение, давая в совокупности тот же результат, что и глобальная задача оптимизации.

На практике задачи синтеза не могут быть подвергнуты декомпозиции на полностью независимые задачи, так как возможности такой декомпозиции означает полную автономность и независимость систем.

Процедура декомпозиции включает:

1. Выделение отдельных в максимально возможной мере независимой от общей задачи подзадач, т.е. подзадач, которые будут решаться по отдельностиж

2. Обоснование состава существенных связей подзадач между собой и задач более высокого уровня иерархии;

3. Выделение частных критериев оптимальности для каждой из задач, адекватных глобальному критерию оптимальности.

Под существенными связями подзадач будем понимать те из ее параметров, которые не могут быть выбраны оптимальным образом на основании решения задачи субоптимизации по частным критериям оптимальности в силу их взаимозависимости от параметров других подзадач или задачи верхнего уровня иерархии. В этом случае результат субоптимизации решения подзадачи выражается как функция существенной связи, а при решении координирующей задачи оптимизируются только существенные связи, и тем самым фиксируются оптимальные значения параметров подзадач, выбранных на предыдущем этапе функции существенных связей.

Распространим на систему, содержащую проектируемую СТС, следующие общие положения декомпозиции:

1. Систему можно исследовать по частям, разбив ее на n иерархических уровней; nє 1,q.Один из иерархических уровней должен включать разрабатываемый объект со связями, идущими от него вверх, т.е. к q=n+1, вниз к q=n-1,и по горизонтали к подсистемам того же уровня.

2. Уровень n вырезается из тела системы. При этом в местах сечений возникают силы связи, из которых оставляются только существенные. Связи представляются формально в виде чисел и параметрически заданных функций. Представленные в виде существенных связей являются одновременно основными линиями технического взаимодействия для коллективов, участвующих в разработке большой системы и объекта, входящего в ее состав и ее подсистемы.

3. Предполагается существование разработчика уровня n+1 и все подсистемы, с которыми можно установить контакт с целью установления существенных связей, описания идущим по ним взаимодействиям и формирование частных критериев эффективности для уровня n. Точно такие же функции разработчик уровня n выполняет по отношению к уровню n-1. Следует также выделить и учитывать вид связей, когда объект уровня n входит в большую систему через ее уровень n+1 и одновременно связан через свои характеристики и параметры с взаимодействующей и обслуживающей большой системой другого класса, не принадлежащей системе, в которую входит проектируемый объект.

4. После проведении процедур 2 и 3 разработчик системы обособлится внутри системы заданных параметров связи и согласованных критериев и может вести работу самостоятельно, зная детально свой уровень и только за него неся ответственность. Он выполняет оптимизацию проектируемого объекта по выделенным частным критериям, используя параметры по существенным связям как ограничение задачи.

Следует отметить, что аппарат существенных связей позволяет разрешить споры между соразработчиками.

Система, размещенная на уровне иерархии n, задается вектором своих проектных параметров и содержит систему уравненя n-1, которая задается вектором параметров K^n-1 .

Кроме этого, считаются известными операционные модели, с помощью которых устанавливается связь варируемых параметров с критериями соответствующего уровня иерархии.

Wⁿ = Wⁿ(Kⁿ, W^n-1(K^n-1))

Предположим, что на каждом уровне иерархии есть своя модель операции для установления связи варируемых параметров К данного уровня с показателями эффективности данного уровня.

Kⁿ

Wⁿ

K^n-1

W^n-1

Kⁿ⁺¹

Wⁿ⁺¹

bⁿ⁺¹

уровень n+1

kⁿ⁺¹ є Kⁿ⁺¹

уровень n bⁿ

kⁿ⁺є Kⁿ⁺¹

уровень n-1

b^n-1 ;k^n-1 є K^n-1

За полезный эффект уровня n-1 Wⁿ подсистеме n-1 приходится платить ресурсами затрат системе уровня n-1. Представим эти затраты вектором Sⁿn-1. В общем случае в состав вектора Sⁿn-1 входят компоненты массы, объема, энергии.Эти числовые ограничения, задаваемые в виде вектора Sⁿn-1, вносят дополнительные ограничения на возможность выбора вектора параметров на уровне n и им можно придать вид функции ограничений

gⁿn-1(Kⁿ )≥ Sⁿn-1

Обычно связь Sⁿn-1 можно рассматривать как существенную между уровнями n и n-1. Но одновременно Sⁿn-1 можно рассматривать как ресурс выделенной разработчиком системы n и для уровня системы n-1 можно выделить следующие ограничения:

gⁿn-1(K^n-1 )≤ Sⁿn-1

Таким образом, используя схему существенных связей между тремя уровнями, изображенных на рис.1, можно записать следующие ограничения:

gⁿ⁺¹n(Kⁿ⁺¹ )≥ Sⁿn-1 ≥gⁿn+1(Kⁿ ) (2)

gⁿn-1(Kⁿ )≥ Sⁿn-1 ≥g^n-1n (K^n-1 )

При этом считается, что S_nⁿ⁺¹ ≥S_n-1ⁿ ≥S_n-2^n-1 … ≥S₀ⁿ⁺¹ .

Помимо этого на каждом уровне иерархической системы существуют ограничения, не имеющие отношения к существующим связям внутри системы. Эти ограничения налагаются связями со взаимодействующими системами и имеют вид:

g_nⁿ (Kⁿ )≤bⁿ (3)

Каждое из ограничений (2) и (3) выделяет свое допустимое множество значений параметров Кⁿ,которое определяется следующим условием:

K_n-1ⁿ(S_n-1ⁿ)={Kⁿ|g_n-1ⁿ(Kⁿ)≥S_n-1ⁿ}

K_n+1ⁿ(S_nⁿ⁺¹)={Kⁿ|g_n+1ⁿ(Kⁿ)≤S_nⁿ⁺¹} (4)

K_nⁿ(b_nⁿ)={Kⁿ|g_nⁿ(K (ⁿ)≥bⁿ}

В выражении (4) I множество выделено связями с уровнем ( n-1), II множество- ограничениями, идущими от уровня (n+1),последнее- ограничениями на уровне (n). Пересечение этих трех множеств образует общее допустимое множество Kⁿ на уровне (n):

Kⁿ= K_n-1ⁿ(S_n-1ⁿ)Λ K_n+1ⁿ( S_nⁿ⁺¹)Λ K_nⁿ (bⁿ)= Kⁿ(S_n-1ⁿ, S_nⁿ⁺¹, bⁿ) (5)

Тогда задача поиска оптимального решения к_nⁿє K_nⁿ при фиксированных параметрах связи S ставится в следующей форме:

Найти: Kⁿ(S_n-1ⁿ, S_nⁿ⁺¹, bⁿ)=argmax Wⁿ(Kⁿ,W^n-1( K^n-1))

kⁿєKⁿ

Плата за наличие подсистемы уровня (n-1) и за принадлежность к надсистеме уровня (n+1) выразилась для допустимого множества конструктивных параметров уровня (n) в сжатии допустимой области решения от исходной K_nⁿ( bⁿ) до Kⁿ.

Далее в задаче синтеза параметры существенных связей S варьируются , параметры b считаются фиксированными. На каждом иерархическом уровне, начиная с нижнего l=0, l=0,n , найдем связь максимального показателя эффективности W_M^l подсистемы уровня (1)с параметрами существенных связей:

l=0:W_M⁰(S₀¹, b⁰)=max W⁰(K⁰) (6)

k⁰ єK⁰(S₀¹, b⁰)

l=1: W_M¹(S₁²,S₀¹,b¹, b⁰)=max W¹(K¹) (7)

k¹ єK¹(S₀¹,S₁²,b¹, b⁰)

l=l :W_M¹(S₀¹,S₁²,…S_l-1^l,S_l^l+1, b⁰… b^l)=max W^l(K^l) (8)

k^l єK^l(S₀¹,S₁²,…S_l^l+1, b⁰… b^l)

l=n :W_Mⁿ(S₀¹,S₁²,…S_nⁿ⁺¹, b⁰… bⁿ)=max Wⁿ(Kⁿ) (9)

kⁿ єKⁿ(S₀¹,S₁²,…S_nⁿ⁺¹, b⁰… bⁿ)

Опираясь на соотношения (6)-(8) и назначая параметры существенных связей S, можно управлять процессом синтеза многоуровневой системы в целом и ее отдельных подсистем. Если считать, что при проектировании мы ограничиваемся уровнем n и для системы W_n это ее глобальный критерий, то W_Mⁿ определяется:

_ _

W_MМⁿ(b⁰…bⁿ)= max W_Mⁿ(S₀¹…S_nⁿ⁺¹,b⁰…bⁿ) (10)

S₀^1,,S₁²,…S_nⁿ⁺¹

_ S- оптимальное знаение существенных связей.

Результатом решения задачи (10) являются оптимальные значения параметров связей всех _ _

уровней S₀¹... S_nⁿ⁺¹. Подстановка этих параметров в соотношения (6)-(9) позволяет получить для

_ _ каждой подсистемы показатели эффективности подсистемы каждого уровня W_MM¹(S₀¹…S _l^l+1,b⁰…b^l), l=0,n, соответствующие максимальные показатели эффективности выражения (10) и в точках максимума найти конструктивные параметры подсистемы k^lєK^l, соответствующие оптимальному построению всей системы, т.е. :

_ _

K_MM^l=arg W_MM^l(S₀¹,…S_l^l+1,b⁰,…bⁿ) (11)

Координация в многоуровневых иерархических системах.

Цель подсистемы более высокого иерархического уровня влиять на подсистемы более низких иерархических уровней таким образом, чтобы достигалась общая цель, заданная для всей системы. Это и составляет содержание понятия координация. При решении задачи координации рассматриваются следующие вопросы:

1. Установление правил, определяющих действие подсистем (эти вопросы решаются при формировании структуры системы).

2. Практическое обеспечение этих правил при функционировании системы.

Проблем координации в многоуровневой системе с достаточной общностью можно рассмотреть на пример двухуровневой системы, так как при синтезе более общей многоуровневой системы ее можно использовать в качестве основного модуля. Рассмотрим общую блок-схему двухуровневой системы:

C₀

C₁

C_i

C_n

Процесс Р P₁ Pi P_n

ω_n

γ₁ ω₁ γ_i ω_i γ_n

m₁ z₁ m_i z_i m_n z_n

ξ Y

Рис.1

Система, изображенная на рис.1, имеет (n+2) основных подсистем: вышестоящую управляемую систему С₀,n- нижестоящих управляемых систем и управляемый процесс Р.В системе существует два вида вертикального взаимодействия между подсистемами: передача вниз командных сигналов γ_i , которые называются координирующими, сигналы от нижестоящих управляемых систем к процессу Р m_i , i=1,n, сигналы обратных связей от нижестоящих управляемых систем к С₀ ω_i, i=1,n и от процесса Р к системам С_i, i=1,n z_i.

Процесс Р представляет управляемую систем и нему подходят входные сигналы двух видов: управляемые сигналы m_iєM, i=1,n от систем управления нижнего уровня C₁…C_nи сигналы возмущения ξєξ от окружающей среды.

Символом Y отображается выход процесса Р.

Рассмотрим i-ую систему управления С. К системе С_i поступают входные сигналы двух видов: координирующий сигнал γ_iє γ, поступающий от вышестоящей управляемой системы С₀ и информационный сигнал z_{i ,} i=1,n, т.е. сигнал ОС , поступающий от процесса. Выходом С_i является локальное управление m_i, выбираемое из М, и сигналы ОС ω_i. Управляемую систему С₀ будем называть координатором, так как ее выходные сигналы γ_i являются координирующими для систем С₁…С_n. Для формирования координирующих сигналов используют информацию ωєω, получаемую посредством ОС от нижестоящих управляемых систем: ω- множество информационных сигналов. Сигналы ОС z_i, поступающие на вход локальной управляемой системы С_i . содержат информацию относительно поведения процесса Р и связаны функциональной зависимостью с управляющим сигналом m, внешним возмущением ξ и выходом вышестоящую управляемую систему С₀ и содержит в себе информацию относительно поведения нижестоящих управляемых систем. Следовательно, множество ω является функцией координирующего сигнала γ, информационных сигналов ОС z_i , i=1,n,получаемых нижестоящими управляемыми системами и их управляющих воздействий m.

Относительно указанных взаимодействий межу подсистемами сделаем два допущения:

1. В явном виде не предусматривается прямая коммуникация между нижестоящими управляемыми системами: информация от подсистемы С_i к подсистеме С _n передается через С_0.

2. Вышестоящая система С₀ непосредственно не взаимодействует с процессом, а осуществляет взаимосвязь через подсистемы С_i.