Глава 2. Статически неопределимые конструкции
2.1 Расчет конструкций методом сил
Пример 1. Требуется рассчитать конструкцию (рис. 52).
Решение.
- Определение степени свободы конструкции
.
Это говорит о наличии 2-х избыточных связей.
- Основная система для расчета получается удалением 2-х связей. Необходимо помнить о безусловно необходимых связях (их нельзя удалять) и условно необходимых, которые можно удалить.
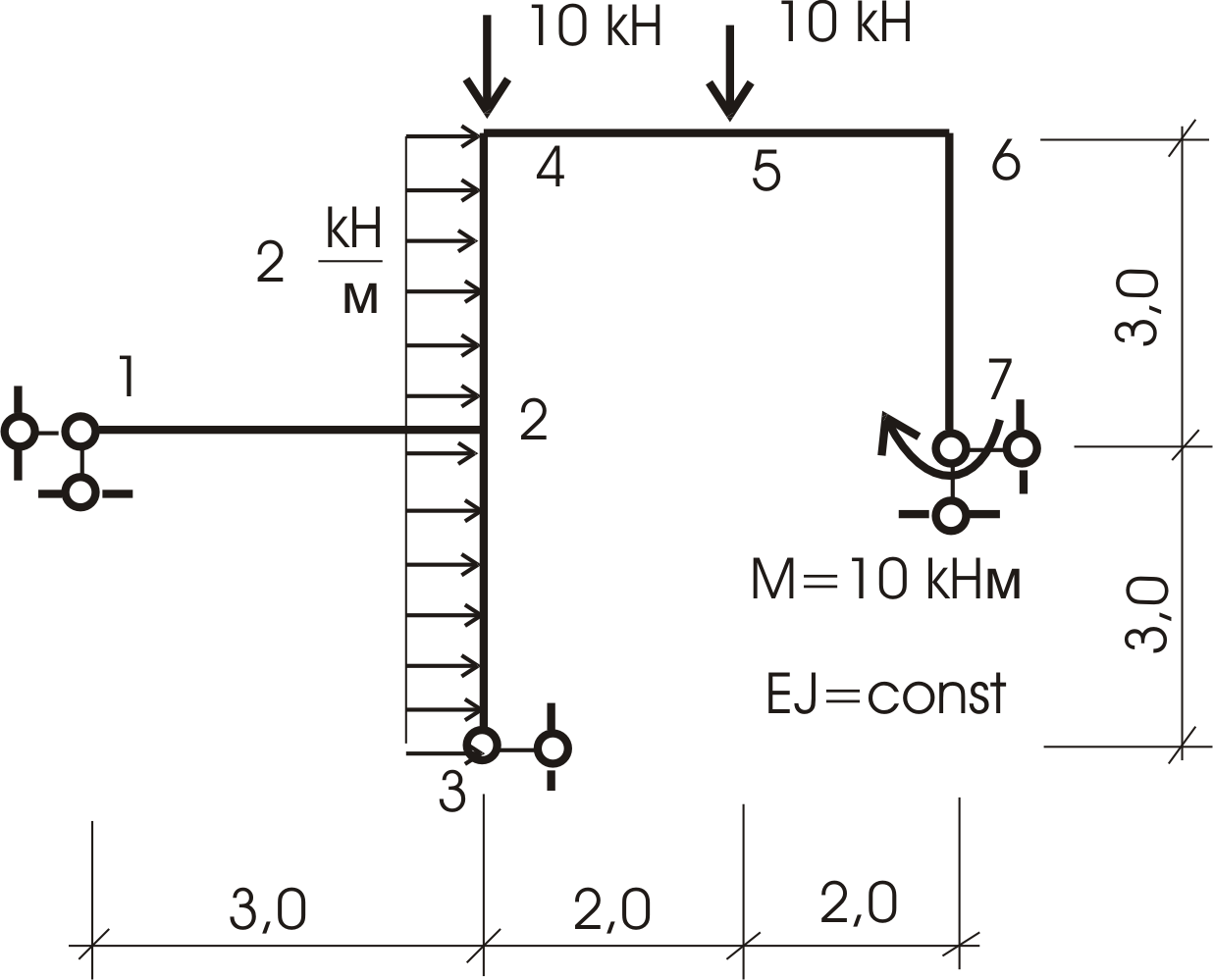
Рис. 52
Варианты основной системы приведены на рисунке 53. Варианты в) и д) использовать в дальнейших расчетах, как уже написано, нельзя, т. к. удалены безусловно необходимые связи и получаемая основная система мгновенно изменяемая!
Привычна по виду схема б), но оптимальной для дальнейшего расчета будет схема г). Примем ее за основную систему.
- Для основной системы запишем уравнения совместности деформации или канонические уравнения:
;
.
Каждое из этих уравнений гласит: суммарное перемещение точки приложения неизвестных усилий по их направлению от воздействия всех сил, действующих на конструкцию, равно нулю.
Здесь
- перемещение точки приложения i-ой
неизвестной по ее направлению от
воздействия к-ой силы
;
- перемещение точки приложения i-ой
силы по ее направлению от воздействия
на конструкцию внешней нагрузки.
Для определения
этих коэффициентов и грузовых слагаемых
строим эпюры изгибающих моментов от
сил
и от внешней нагрузки (рис. 54).
Вычисляем
:
.
Эпюру М1 перемножаем саму на себя:
.
Вычисляем
.(Перемножаются
эпюры М1 и М2 ):
.
Вычисляем
.
(Перемножается эпюра М2
сама на
себя):
.
Вычисляем
.
(Перемножаются эпюры М1
на МР
):
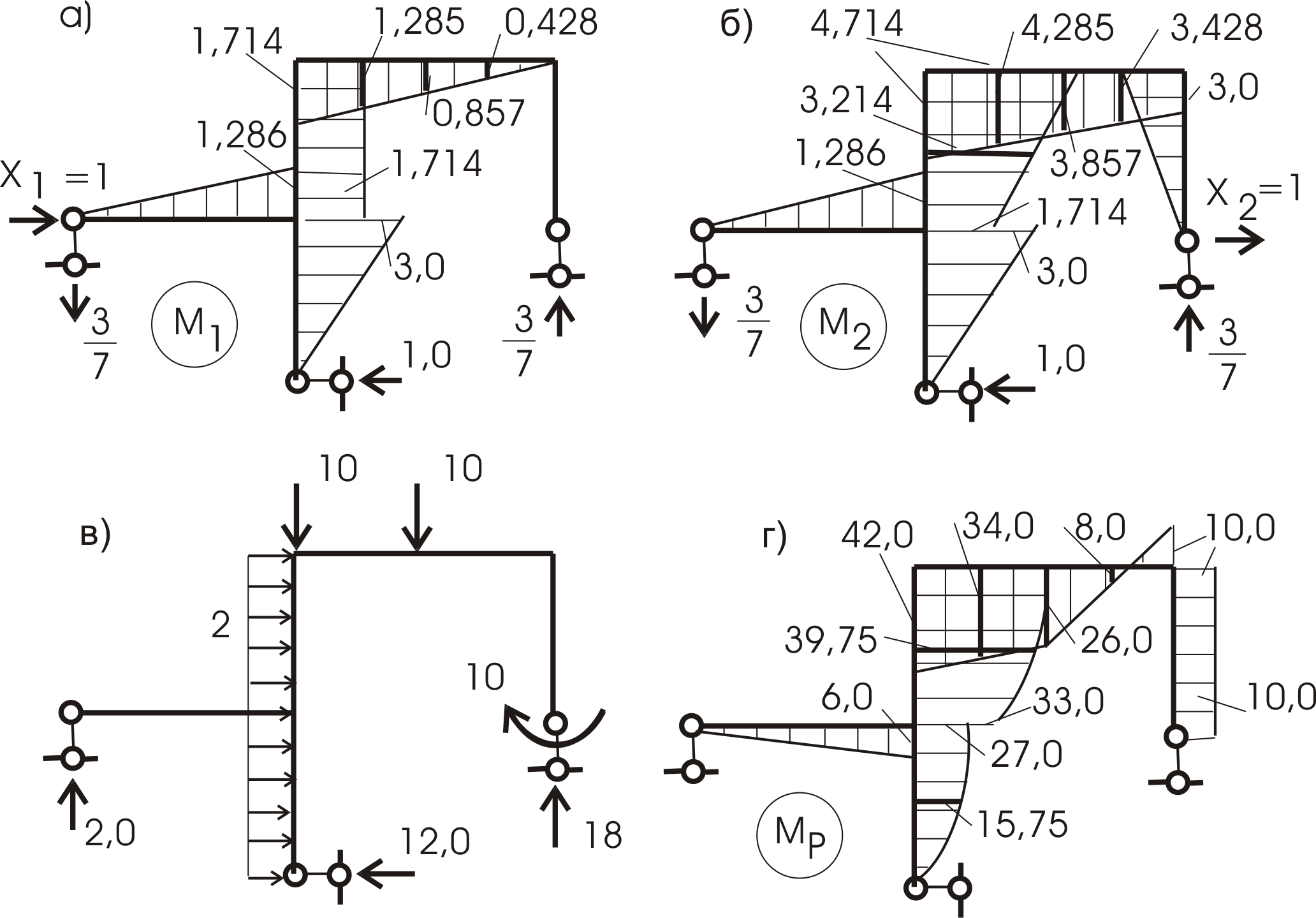
Рис. 54
.
Вычисляем
.
(Перемножаются эпюры М2
на МР
):
.
- Решение системы:
х1=
- 12,155 кн;
х2=
- 2,368 кн.
- Построение эпюр внутренних усилий для заданной рамы.
1-ый путь построения
К основной системе (рис. 55) приложим заданную нагрузку и найденные усилия в отброшенных связях с учетом их знака. Для полученной схемы строим эпюры внутренних усилий обычным путем (методами сопротивления материалов).
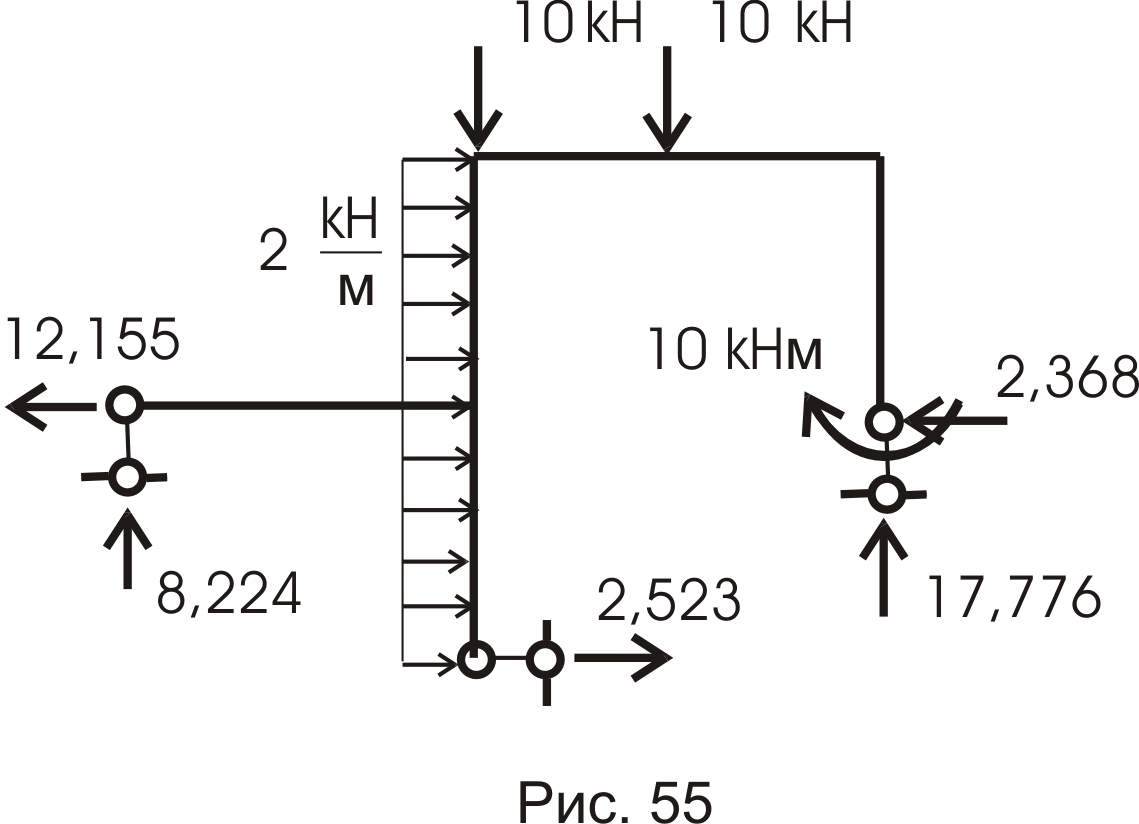
Определяем реакции в связях:
; 
.
кн.
; 
.
; 
.
.
(кн).
Тогда
из второго уравнения
кн.
Эпюры внутренних усилий М, Q и N показаны на рисунке 56(а,б,в). Читателю предлагается самостоятельно построить их и результаты сравнить.
- Производим статическую проверку – равновесие узла должно сохраняться (рис. 56г,д).
; 
,
.
; 
,
.
; 
, 
.
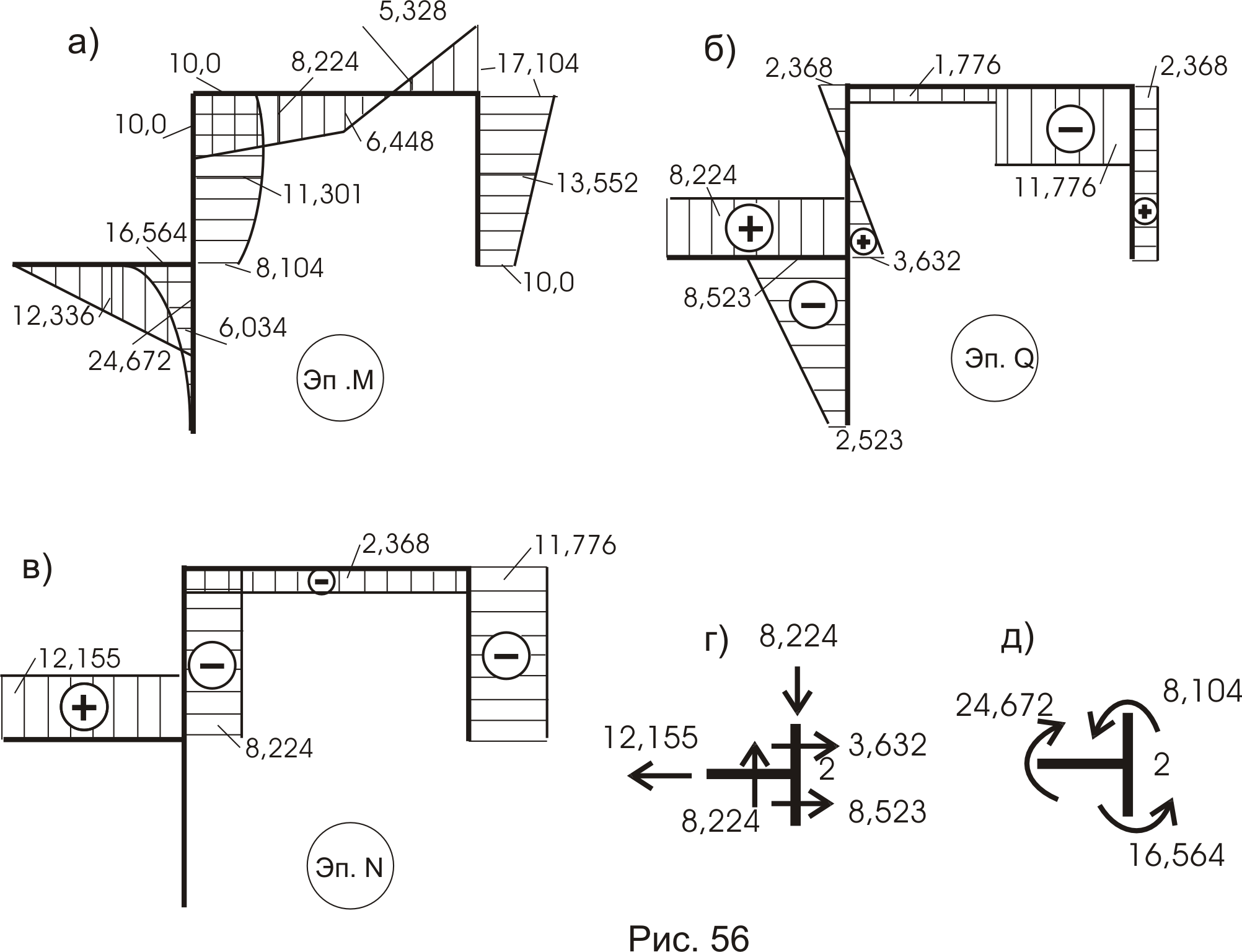
- Кинематическая проверка.
,
где
- одна из единичных эпюр
.
Перемножим
(рис.56а) на
(рис. 54а):
Процент погрешности составит:
.
2-ой путь построения
Он основан на принципе независимости действия сил (рис. 57).
.
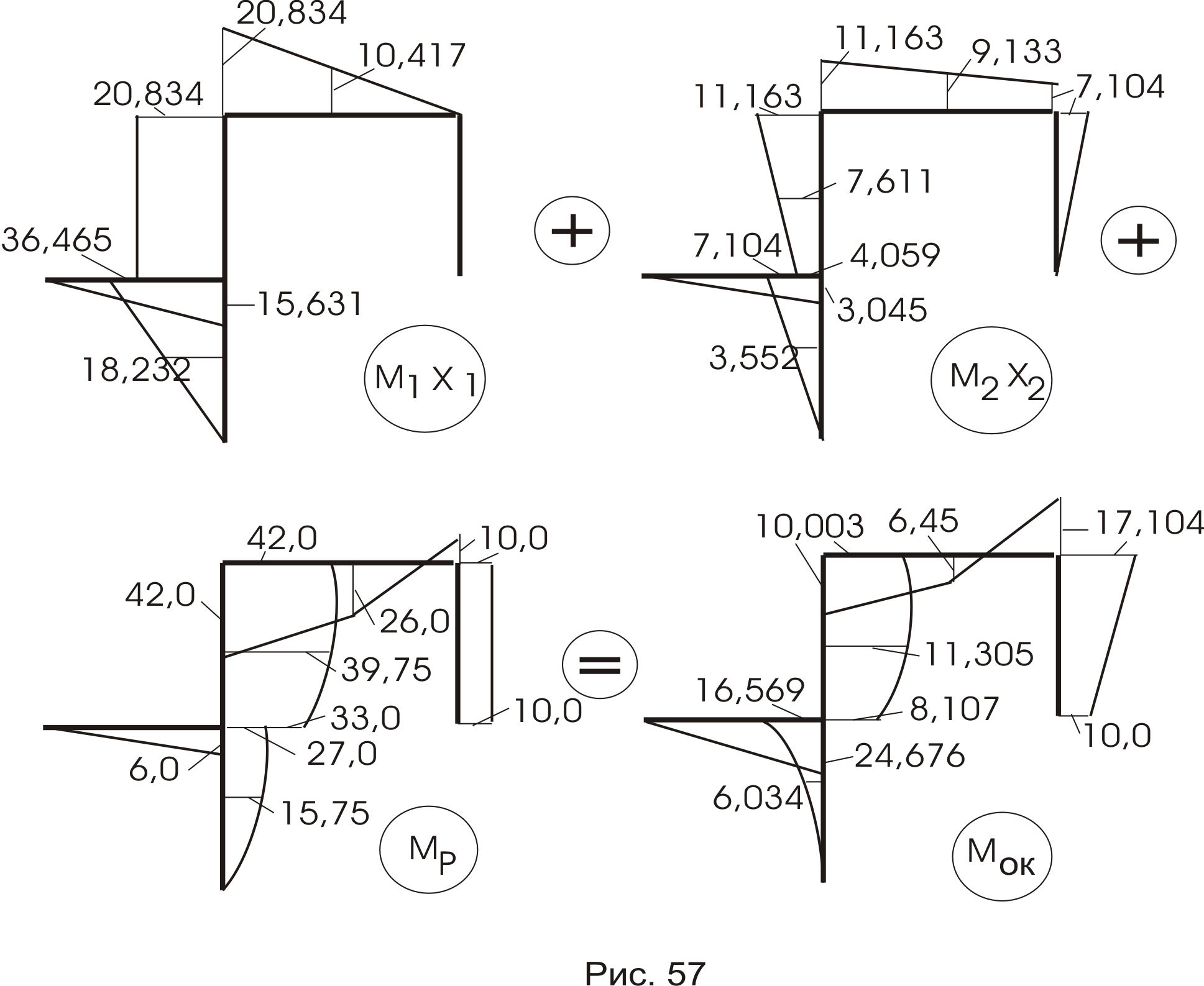
Сравнивая полученные результаты, по мы видим небольшие погрешности вычисления. Следуя дальше вторым путем, эпюру Qоk строим по эпюре Мок. Для этого нашу раму расчленим на отдельные элементы (балки): 1 – 2; 2 – 3; 2 – 4; 4 – 6; 6 – 7, т. е. на 5 отдельных балок (рис.58). Загружаем их внешней нагрузкой и моментами в жестких узлах, взятых из эпюры Мок (рис.57).
Разберем одну из балок, скажем, балку 2 – 4 (рис. 58в). Для удобства расположим ее горизонтально (рис. 58е).
Определяем опорные реакции
; 
. 
кН.
;
.
; 
.
(кН).
(кН).
По этим данным строим эпюру Q (рис. 58е).
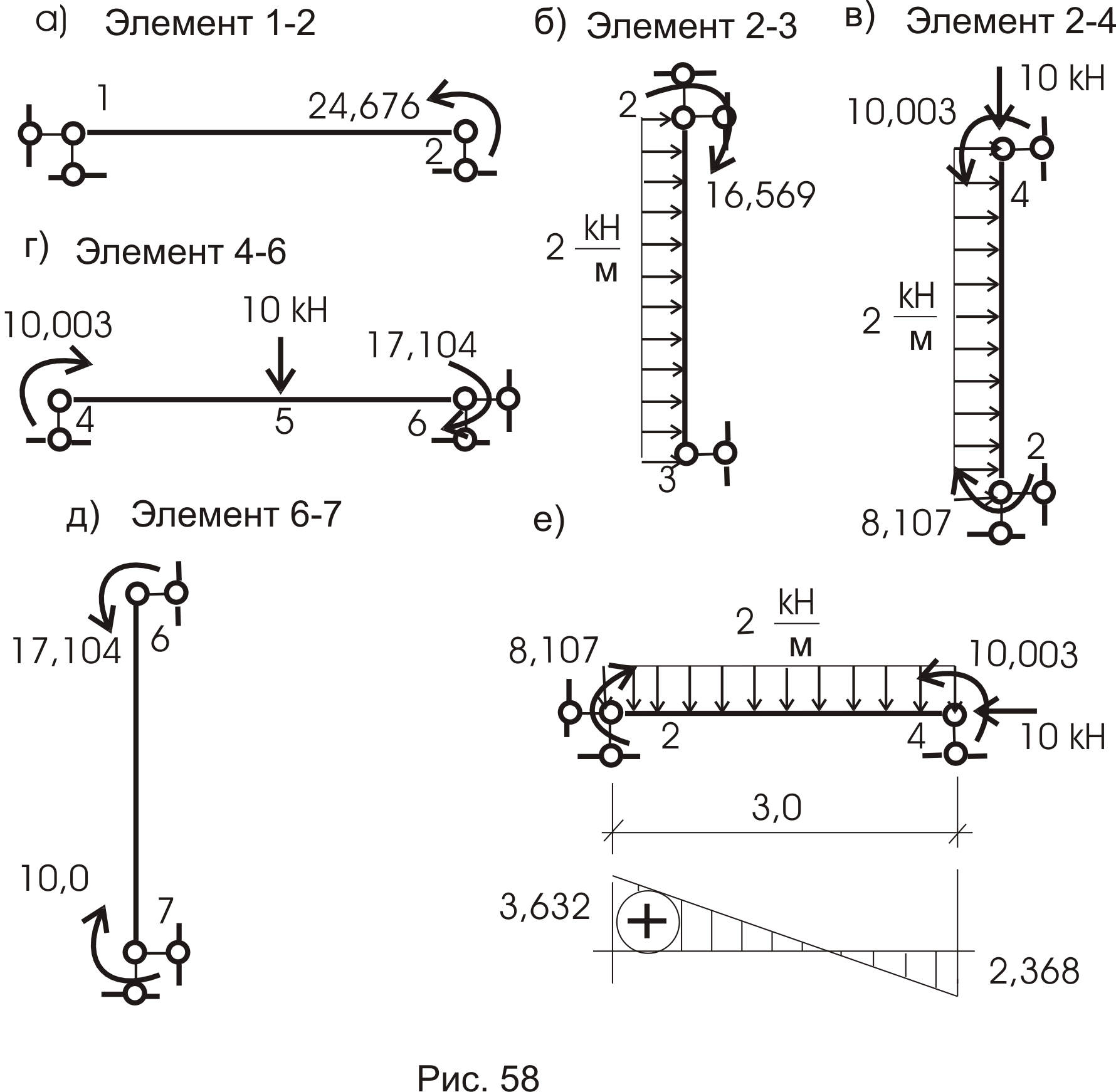
Сравнивая значения и знаки (!) с эпюрой Qok, построенной ранее
(рис. 52), на этом участке мы видим полное совпадение.
Эпюру Nok строим по эпюре Qok, используя способ вырезания узлов, как это делалось в статической проверке, где мы показали это на примере одного узла. Используя результаты Qок, построенной ранее, покажем на примере узла 4 определение продольных усилий в стержнях 4 – 2 и 4 – 6 (рис. 59).
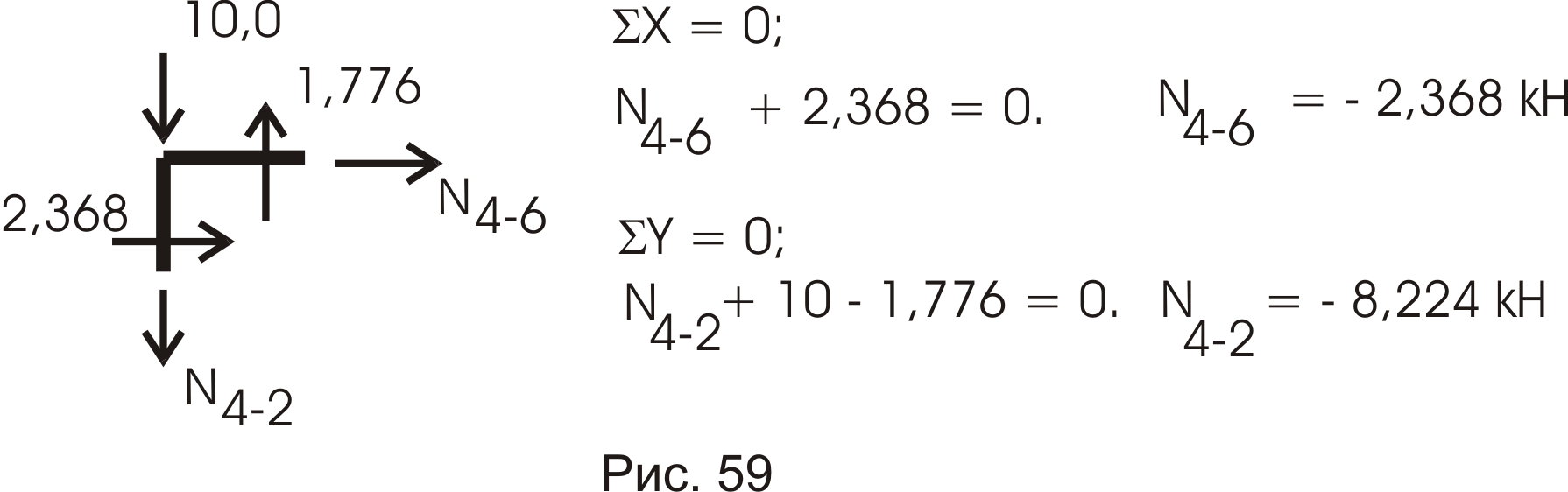
Cверим
значения
и
со значениями, найденными ранее (рис.
56) – они полностью совпадают.
Приведем пример расчета рамы без пояснений (рис. 60).
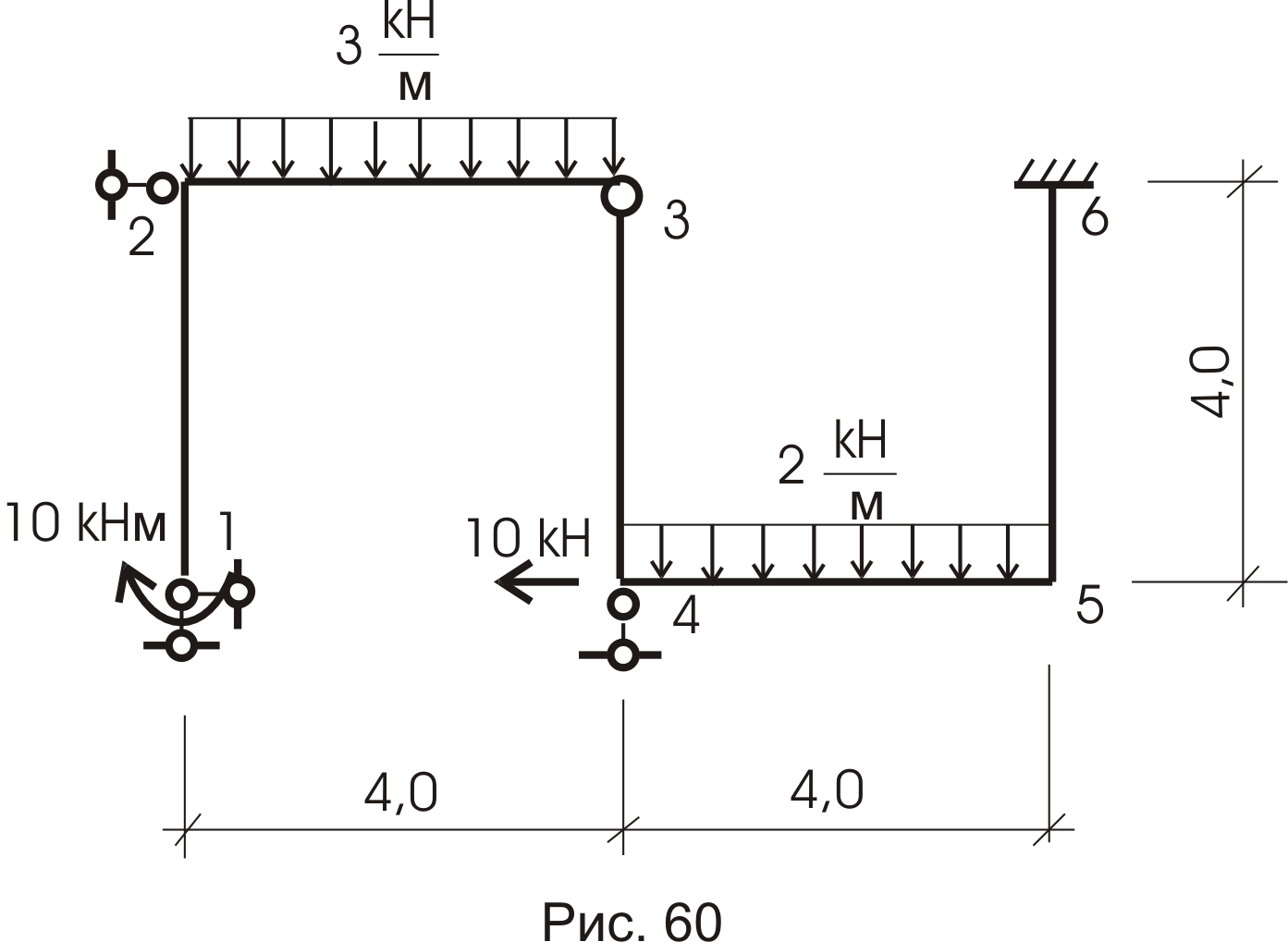
1.
.
2. На рисунке 61 приведены варианты основных систем.
Делаем выбор на варианте а).
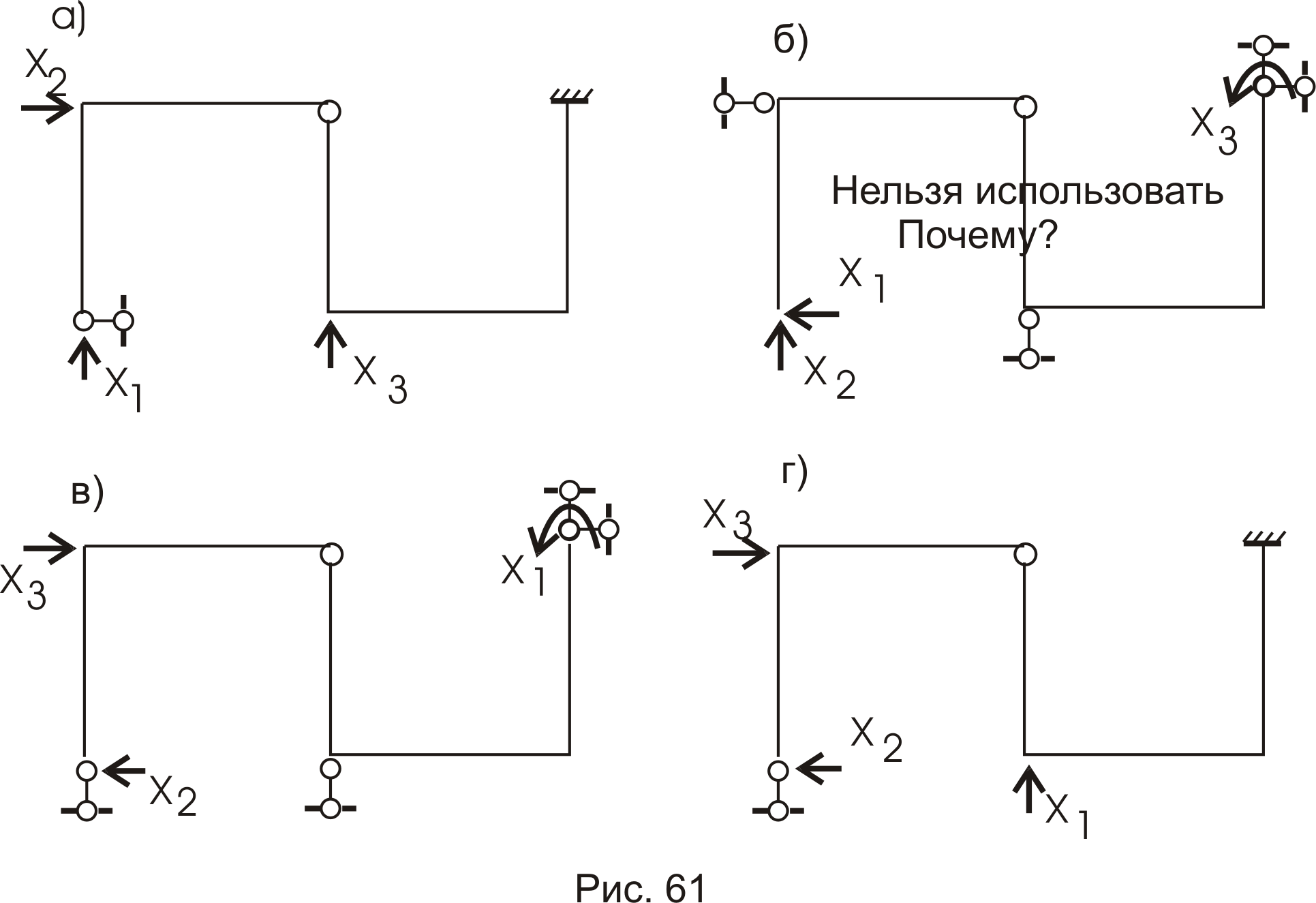
3.
;
;
.
;
;
;
;
;
;
;
;
.
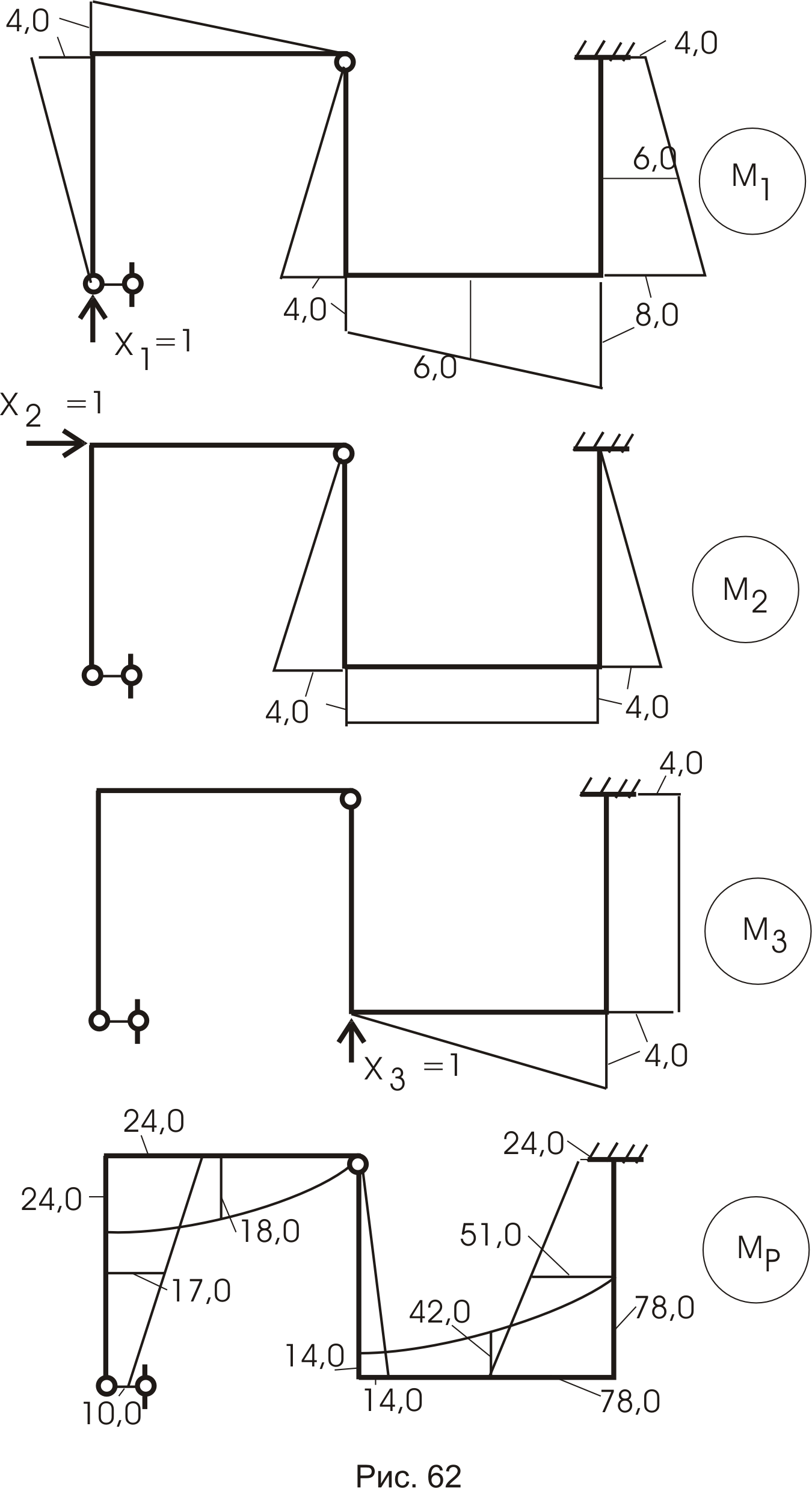
Проверили? Все правильно?
Система уравнений:
;
;
.
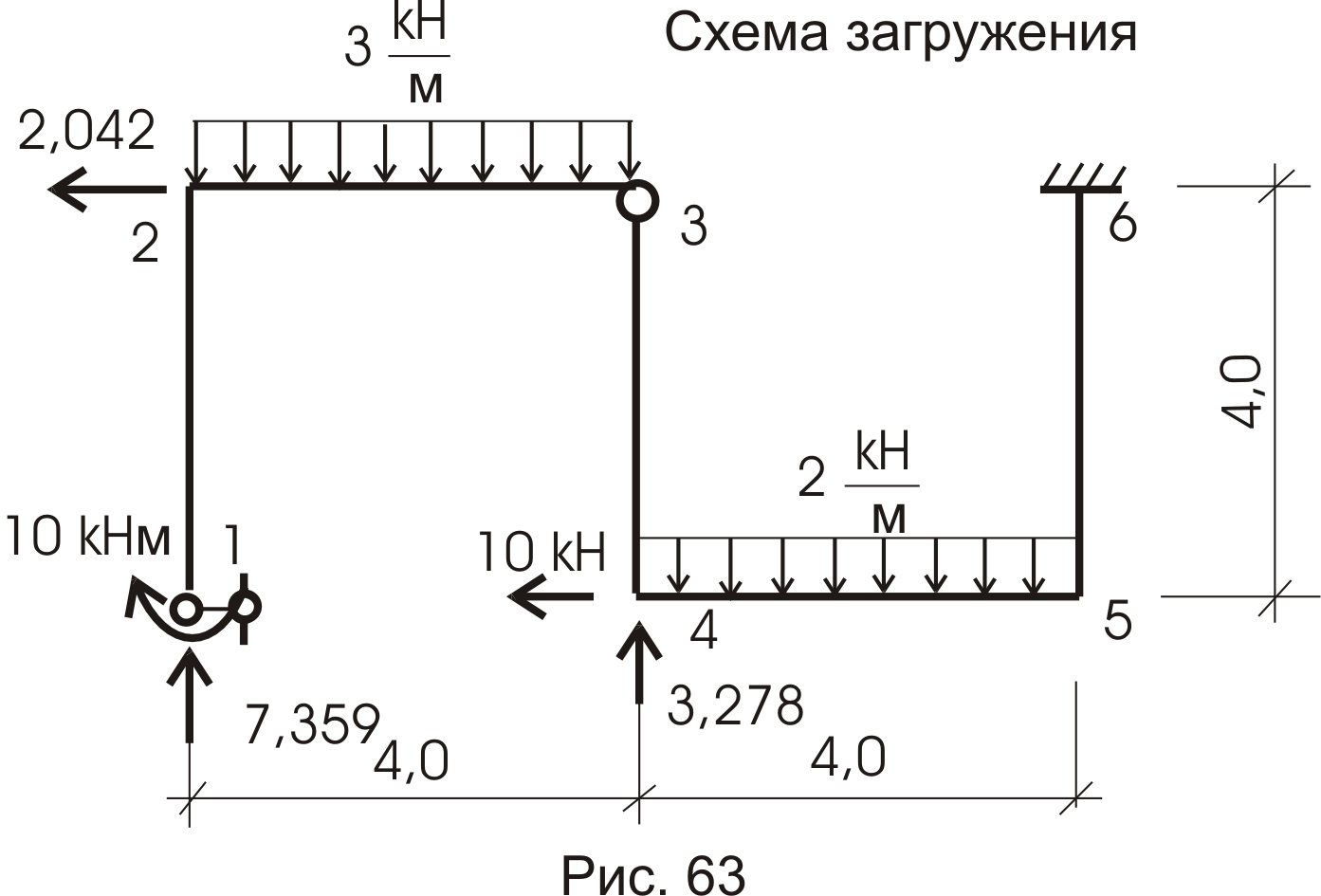
Получаем: 
кН
;
кН; 
кН.
Загружаем конструкцию найденными усилиями и внешней нагрузкой (рис. 63). Окончательные эпюры внутренних усилий приведены на рисунке 64.
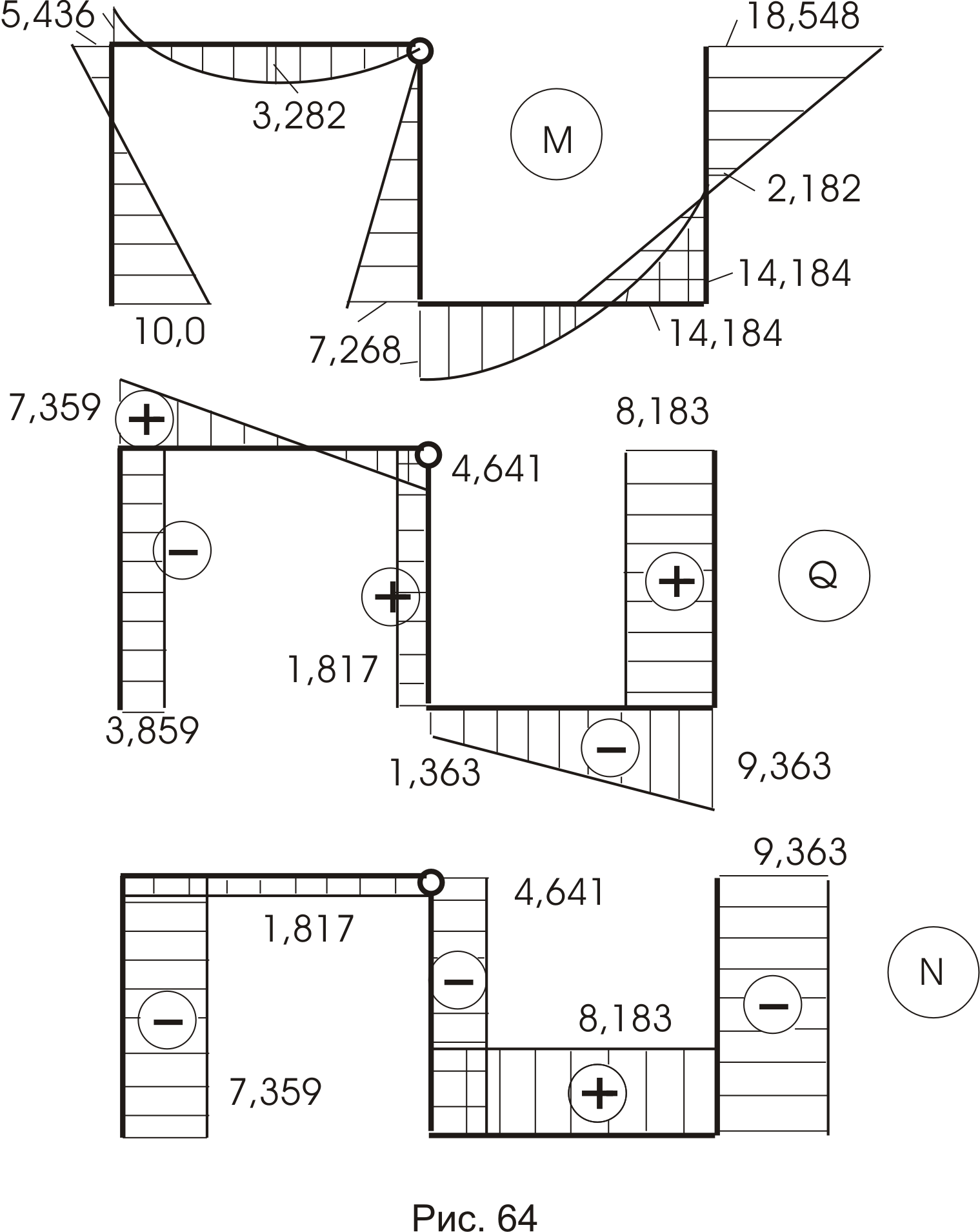
Статическая проверка.
По моментам видно (из эпюры М – рис. 64 -все узлы в равновесии. По Q и N рассмотрим характерные узлы (рис. 65а,б). Видим, что уравнения статики соблюдаются.
Кинематическая проверка.
.
Погрешность составляет 0,04%.
Пример расчета статически неопределимой балки
Для балки (рис. 66а) определим внутренние усилия.
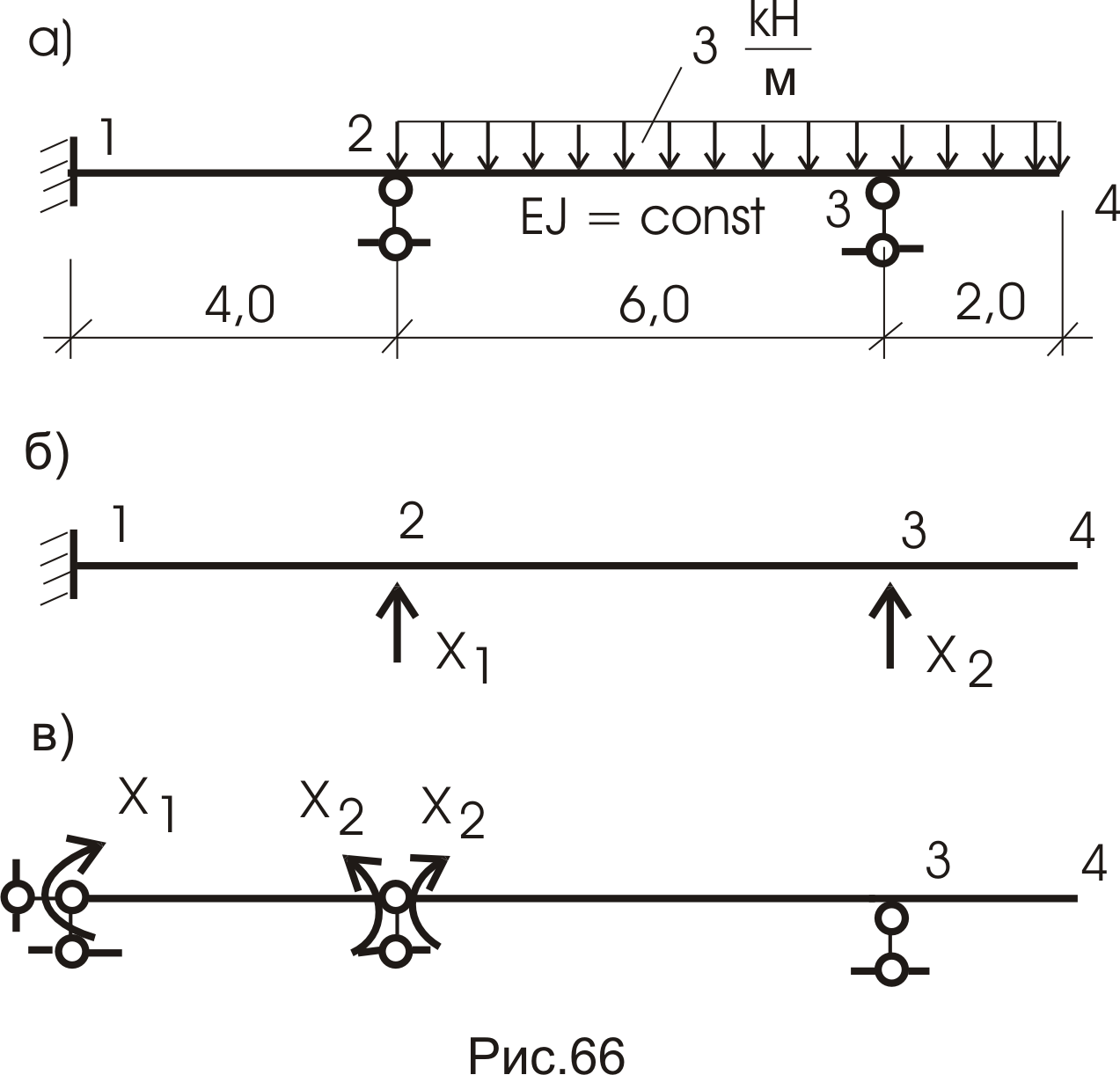
Решение.
1)
.
Два раза статически неопределимая балка. Основные системы метода сил представлены на рисунке 66 б,в.
Для расчета примем вариант в).
2) Запишем систему канонических уравнений:
;
.
3) Вычисляем
коэффициенты
и
.
Эпюры от единичных загружений представлены на рисунке 67б,в) и от внешней нагрузки - на рисунке 67г.
;
;
;
;
.
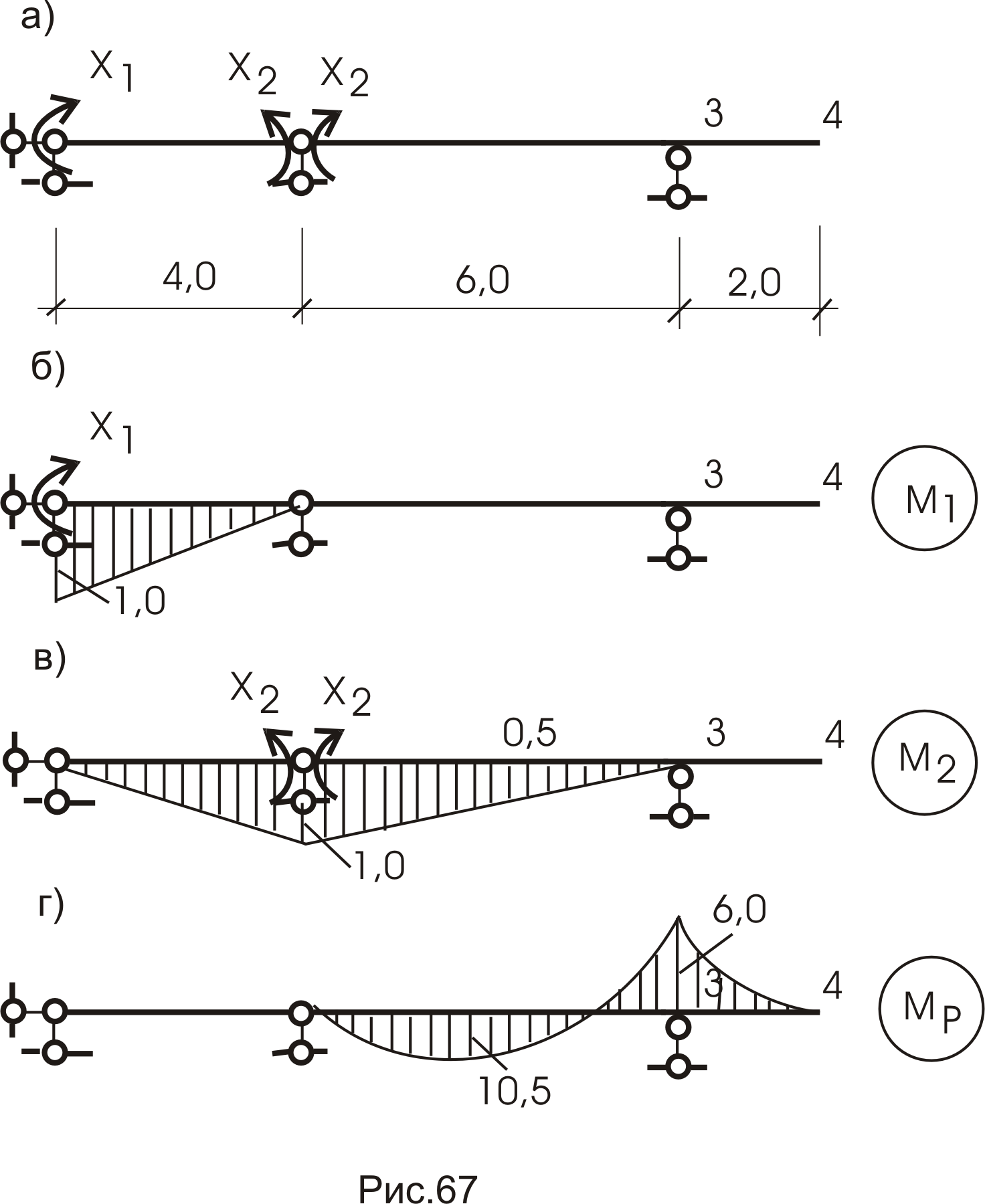
Решение системы:
;
.
Дает
кнм;
кнм.
По полученным
значениям строим
и
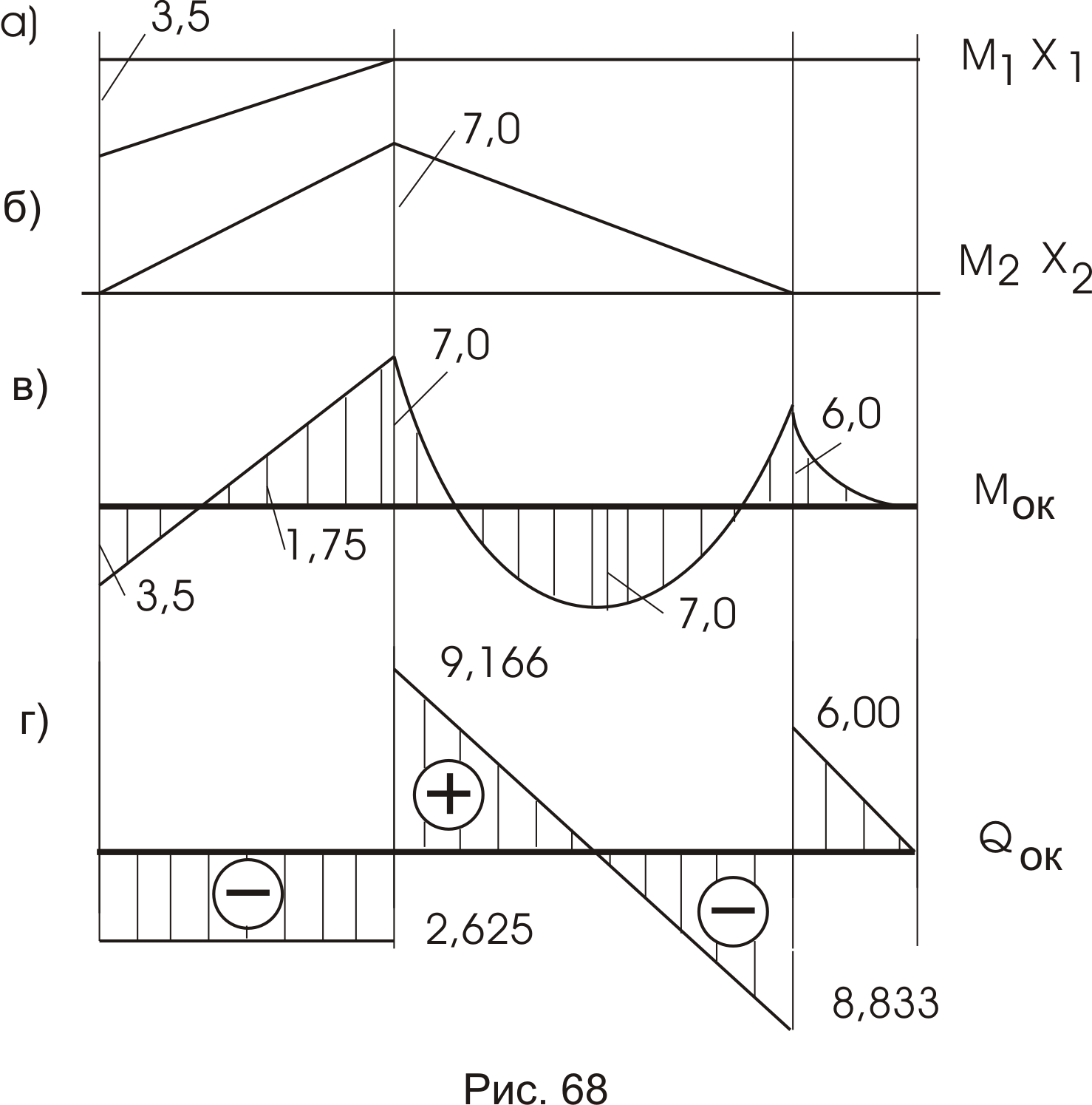
(рис. 68а,б)
и
(рис. 68в).
Проверки.
а) Статическая проверка. Значения моментов на опорах (рис. 68в) одинаковы и равновесие обеспечивается. Проверка удовлетворяется.
б) Кинематическая проверка.
Перемножим
с
.
Проверим, будет ли взаимный угол поворота
сечений балки на опоре 2 равен нулю?
.
Проверка удовлетворяется.
Эпюра
строится по эпюре
по рассмотренному ранее принципу.
Выполните построение самостоятельно
и свой результат сверьте с приведенным
решением на рисунке 68г.
2.2 Расчет неразрезных балок
Для балок с большим числом пролетов (неразрезные балки – рис. 69а) оптимальная основная система получается введением шарниров во все опорные узлы (как это мы сделали для разобранной выше балки – рис. 66в). На полученной основной системе (рис. 69б) направление неизвестных моментов показаны на трех опорах, входящих в общее уравнение.
Для неразрезных
балок неизвестные обозначаются через
- изгибающий момент на
ой опоре. Опуская доказательства,
распишем одно уравнение из системы
канонических уравнений для основной
системы (рис. 69б), скажем, для
- ой опоры при
:
.
Данное уравнение носит название - уравнение трех моментов.
В этом уравнении:
- длина пролета (пролет нумеруется по
номеру правой опоры);
и
- фиктивные реакции (
- правая реакция для
- го пролета;
- левая реакция для
пролета). Они получаются от нагрузки,
представленной эпюрой моментов
соответствующих пролетов, которые, в
свою очередь, строятся от заданного
загружения соответствующих пролетов.
Тогда левая часть системы канонических уравнений будет представлять собой ленточную матрицу вида (для шести неизвестных):
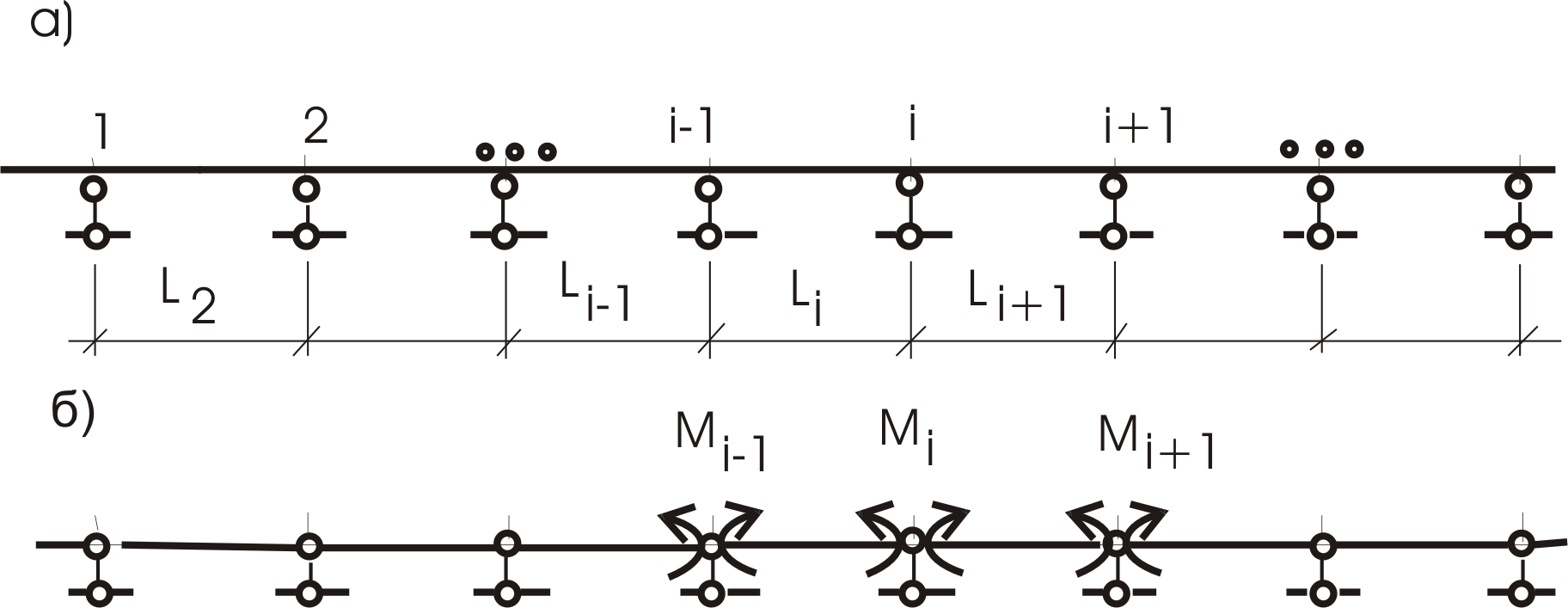
Рис. 69
.
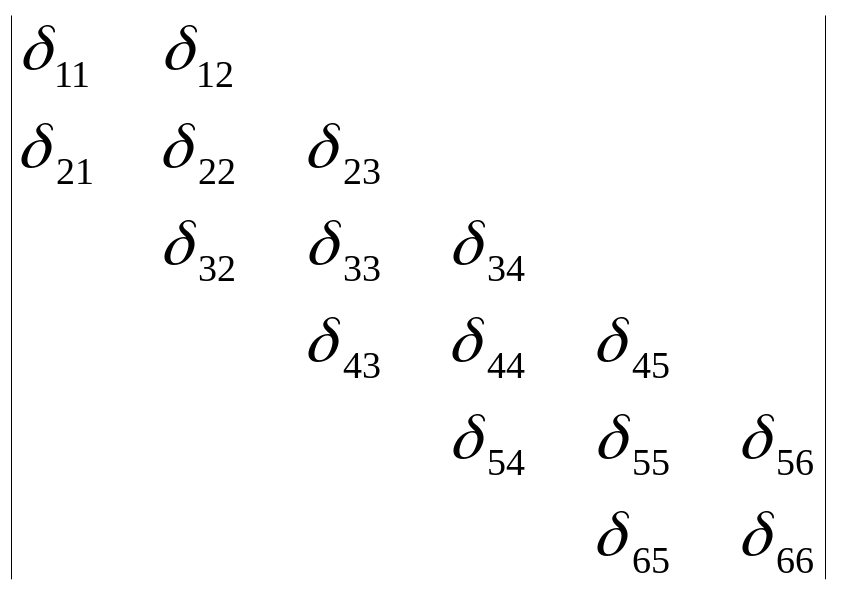Заметим, что уравнения (за исключением первого и последнего) содержат только три слагаемых.
Вернемся к балке, представленной на рисунке 66а.
Для получения основной системы примем следующие упрощения:
заделку заменим фиктивным пролетом, равным нулю;
консоль отбросим, но влияние нагрузки на консоли выразим (заменим) через опорный момент
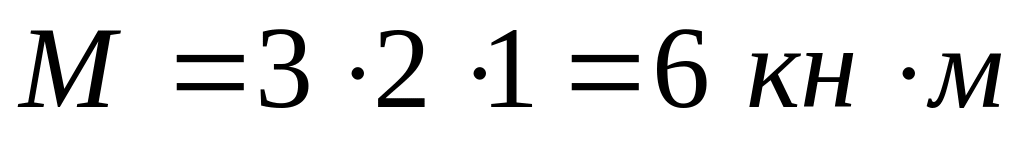и примем его со знаком минус, т. к. данный
момент растягивает верхние волокна, а
неизвестные опорные моменты, как видно
из основной системы, - нижние (рис. 70а).
Запишем уравнения трех моментов для каждого неизвестного момента. Для опоры 1:
.
Для опоры 2:
Упростим левую
часть уравнений, зная, что
и величину пролетов:
;
.
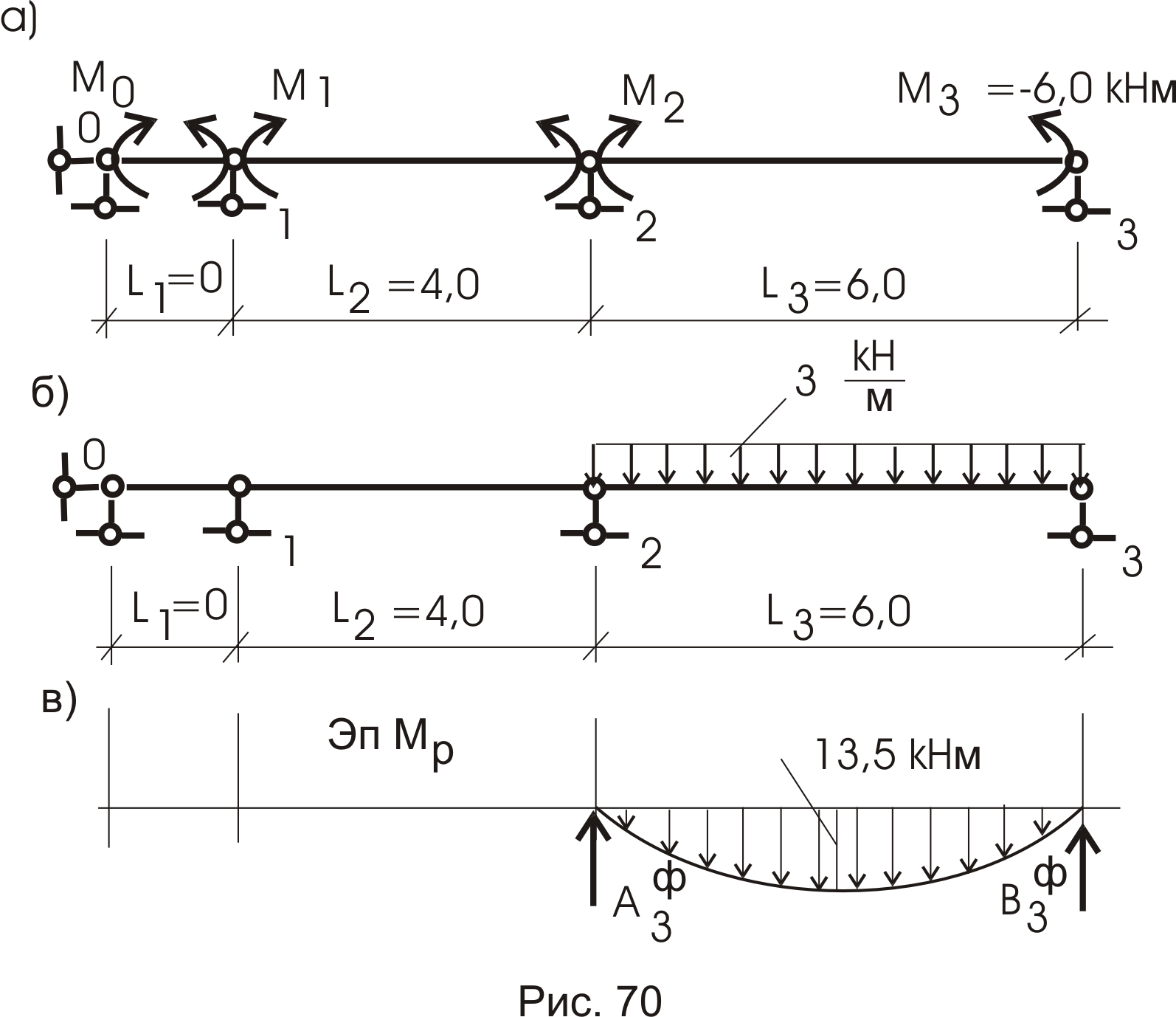
Для определения
загрузим основную систему внешней
нагрузкой (рис70б). Загружен третий пролет
равномерно распределенной нагрузкой,
от которой эпюра моментов представляет
собой квадратную параболу с ординатой
по середине
(кнм).
Эту эпюру моментов представляем в виде фиктивной нагрузки на третьем пролете (рис. 70в). От этой нагрузки вычисляем фиктивные опорные реакции:
(кнм2).
Учитывалась симметричность загружения (получаем величину реакций, как половину площади квадратной параболы).
На пролетах 1 и 2
нет нагрузки и поэтому
.
Вычисляем и правую часть уравнений:
;
или
;
.
Из первого уравнения находим:
тогда из второго определим:
и 
.
Сравнивая результаты с вычисленными обычным путем (рис.68в), видим их совпадение.
Рассмотрим следующий пример (рис. 71а).
1. Выбираем основную систему (рис. 71б).
2. Записываем уравнения 3-х моментов:
;
;
.
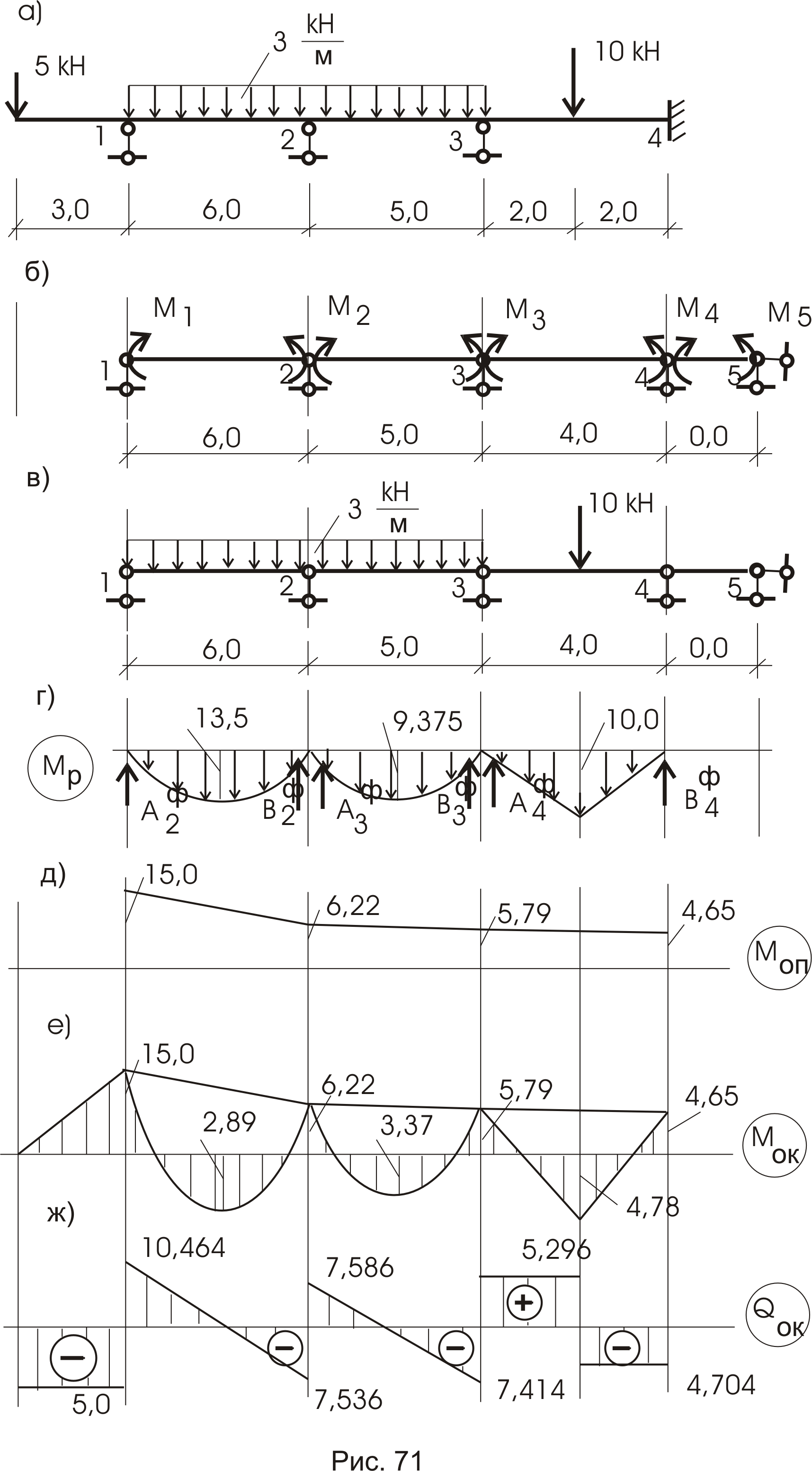
Для вычисления
и
построим эпюры изгибающих моментов в
основной системе от внешней нагрузки
(рис. 71в,г).
3. Вычисляем фиктивные реакции:
Второй пролет:
.
.
Третий пролет:
;
.
Четвертый пролет:
;
.
Подставим полученные значения в уравнения:
.
4. Решение системы дает:
.
5. Построение окончательных эпюр.
Эпюра изгибающих моментов.
В неразрезных
балках окончательная эпюра
(рис. 71е) строится путем сложения эпюры
(рис. 71г) и эпюры опорных моментов (рис.
71д).
Эпюра Qок строится уже известными приемами (рис. 71ж):
для балки 1 – 2:
;
(кн);
для балки 2 – 3:
;
(кн);
для балки 3 – 4
;
(кн).
Опорные реакции
определяются по эпюре
.
Можно использовать два подхода:
1) Используем
правило – в точке приложения сосредоточенной
силы на эпюре
наблюдается скачок на величину данной
силы. Отсюда:
2) Равновесие опорного узла.
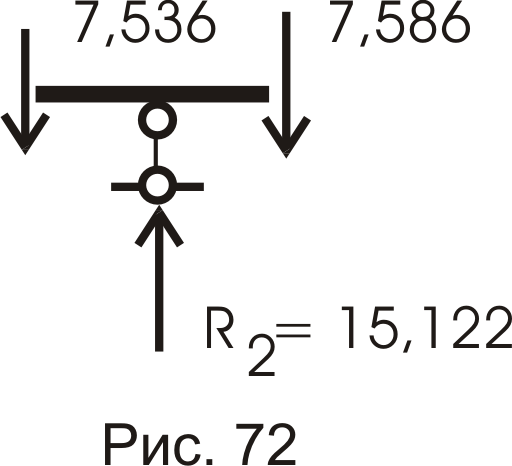
Вырезаем опорный узел (для примера – узел 2, рис. 72). В местах разреза появляются перерезывающие силы, их направляем с учетом знака. Тогда:
дает:
