Сечение 4 на участке 4 – 6.

Линия влияния Q_4-6 .

Величина усилия Q_4-6 вычисляется из условия равновесия нижней части (стержень 4-6):

.

Обратим внимание, что величина перерезывающей силы (Q_4-6) от положения силы Р = 1 не зависит, следовательно, (рис. 42д).

Линия влияния N_4-6 .

Усилие N_4-6 вычисляется как сумма всех сил на ось стержня, располагающегося ниже сечения 4 участка 4 - 6.

и, поскольку величина N_4-6 не зависит от координаты х, можем утверждать: (рис. 42е).

Линия влияния М_4-6 .

Изгибающий момент в сечении 4 участка 4 – 6 вычисляется:

и опять - таки не зависит от места расположения Р = 1. Таким образом, меняется так же, как и , но все ординаты л.в. Н₆ увеличиваются на 4 (м), т.е.. (рис.42ж).

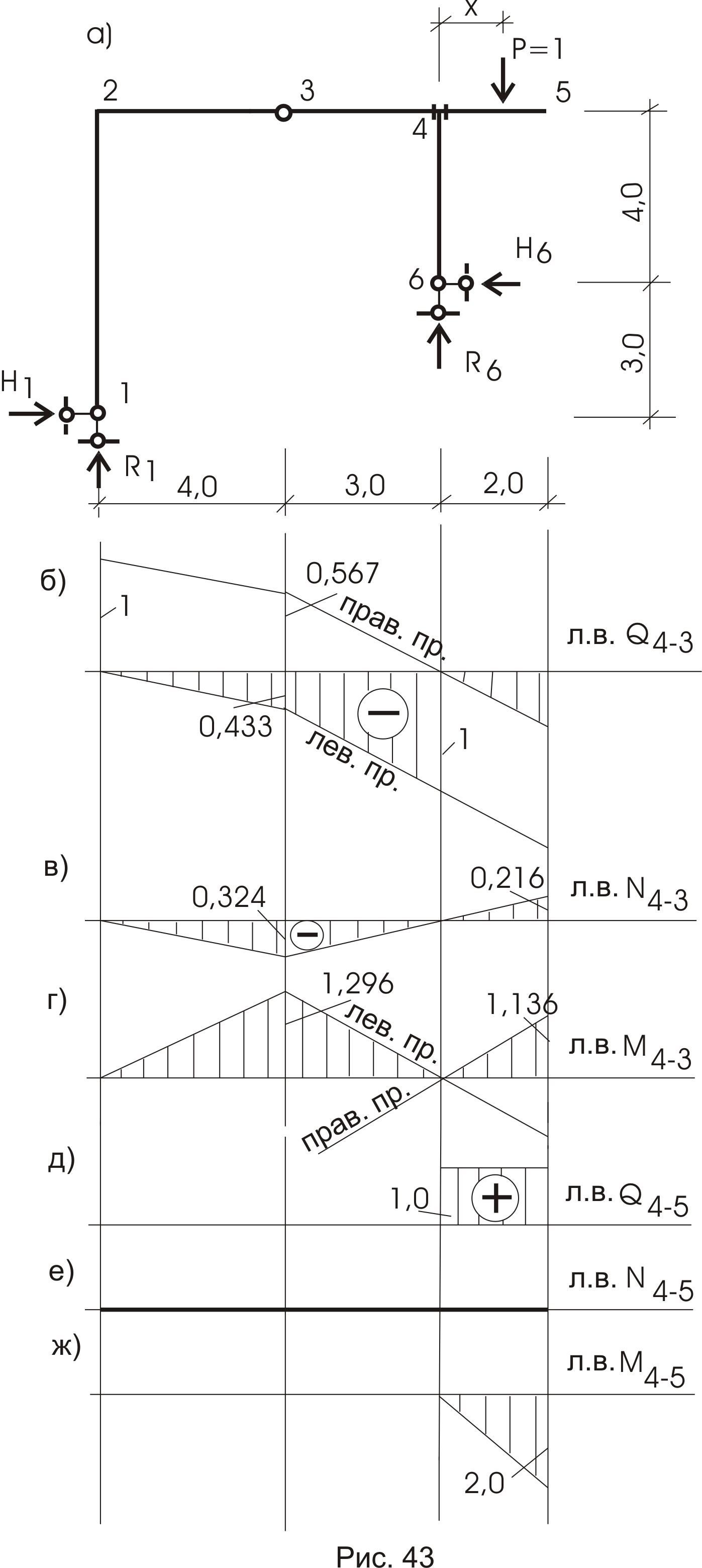
Сечение 4 на участке 4 – 3 – 2.

Линия влияния Q_4-3 (рис. 43б).

Величина перерезывающей силы в сечении 4 участка 4 – 3 – 2 ( ) будет зависеть от положения силы Р = 1.

Сила Р = 1 слева от сечения 4.

.

Получили так называемую левую прямую.

Сила Р = 1 справа от сечения 4 – 3.

правая прямая.

Линия влияния N_4-3 (рис. 43в).

Независимо от положения нагрузки Р = 1, величина N_4-3 будет равна либо Н₁, либо Н₆ , т. е.

.

Линия влияния М_4-3 (рис. 43г).

Сила Р = 1 слева от сечения: (левая прямая).

Сила Р = 1 справа от сечения.

Здесь возможны два варианта вычисления:

а) , т. е. ;

б) Силу Р = 1, находящуюся справа от сечения 4 стержня 4 – 3, зафиксируем ординатой х от узла 4 (рис. 43а). Тогда

или .

Линия влияния уже построена. Остается при х = 2 добавить к значению –0,864 величину 2, т. е.:

; ;

; .

Для усилий сечения 4 участка 4 – 5 линии влияния строятся как для консоли (рис. 43 д,е,ж). Предлагаем построить их самостоятельно.

Вычисление усилий по линиям влияния

Значение усилия может быть подсчитано от заданного вида загружения по линии влияния, построенной для этого усилия, по формуле:

,

где:

Р_i - величина сосредоточенной нагрузки;

i – порядковый номер нагрузки;

y_i - ордината линии влияния под силой Р_i ;

q - величина равномерно распределенной нагрузки;

_лв - площадь линии влияния на участке приложения равномерно распределенной нагрузки.

Обратимся к примеру (рис. 44)

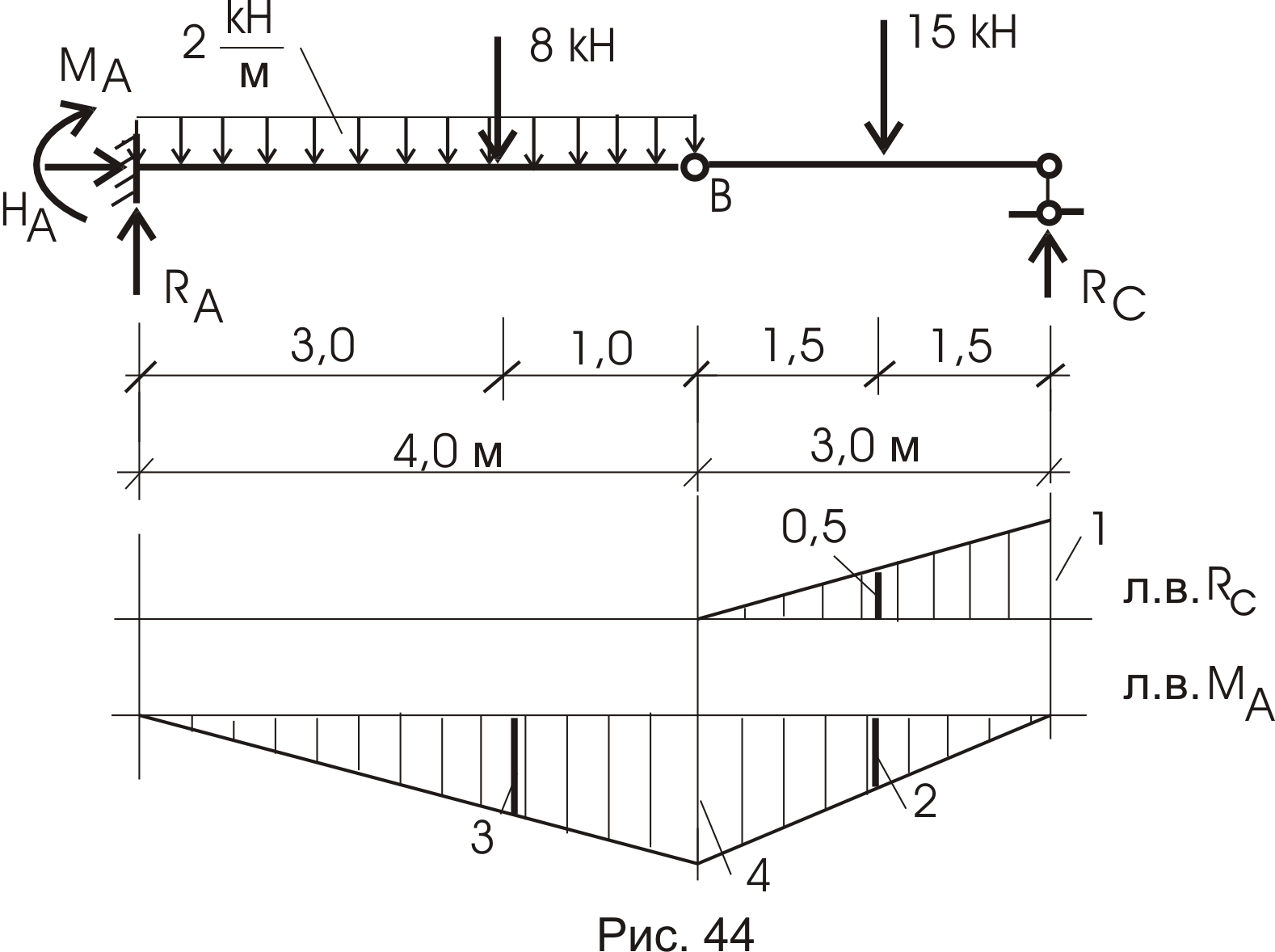
Вычислим величину реакции опоры С. Значение силы 15кн умножим на значение линии влияния под силой (0,5) и получим:

.

Для сравнения нетрудно подсчитать реакцию из уравнения: изгибающий момент в шарнире В правых сил равен нулю:

, откуда находим R _с = 7,5 кН.

Аналогично находим:

.

1.6 Определение перемещений

Перемещения точек конструкций и их элементов вычисляются по формуле Мора:

.

В выражении первые три слагаемые определяют перемещения точек от внешней нагрузки. Причем, из них учитываются для той или иной конструкции все три слагаемые (арочные конструкции) или одно слагаемое (ферма – слагаемое с N, рама – слагаемое с М).

Четвертое слагаемое в выражении определяет перемещения точек от осадки (перемещения) опор. И последние два слагаемых определяют перемещения точек от воздействия на конструкцию изменений температуры.

Рассмотрим по принципу независимости действия сил перемещения точек для различных конструкций от каждого воздействия отдельно.

Балки и рамные конструкции

Пример 1. Для балки, загруженной равномерно распределенной нагрузкой (рис. 45а), требуется определить:

1. Перемещение по вертикали точки К ( ).

2. Перемещение по вертикали точки 3 ( ).

3. Угол поворота точки 3 ( ).

Для нахождения этих перемещений воспользуемся первым слагаемым в формуле Мора, а именно:

.

Здесь М₁ – эпюра моментов от воздействия единичной нагрузки. Для первой задачи единичную нагрузку прикладываем в точку К по вертикали (рис. 45в); для второй задачи – в точку 3 по вертикали (рис. 45г); для третьей задачи единичную нагрузку в виде сосредоточенного изгибающего момента прикладываем к точке 3 (рис. 45д) ;

М_р – эпюра изгибающих моментов от заданной внешней нагрузки (рис. 45б);

EJ – жесткость балки при изгибе. Для нашего примера .

Интеграл вычисляется либо по правилу Верещагина, либо по правилу Симпсона.

Рекомендации:

- если обе эпюры прямолинейны, то удобнее вычислять интеграл по правилу Верещагина, т. е.

;

- если одна из эпюр криволинейна, то удобнее интеграл вычислять по правилу Симпсона:

.

Необходимо помнить: если одна из эпюр на участке интегрирования имеет излом (рис. 45 в), то нужно интегрирование на этом участке разбить на два участка (граница участков интегрирования – точка излома).

Определение .

Перемножим М_р на М₁ (рис. 45б,в).

Напоминаем правило знаков при перемножении: знак произведения положительный, если обе координаты эпюр моментов расположены по одну сторону от оси стержня.

Определение .

Перемножаем эпюру М_р (рис. 45б) на эпюру М₁ (рис. 45г).

Знак минус указывает, что перемещение точки 3 происходит вверх (а не вниз, как мы предполагали) на 7 единиц.

Определение .

Перемножаем эпюры моментов, показанных на рис. 45б и на рис. 45д. Тогда:

.

Пример 2.

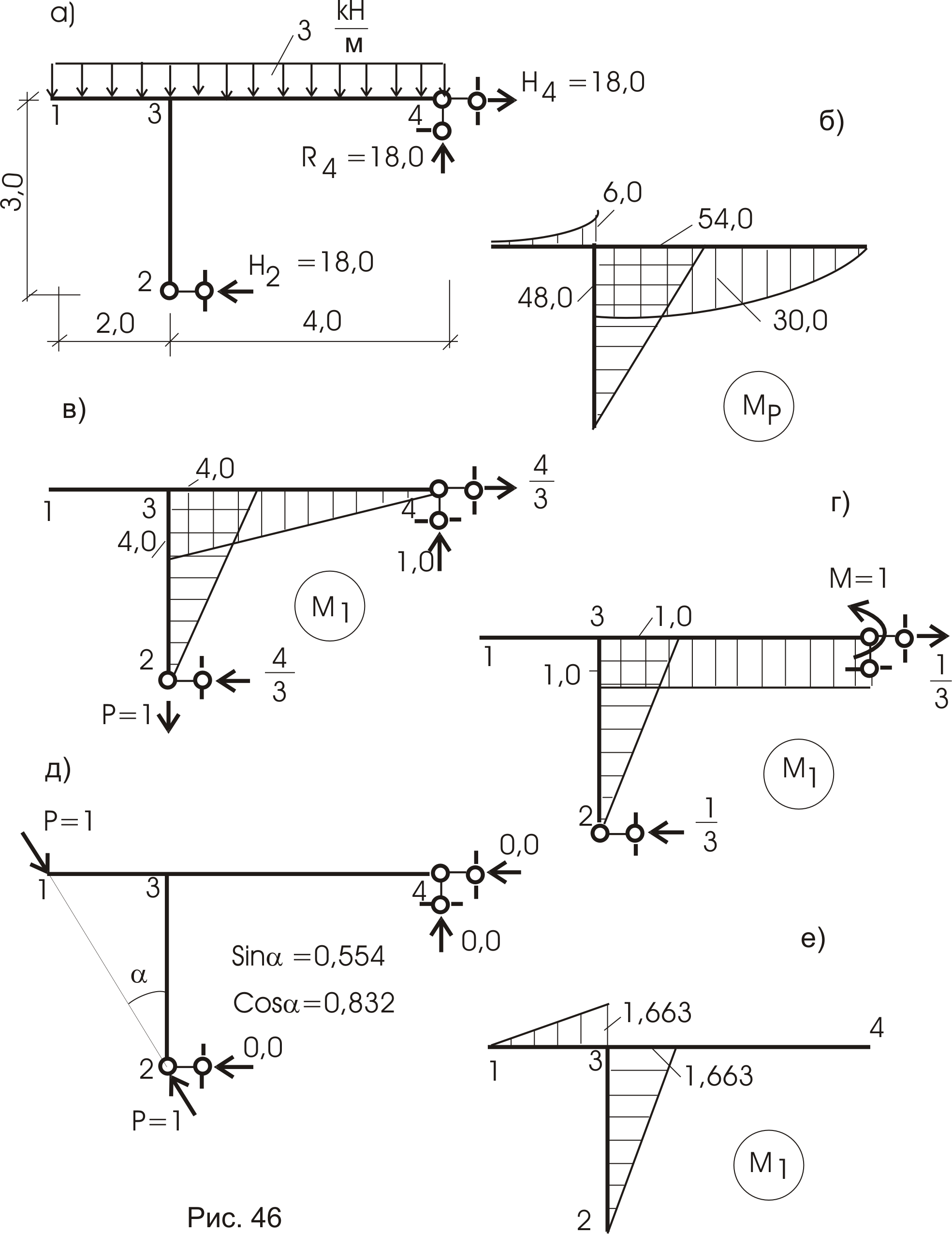
Дана рама (рис. 46). Требуется определить:

- вертикальное перемещение точки 2 ( );

- угол поворота сечения 4 ( );

- взаимное смещение узлов 1 и 2.

Для решения поставленных задач построим от внешней нагрузки эпюру изгибающих моментов – М_р (рис. 46б).

Задача 1. Определить вертикальное перемещение точки 2.

Строим эпюру M₁ от загружения точки 2 вертикальной силой Р = 1 (рис. 46в, здесь приложение силы и эпюра моментов от этой нагрузки показаны на одном рисунке).