1.5 Линии влияния
Линия влияния (л. в.) – это график изменения одного усилия (опорной реакции, реакции в связи, изгибающего момента, перерезывающего и продольного усилий) в определенном месте (сечении) конструкции от единичной безразмерной силы, которая движется по конструкции без ускорения, сохраняя при этом постоянное направление.
Линии влияния простых балок .
Рассмотрим простую балку на двух опорах (рис. 35а). Загружаем ее единичной силой Р = 1. Поскольку сила двигается по балке (скажем вертикального направления), то ее местоположение зафиксируем координатой х от опоры А.
Построим л. в. для опорной реакции RA.
Вычислим величину
RA,
рассмотрев уравнение статики
.
;
.
Из выражения RA видим, что величина опорной реакции меняется по линейному закону. Поэтому можно задать два сечения х и по этим величинам RA построить график изменения реакции RA.
При
,
.
При
(т. е. сила Р
= 1 будет
находиться на опоре В)
.
Откладывая эти значения RA на одном графике и соединяя их прямой (рис. 35б), получим л. в. RA в пределах длины балки. Когда сила Р = 1 будет находиться в точке С, величина RA может быть вычислена из подобия треугольников или аналитически из полученной ранее формулы:
.
Читателю предлагается самостоятельно построить л. в. Rb и сравнить с графиком, показанном на рисунке 35в.
Разберем построение л. в. для Мк. Сечение «К» на расстоянии 4.0 м от опоры А (рис. 36а).
Поскольку Р = 1 двигается по балке, то она может оказаться как слева от сечения «К», так и справа от него. Необходимо рассмотреть оба положения нагрузки относительно сечения «К».
а) Р = 1 слева от сечения «К» (как показано на рис. 36а).
Изгибающий момент в сечении «К» можно подсчитать как от левых, так и от правых сил. От правых сил момент подсчитать удобнее – меньше слагаемых (меньше сил):
.
Из этого выражения
следует, что
.
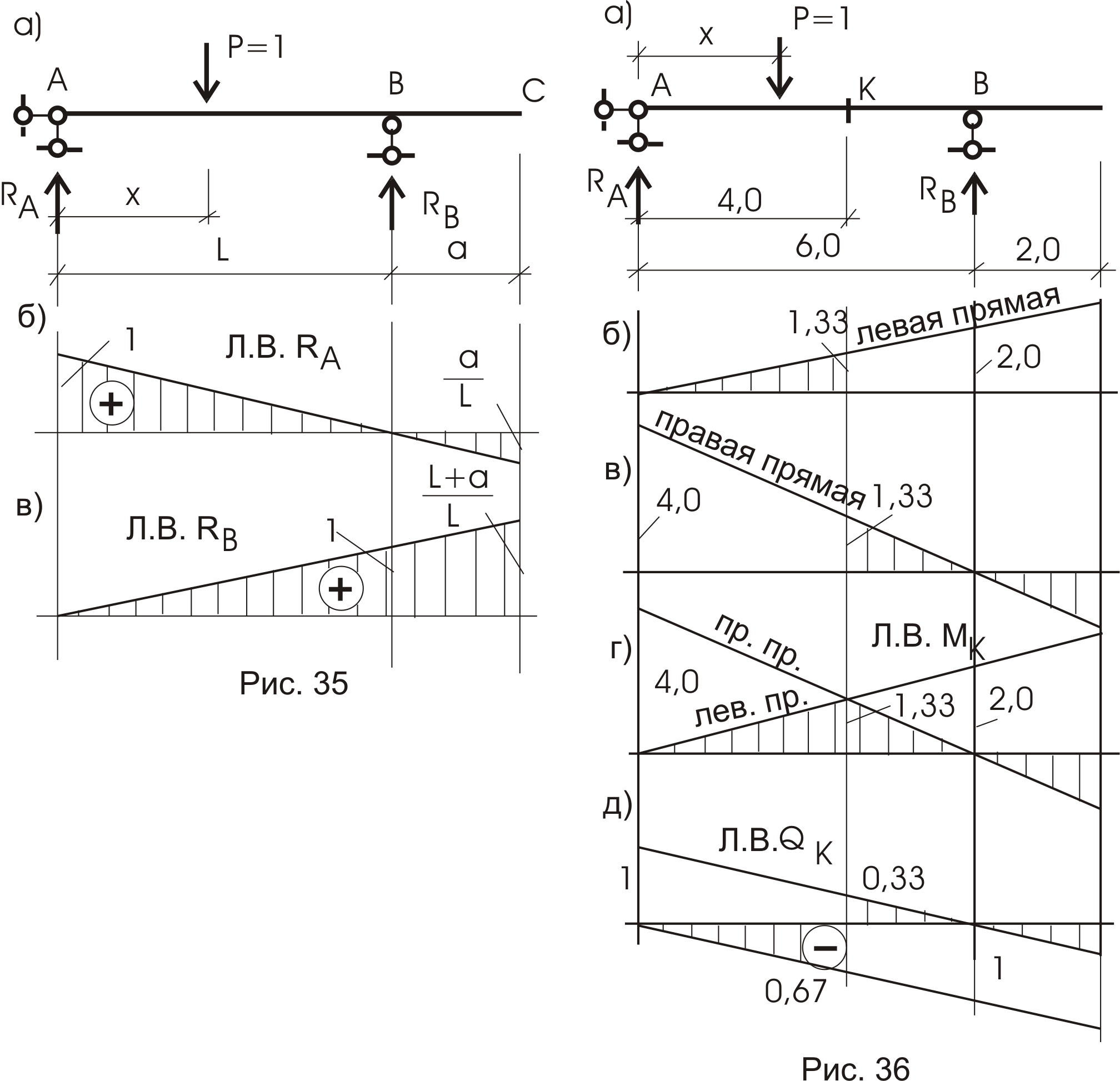
Следовательно, нужно построить л.в. Rb и все ее ординаты увеличить в 2 раза (рис.36б), но этот график будет справедлив только слева от сечения «К», т. е. там, где находится груз Р = 1. Эта прямая л.в. МК носит название – левая прямая. Рассмотрим второе положение Р = 1.
б) Р = 1 справа от сечения «К».
Момент в сечении удобнее подсчитать от левых сил (меньше сил на этой части балки):
или
,
т. е. следует построить л. в. RA , ординаты которой следует увеличить в 4 раза, и этот график будет справедлив только справа от сечения “К” – правая прямая л.в. МК (рис. 36в).
Для получения полного графика л. в. МК совмещаем на одной оси обе прямые (левую и правую) л. в. МК (рис. 36г).
По такому же принципу строятся и л. в. для QK (рис. 36д) и других усилий.
Рассмотрим консольную балку (рис. 37). Построим графики изменения (л. в.) опорных реакций и внутренних усилий в сечении «К».
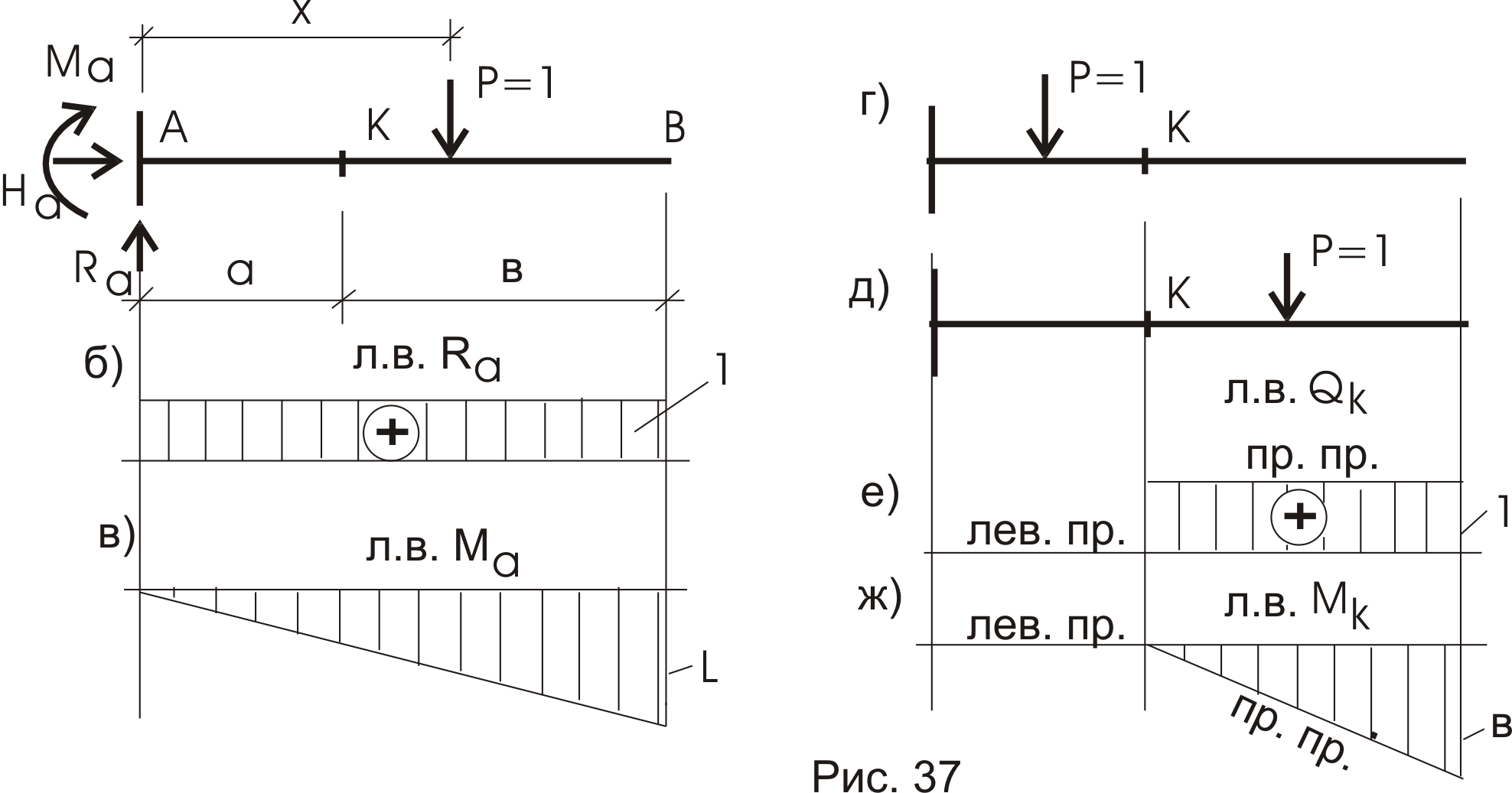
Линии влияния RA..
Реакция данной опоры определится из уравнения статики
; 
или
.
Обратим внимание - в уравнение не вошла координата х. Следовательно, реакция опоры А постоянная, где бы ни находилась сила Р = 1(рис. 37б).
Линия влияния HA..
Уравнение
дает, что
.
Линия влияния МA
Из уравнения
получаем, что
,
откуда
.
Знак минус говорит о том, что направление реактивного момента мы выбрали неверно, а само значение МА зависит от координаты х.
При
.
При
(где
l
– вылет консоли).
Линия влияния МА приведена на рис. 37в.
Линия влияния QK (перерезывающая сила в сечении К).
Рассмотрим положение груза Р = 1 слева от сечения (рис.37г).
Перерезывающую силу QK удобнее вычислить от правых сил, тогда
.
Левая прямая справедлива от заделки до сечения К (рис. 37е).
Когда груз Р = 1 окажется справа от сечения К (рис.37д), перерезывающую силу опять вычислим от правых сил:
.
Вновь заметим – величина QK не зависит от положения нагрузки на этом участке, т. е. QK – постоянная (рис.37е) и правая прямая справедлива от сечения К до конца консоли. В сечении К на графике л.в. наблюдается скачок на величину Р = 1.
Линия влияния МК (изгибающий момент в сечении К).
Подход к построению л.в. МК такой же, как и для QK. Предлагается проделать эти построения читателям самостоятельно и результаты сравнить (рис. 37ж).
Линии влияния усилий в ломаных стержнях (рамах).
Рассмотрим простейшую раму (рис.38). Будем считать, что Р = 1 двигается по горизонтальному стержню 2-3 и направлена вертикально.
Поскольку Р = 1 двигается по линии 2-3, то все графики строим по проекции этой линии (рис. 38).
Линия влияния Н1
Запишем выражение для определения Н1:
;
,
откуда находим
.
При
;
.
График изменения Н1 показан на рисунке 38б.
Линия влияния Н3
;
,
откуда
.
Знак минус указывает,
что направление выбрано нами неудачно.
Сменим его на противоположное. Другими
словами, величина
.
Линия влияния R3
: 
; 
.
Это означает, что величина реакции R3 не зависит от положения нагрузки (рис. 38в).
Линия влияния M21 (момент в сечении 2 участка 2-1)
Величину изгибающего
момента запишем как сумму моментов
нижних сил, т. е.
или величина момента меняется так же, как л.в. Н1, ординаты которой умножаются на 4 (м) (рис. 38г).
Линия влияния Q21 (перерезывающая сила в сечении 2 участка 2-1)
.
Уравнение говорит само за себя (рис. 38д).
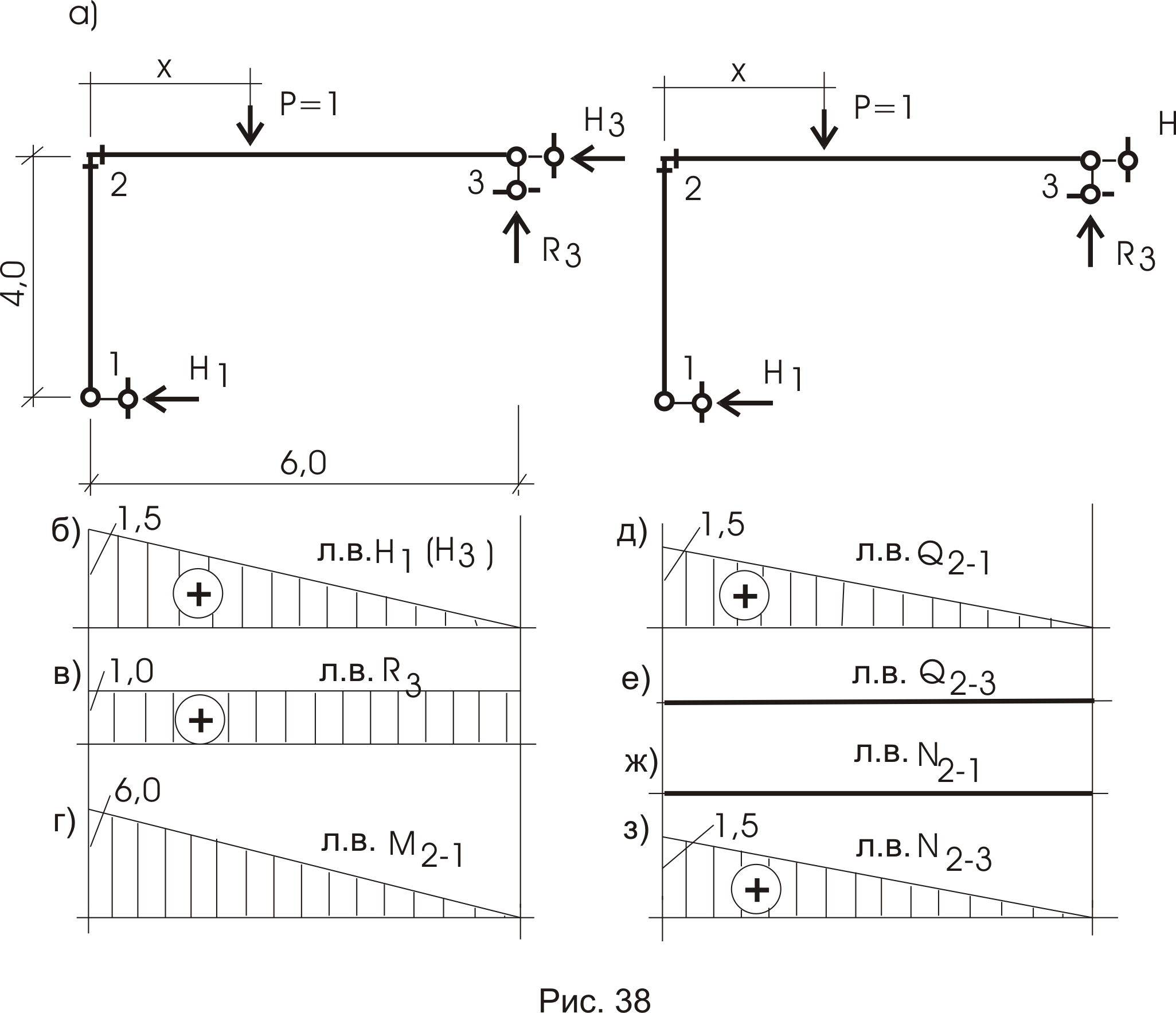
Линия влияния Q23 (перерезывающая сила в сечении 2 участка 2-3)
.
Здесь нужно считать, что сечение в узле 2 стержня 2-3 располагается бесконечно близко к узлу 2 (рис. 38е).
Линия влияния N21 (продольная сила в узле 2 участка 2-1) (рис. 38ж).
(из проекции на
ось стержня 2-1).
Линия влияния N21 (продольная сила в узле 2 участка 2-3) (рис. 38з).
(из проекции на
ось стержня 2-3).
Линии влияния усилий в стержнях фермы
Рассмотрим ферму (рис. 39). Построим л. в. для усилий стержней 2-ой панели, а именно: N2-9; N9-8; N2-8; N2-3 и N3-8. Линии влияния опорных реакций строим по аналогии с л. в. реакций простой балки. Груз Р = 1 движется по верхнему поясу (рис.39б,в).
Линия влияния N2-9.
Наметим путь определения усилия N2-9. Проведем сечение, разрезав стержень 2-9 (рис. 40).
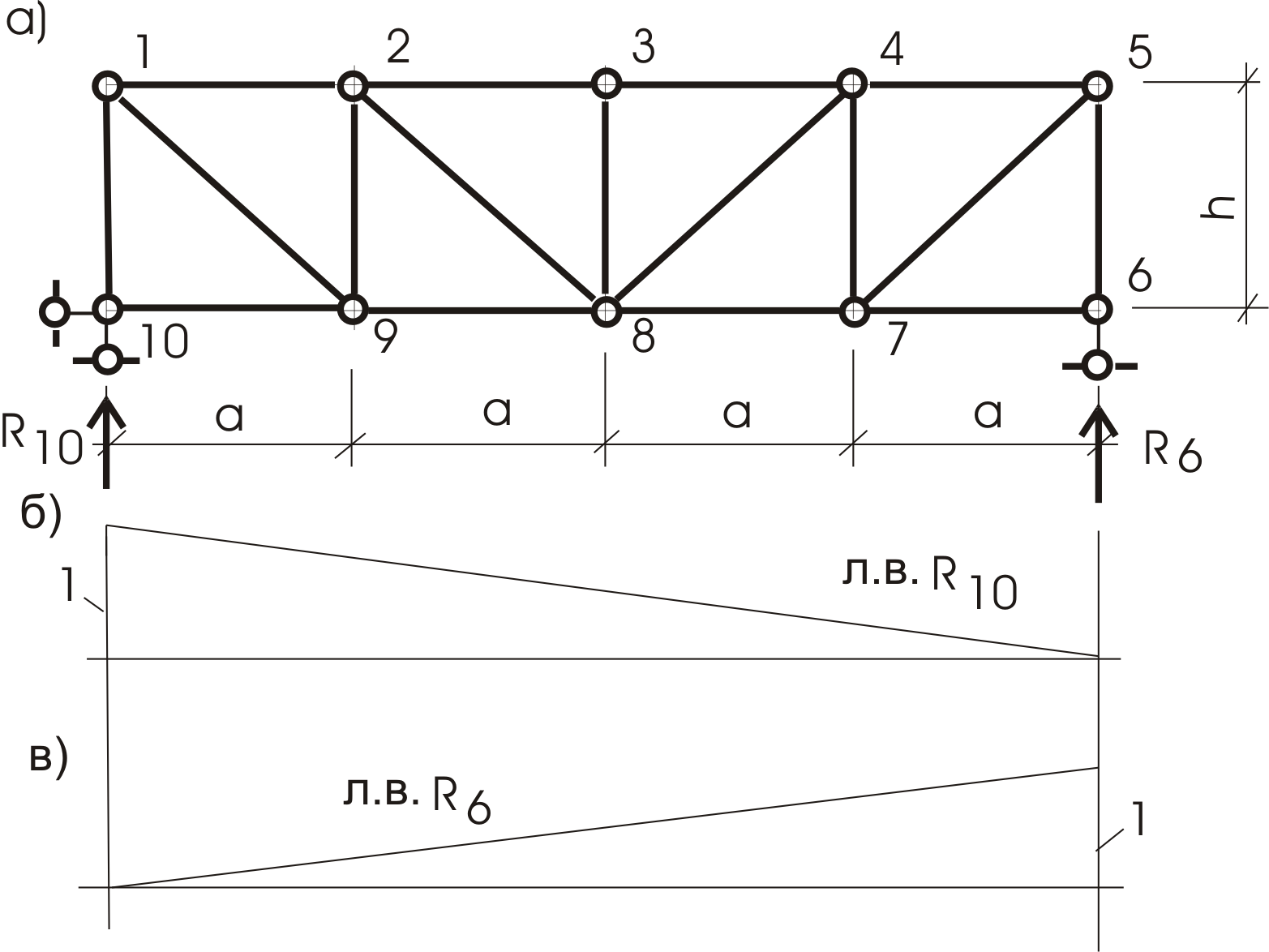
Рис. 39
Относительно этого сечения груз Р = 1 будет находиться слева и справа.
1) Р = 1 слева от сечения (на рисунке груз не показан).
Рассматривая правую незагруженную часть фермы, находим, используя одно из уравнений статики, усилие N2-9.
; 
или
.
Левая прямая справедлива при грузе в 1 узле.
2) Р = 1 справа от сечения 1 – 1 (правая прямая)
; 
;
(рассмотрели левую часть фермы – незагруженную).
.
Правая прямая справедлива от узла 2 до узла 5.
От узла 1 левой прямой до 2 узла правой прямой проводим передаточную прямую (рис. 40б).
Линия влияния N2-3.
Проведем сечение по стержням 2–3, 2-8, 9-8 и при нахождении усилия N2-3 будем пользоваться суммой моментов относительно узла 8.
а) Груз Р = 1 слева. Рассматриваем равновесие правой части.
; 
.
Отсюда 
.
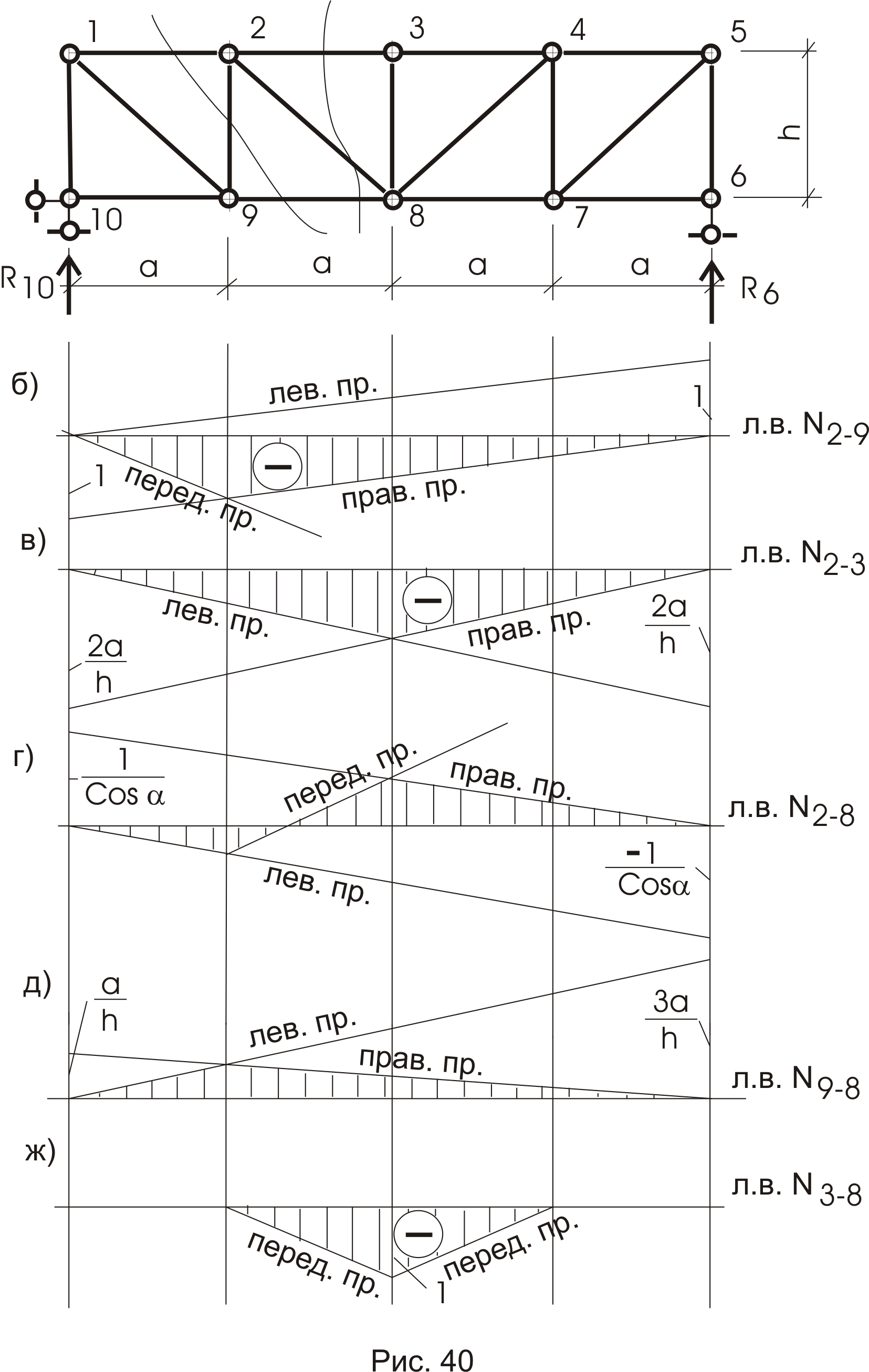
Линию влияния R6
мы увеличиваем в
раз (рис. 40в). Левая прямая справедлива
от узла 1 до узла 2.
б) Груз Р = 1 справа (правая прямая).
Рассматриваем равновесие левой части.
; 
или
.
Правая прямая (рис. 40в) справедлива от узла 3 до узла 5.
Между 2 узлом левой прямой и 3 узлом правой прямой проходит передаточная прямая, в данном случае совпадающая с левой прямой.
Линия влияния N2-8.
Используем уже проведенное сечение. В качестве исходного уравнения примем сумму проекций на ось «y».
а) Груз Р = 1 слева.
; 
.
Отсюда
(рис. 40 г).
График справедлив только от узла 1 до узла 2.
б) Груз Р = 1 справа от сечения.
; 
.
(рис. 40г).
Правая прямая
будет справедлива от узла 3 до узла 5.
От узла 2 левой прямой до узла 3 правой прямой проводится передаточная прямая. Отметим особенность: для раскосов передаточная прямая занимает положение, близкое перпендикуляру к данному раскосу.
Линия влияния N9-8
Для этого усилия
основным уравнением примем
.
а) Р = 1 слева (левая прямая)
; 
.
(рис. 40д).
б) Р = 1 справа (правая прямая)
, 
.
(рис. 40д).
Линия влияния N3-8 (рис. 40ж).
Для определения данного усилия воспользуемся вырезанием узла 3. Расположение стержней, сходящихся в узел 3, попадает под частный случай: если в узел сходятся три стержня, два из которых лежат на одной прямой, то при отсутствии нагрузки в этом узле усилие в отдельно стоящем стержне
(N3-8)
равно нулю. Следовательно, если сила
будет находиться в узлах 1, 2, 4, 5, усилие
.
Если узел 3 будет
загружен силой Р
= 1, то
.
От узла 2 до узла 8 и от узла 3 до узла 4 на л.в. N3-8 будут занимать место передаточные прямые (рис. 40ж).
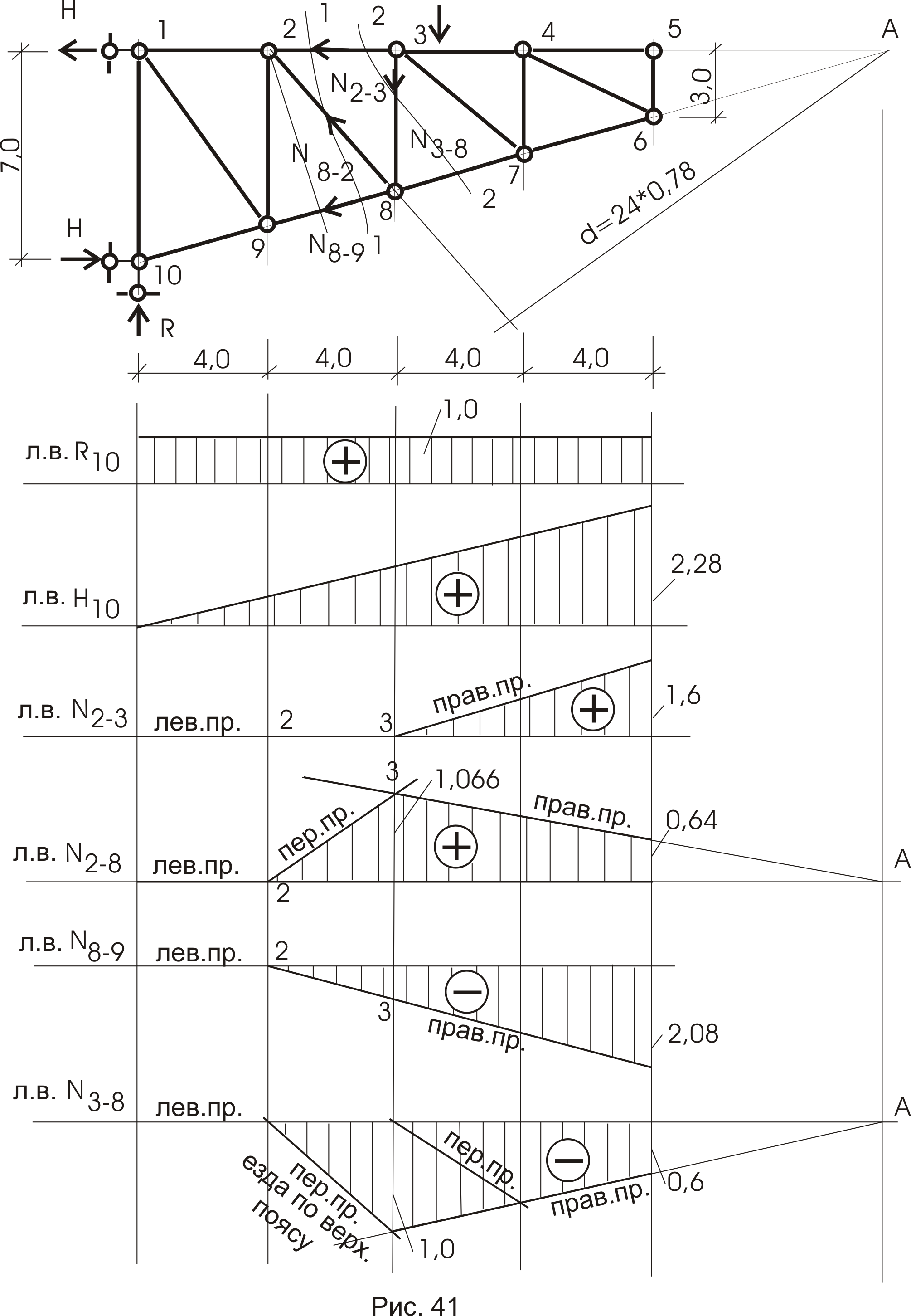
Далее читателям предлагается самостоятельно построить линии влияния для усилий в стержнях фермы и результаты сравнить с представленными решениями (рис. 41).
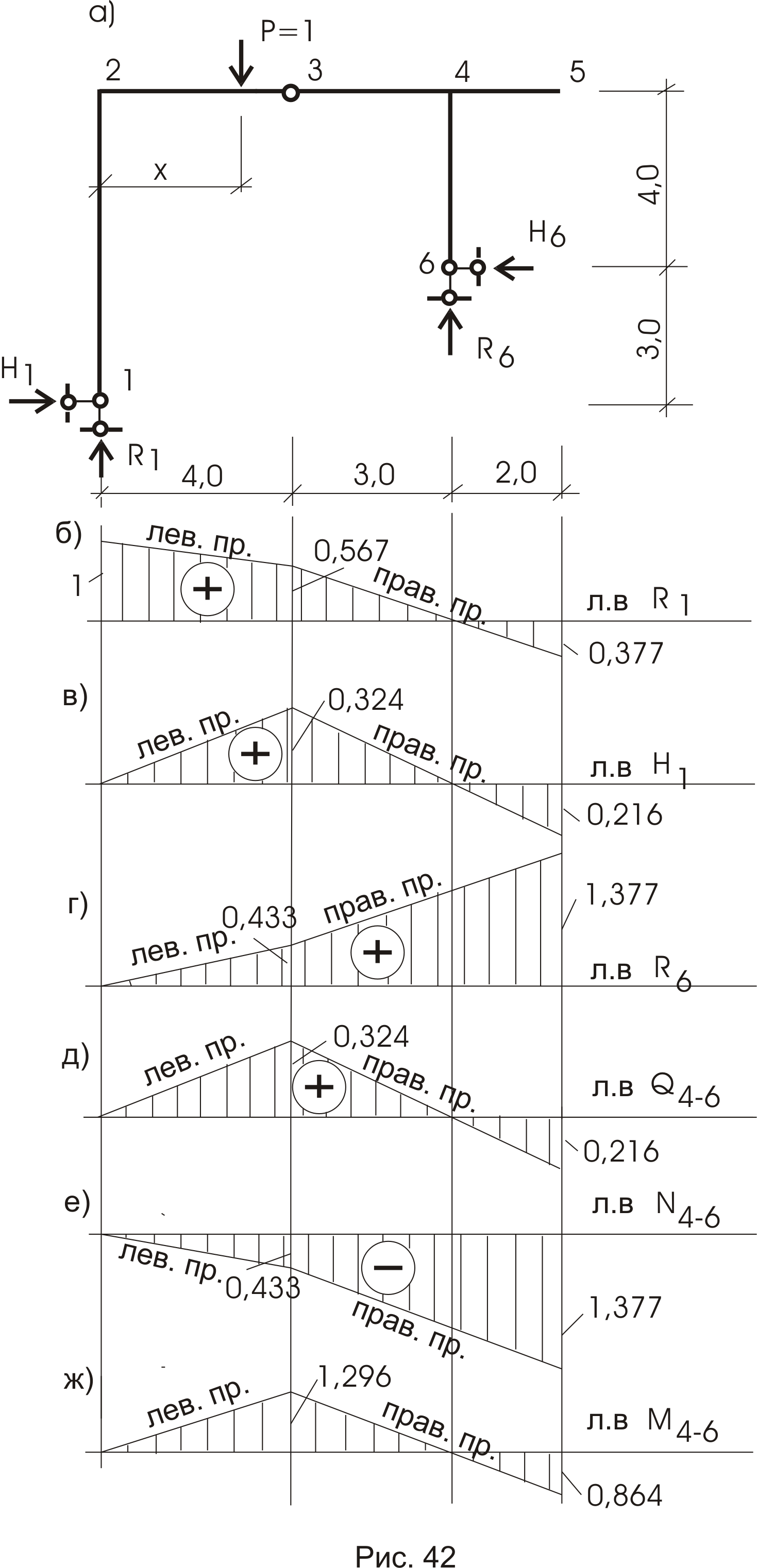
Линии влияния усилий в двухдисковой конструкции
Построения рассмотрим на примере двухдисковой рамы (рис. 42).
Линии влияния опорных реакций.
Линия влияния R1 .
Вычисляем опорную реакцию R1:
; 
.
При Р = 1 слева от шарнира 3:
; 
.
При Р = 1 справа от шарнира 3:
; 
.
Решение системы 2-х уравнений с 2-мя неизвестными при Р = 1 слева от шарнира 3:
;
;
дает
.
Придавая координате «х» крайние значения
на этом участке, получим величину R1:
при
,
.
При Р =1 справа от шарнира 3 получим систему двух уравнений :
;
,
решение которой
дает:
,
при
;
;
.
График изменения
смотрите на рис.42б.
Линия влияния Н1
Из полученных ранее уравнений при известном значении R1 находим величину Н1 :
При Р
= 1 слева от
шарнира 3
;
при
;
.
При грузе Р
= 1 справа от
шарнира 3
;
при
;
;
.
По полученным значениям линия влиянии Н1 построена на рисунке 42в.
Линия влияния Н6 .
Из общего уравнения равновесия конструкции:
; .
Откуда следует,
что
,
и следовательно,
(рис. 42в).
Линия влияния R6 .
Воспользуемся уравнением равновесия всей конструкции:
. 
.
Отсюда 
.
Линия влияния R6 показана на рисунке 42г.
Линии влияния внутренних усилий
Наметим сечения в узле 4 на стержне 4 - 6; в узле 4 на участке 4 - 3; в узле 4 на участке 4 – 5 (рис. 43а).